目录

一：思考方式

二：例题

例题1：数字三角形

例题二：最长上升子序列​​​​​​​

例题三：最长公共子序列

---

一：思考方式

线性dp就是一条线上的动态规划

二：例题

例题1：数字三角形

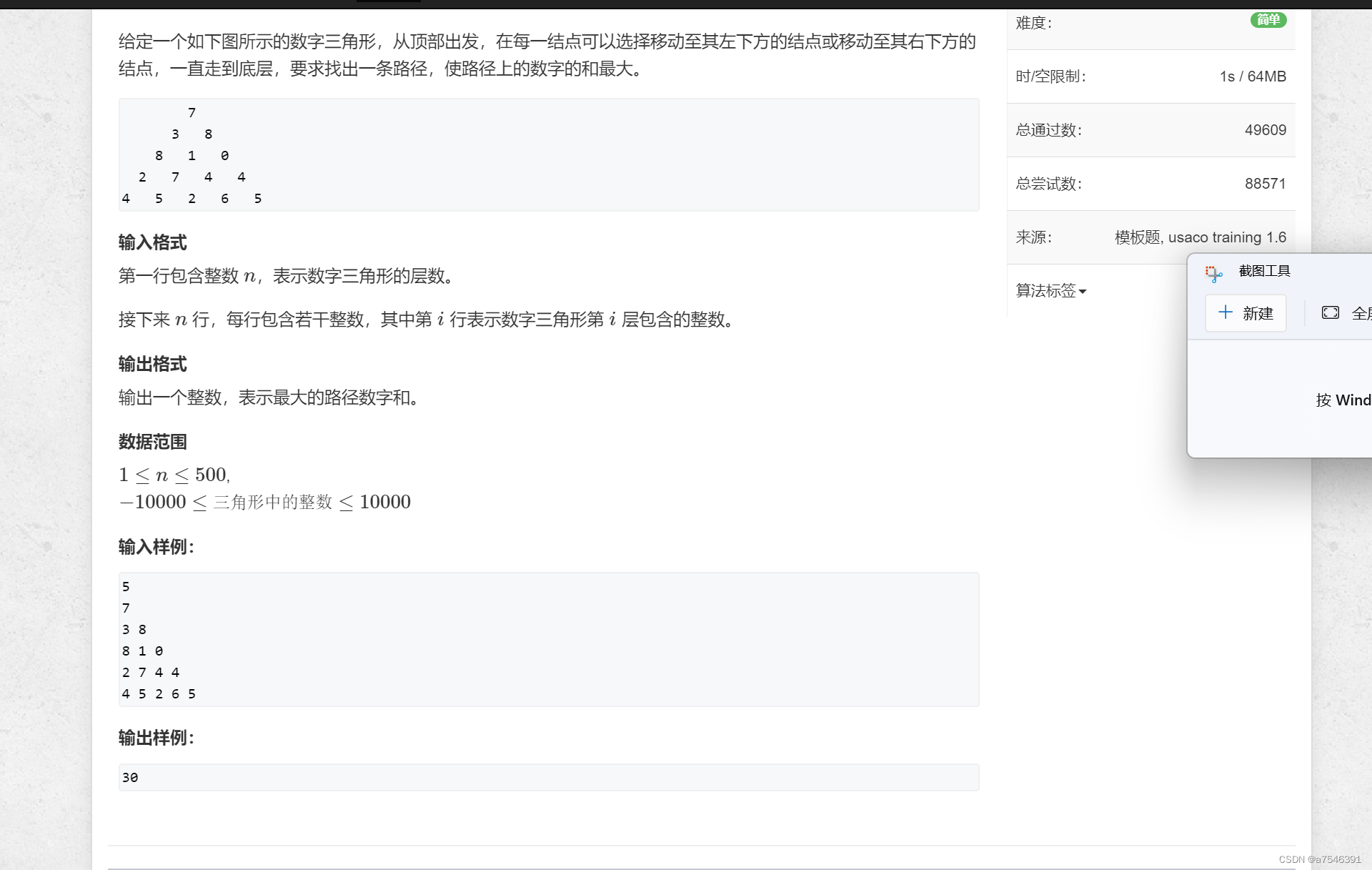
 状态表示：二维  f(i,j)  ,从起点到(i,j)的max路径 

状态计算：左上来的   f[i-1,j-1]+a[i,j]     右上来的   f[i-1,j]+a[i,j]       a[ ]为(i,j)的值

#include<iostream>
#include<algorithm>
using namespace std;
const int N=510,inf=1e9;
int f[N][N];
int a[N][N];
int n;
int main(){
    cin>>n;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=i;j++)
            cin>>a[i][j];
    
    //初始化为负无穷,为了确保全负数的路径正确，所以考虑将最左-1最右+1也要初始化为负无穷
    for(int i=1;i<=n;i++)
        for(int j=0;j<=i+1;j++)  //注意0---j+1，因为三角最左和最右也要判断 （即使最左的数没有左上，最右的数没有右上）
            f[i][j]=-inf;
    
    f[1][1]=a[1][1];
    for(int i=2;i<=n;i++)
        for(int j=1;j<=i;j++)
            f[i][j]=max(f[i-1][j-1]+a[i][j],f[i-1][j]+a[i][j]);
    //结果
    int res=-inf;
    for(int i=1;i<=n;i++)res=max(res,f[n][i]);
    cout<<res<<endl;
    return 0;
}

因为，本题状态更新时，在第一列会出现非法状态向合法状态转移的情况，所以要注意数组的初始化。由于本题有负数，所以只需要将数组中所有元素初始化成负无穷即可。

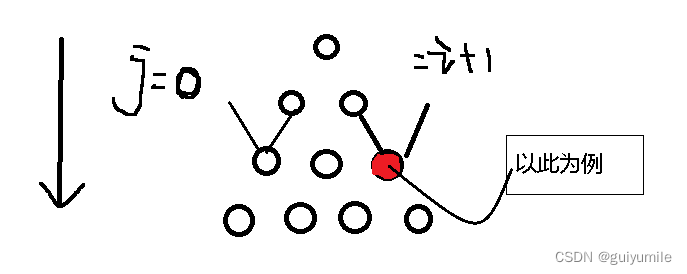
更好的解法，本题可以从下往上求解，从倒数第二行开始，这样左下右下不会有空的，那么就不用初始化了

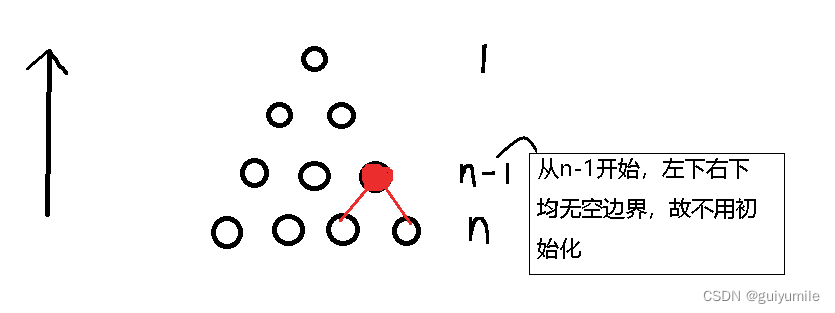
//不用考虑空边界，所以不用初始化为-inf

//
for （int i=n-1;i>=1;i--）{
	for(int j=1;j>=1;j--){
		f[i][j]=f[i][j]+max(f[i+1][j],f[i+1][j+1]);
	}
}
cout<<f[1][1]<<endl;

例题二：最长上升子序列

给定一个长度为 N 的数列，求数值严格单调递增的子序列的长度最长是多少。

输入格式
第一行包含整数 N。

第二行包含 N 个整数，表示完整序列。

输出格式
输出一个整数，表示最大长度。

数据范围
1≤N≤1000，
−10 ^ 9≤数列中的数≤10 ^ 9

---

输入样例：
7
3 1 2 1 8 5 6

---

输出样例：
4             （1、2、5、6）

时间复杂度：O（n2）

一：状态表示：一维dp[i]

我们让dp[i]表示为所有以a[i]结尾的严格单调上升子序列长度的Max值。

二：状态计算：

直接求dp[i]不好求，所以我们以a[ i ]结尾的序列的前一个数存在的情况进行分类

不存在倒数第二个数a[ j ] ，则长度即为1

存在倒数的数，则长度为dp[ j ]+1  （j=1,2,3，...，i-1）（是a[i]倒数的数且递增的数的集合的长度+a[i]自己长度'1'）

 dp[i]  = max(dp[i], dp[j] + 1)    

#include<bits/stdc++.h>

using namespace std;
const int N = 1010;
int a[N], dp[N];
int n;

int main()
{
    cin>>n;
    for(int i=1; i<=n; ++i) cin>>a[i];
    
    int res = 1;//最少的情况是只有一个元素，输出 1 即可
    
    for(int i=1; i<=n; ++i)
    {
        dp[i] = 1;//一开始只有a[i]一个元素
        for(int j=1; j<i; ++j)//遍历a[i]之前的元素
        {
            if(a[j]<a[i])
            {
                dp[i] = max(dp[i], dp[j]+1);//根据方程，两者取max
                res = max(res, dp[i]);//在状态计算过程中顺便更新答案
            }
        }
    }
    
    cout<<res<<endl;
    
    return 0;
}

还有个要注意的点，我们划分的某一类可能会不存在，如果a[j]>=a[i]则意味着我们当前分的这一类所有序列都是不合法的，无需考虑，因此我们在划分集合的时候要特殊判断一下该类是否存在（a[j]<a[i]才存在）递增子序列

二分法

例题三：最长公共子序列

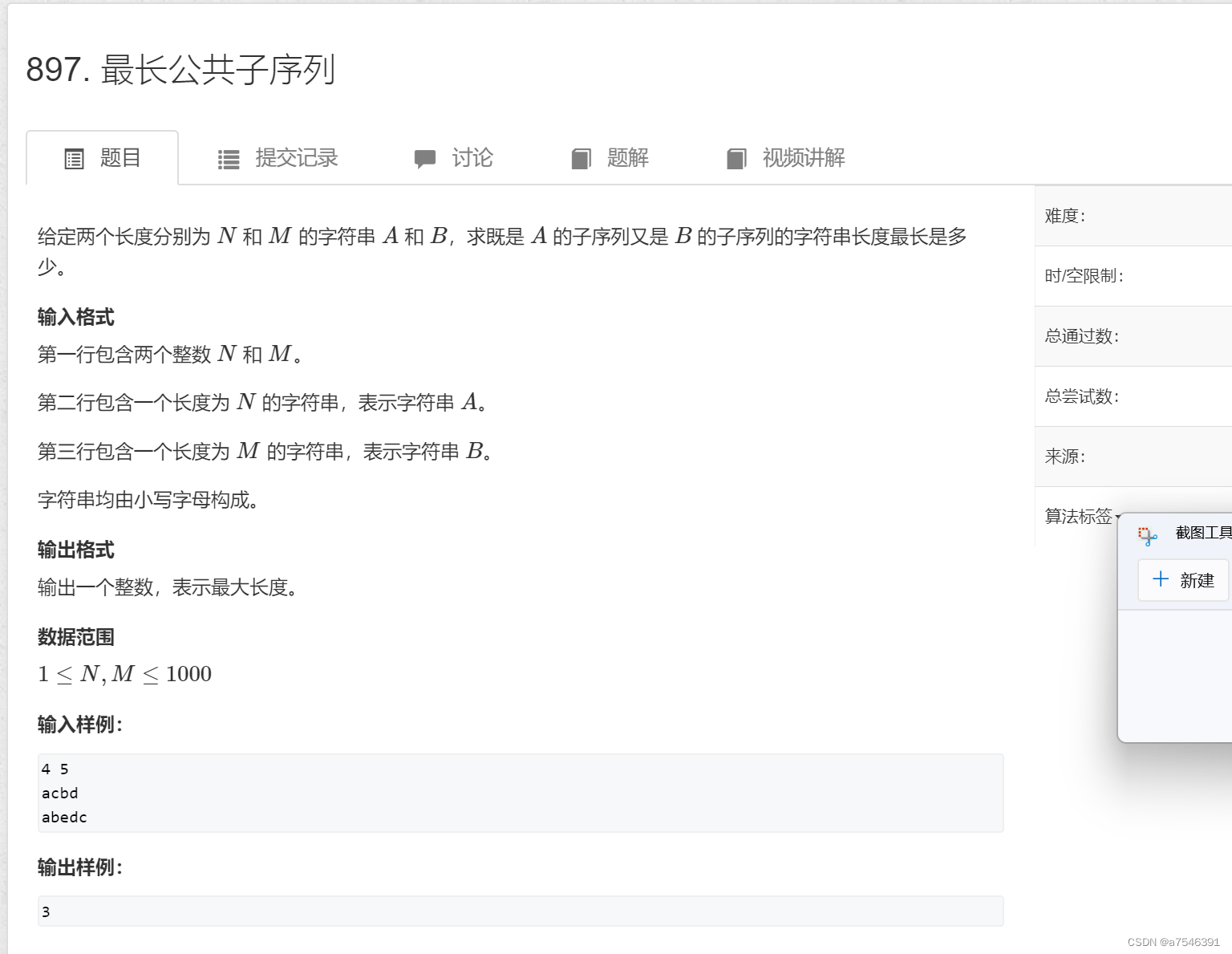
状态表示：f[i][j] 表示a[i],b[j]之前的最长公共序列
状态转移方程 ：集合的划分 ，划分依据就是a[i]与b[j]在不在相同的子序列中，

 

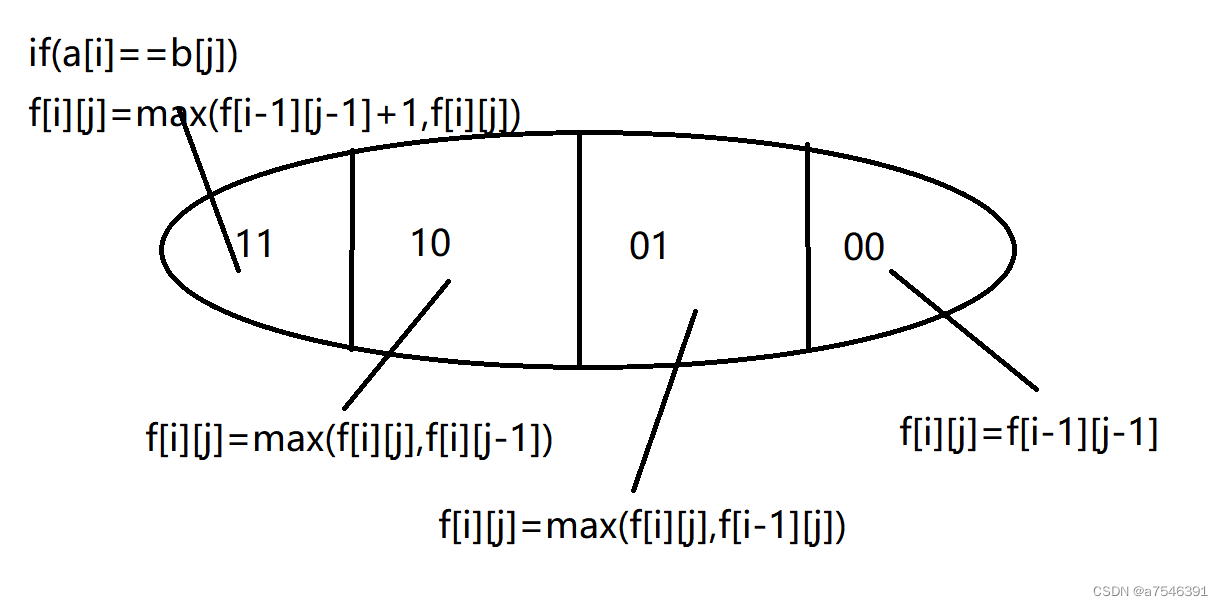
其中f[i][j-1]和f[i-1][j]与对应的（1，0）（0，1）其实是不等价的。f[i][j-1]代表a[i]，b[j-1]之前的最长公共序列，不一定包含b[j]。f[i-1][j]同理。
其中f[i-1][j-1]是包含在（1，0）（0，1）中的，所以可以去掉。
初始化，数组初始化时都为0。
 

#include<iostream>
#include<cstring>
using namespace std;
const int N=1100;
char a[N],b[N];
int n,m;
int f[N][N];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int j=1;j<=m;j++) cin>>b[j];
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            if(a[i]==b[j]) f[i][j]=max(f[i][j],f[i-1][j-1]+1);
            else f[i][j]=max(f[i-1][j],f[i][j-1]);
        }
    }
    cout<<f[n][m];
}