说在开头:关于第六届索尔维会议(2)
爱因斯坦一天都挺开心的,反正难题出给了玻尔,他还在自己的房间里拉起了小提琴,有人说爱因斯坦小提琴拉的跟锯木头一样,那也不至于那么夸张,但是水平业余应该是真的;他和玻尔的房间正好是上下楼,脚步声都能听见,爱因斯坦心中暗爽,玻尔今天晚上肯定失眠了,脚步声一直没停,还在屋子里来回溜呢。
第二天,出乎爱因斯坦意料的是,玻尔精神抖擞,这家伙是不是想出啥破解之道了?果然,玻尔上台也画了一个图,跟爱因斯坦的图差不多,也是一个方盒子,边上开了一个闸门,由一个机械钟控制。跟爱因斯坦图片不一样的是,盒子挂在一个弹簧秤下。爱因斯坦不是说可以测量到盒子质量的变化来计算光子的质量么?不能空口说白话啊,总要有测量工具吧?画个弹簧秤很合理的吧。在玻尔看来,在微观世界里,测量方式至关重要。
好,我们开始了:钟控制闸门打开,光子就飞了出去,箱子就瞬间变轻了;盒子挂在弹簧秤上,钟挂在盒子上是一体的。整个盒子带着钟的质量一变轻,弹簧秤就收缩了,拉着盒子往上那么一飘。别小看这微小的移动,在此过程中,根据爱因斯坦的广义相对论,箱子在地球引力场里面移动,会产生红移,时间会变慢,箱子上那个表的读数就会变慢(如之前分享广义相对论所说,引力场会对时间造成影响)。按照玻尔的计算,一个光子飞出箱子的一瞬间,箱子一轻,就被弹簧秤的弹簧往上一拽,在拽的过程中时间变了,那么把这个变化考虑进去,测不准原理就是正确的。
这下轮到爱因斯坦魂不守舍了,这实在太出乎意料了。爱因斯坦憋了三年的大招被玻尔一个晚上给破解了,而且是漂亮的玩了一招以其人之道还之其人之身:相对论、引力红移是爱因斯坦的成名绝技,万万没想到会在这方面出了纰漏。
玻尔是最坚决的革命派,他思想深远,穷幽极渺,却又如大江奔流,浩浩荡荡奔腾不息。物理学的未来只有靠量子。新世界不再有因果性,不再有实在性。上帝真的掷骰子,随机性是世界的基石,当电子出现在这里时,它是一个随机过程,并不需要有谁给它加上难以忍受的条条框框。爱因斯坦失望地看着这个场面,发展到如此地步实在出乎他所意料,失去了严格的因果性,世界将一片混乱。他现在知道量子论的根基比想象的要牢固的多,看起来量子论不太可能是错误的,或自相矛盾的。(参考自:曹天元-上帝掷骰子吗)
一,反激拓扑变压器
我们知道离线式电源拓扑是有三种基本电源拓扑衍生而来,一般小功率(<100w)的反激式电源拓扑是用多绕组电感器(即,变压器,但与正激变压器作用有所不同)替代常规单绕组电感器的升降压电源拓扑;而大功率正激变电源拓扑则是用变压器替代常规电感器的降压电源拓扑。
——在反激变换中的变压器,既有隔离的作用,也有储能的作用(同基本电源拓扑的电感器);而在正激变换中的变压器只提供隔离,储能由后端的电感器实现。
无论是正激还是反激电源拓扑,变压器都有一个重要的作用:由匝数比决定固定降压比。那对于升降压电源拓扑来说,从理论上来说其可以随意升压或降压到任何电平,为什么还需要变压器来变压呢?
1. 输入电源电压和输出电源电压压差非常大(举个栗子:输入380V,输出3.3V),那么其占空比将非常小(Ton<1%),减去“死区时间”后就可能没有导通时间Ton了;
2. 输入输出电压差太大,严重影响开关电源转换效率。
1,反激电源拓扑变压器功能
如下左图所示,反激式电源拓扑与升降压电源拓扑的相同点:所有输出的能量均先由电感器/变压器储能,再有电感器/变压器将收集的能量输出。两个阶段完全分开,即:没有直接从输入电源到输出电源的能量传递路径(关于不同电源拓扑能量传递,后续章节具体分析),所以需要更大尺寸的电感器/变压器。具体到变压器设计,下左图所示变压器原副边匝数比n = Np/Ns,其中Np为原边绕组匝数,而Ns为副边绕组匝数,图中有“圆点”的一端为同名端,电压极性分析相同,所以异名端(圆点对应非圆点端)电压极性相反。这是因为两组绕组绕在同一个磁芯,由于外部电流产生了磁通量,对于磁芯来说原副边绕组是等价的,都会产生感应电压,其感应电压的强度和极性由绕组匝数和绕线方式决定(变压器的具体原理,请复习:《电感器分类》)。
——对于变压器来说,同名端和异名端只是定义原副边绕组的输出电压极性,在设计中并没有固定同名端要电源或GND,变压器原副边的同名端和异名端可以同时切换,只需保证输出拓扑正确。
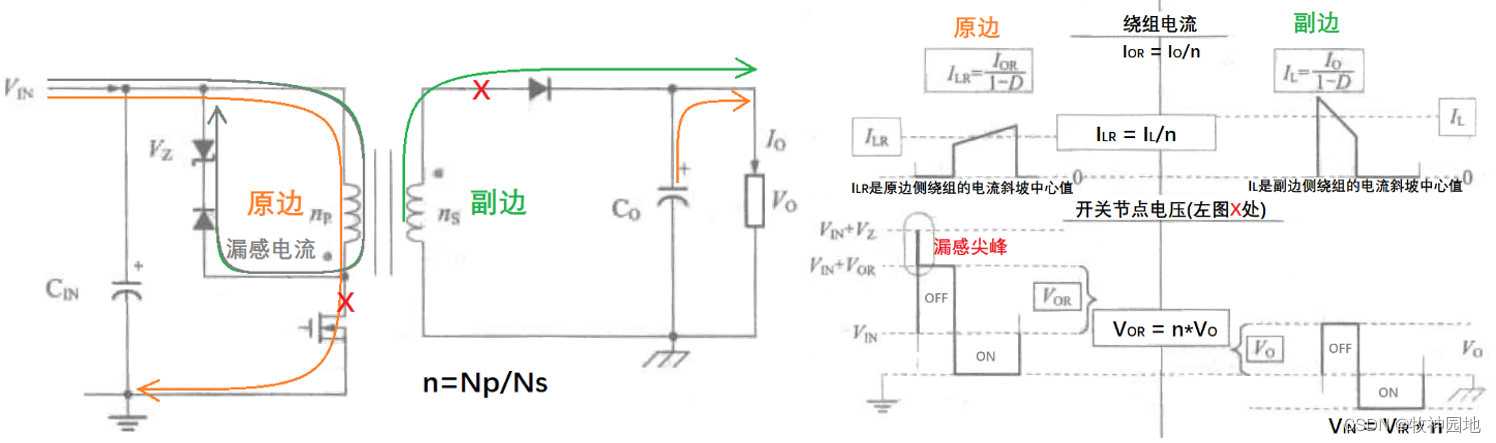
对于一般变压器来说,变压器的原副边绕组匝数(Np/Ns)比决定了原副边绕组的电压和电流之比,这是基于变压器原副边同时工作时Pin = Po推理出来的。但从电磁感应原理来说,原副边绕组匝数比决定的是原副边电压之比,与绕组中是否有流过电流无关(具体请参考:《电感器分类》中的推理过程)。对于反激电源拓扑,我们首先需要明确这一点。
如上图反激电源拓扑变压器工作原理,图中X为电源拓扑交换节点(即:电感器、开关管和二极管交接处,由于变压器的作用,原副边同名端等价,所以交换节点出现在两个地方):
1. 在变压器原边开关管导通时(异名端电压大于同名端电压),副边绕组无电流通过(异名端电压大于同名端电压):
1, 变压器原边电流不断增大,变压器磁芯储能增加;
2, 变压器副边电流为0,不消耗磁芯能量;
——此时变压器原边与副边与匝数比无关。
3, 原边开关管Vds电压为0(理想情况下,忽略导通电压);
4, 副边二极管左侧电压为负,根据变压器电压变换原理VIR = (-VIN)/n。
2. 在变压器原边开关管关断时(同名端电压大于异名端电压),副边绕组电流输出给负载(同名端电压大于异名端电压):
1, 理想情况下变压器原边绕组在开关管断开后没有电流流过,全部电流均由副边流出(变压器实现能量从原边向副边的传输);
——但变压器漏感(原副边绕组漏感,电路电感等)的存在,漏感电流通过钳位二极管消耗掉。
2, 变压器副边电流输出给负载和滤波电容器,磁芯储存的磁场能量转化为电能;
3, 原边绕组同名端电压上升,其电压根据变压器电压变换原理:VOR = VO*n,所以开关管漏极电压Vd = VIN + VOR;
——考虑变压器漏感,会产生一个电压尖峰(其能量不能通过副边消耗掉)VIN+VZ,通过二极管泄放。
4, 副边二极管左侧电压为正,电压被二极管钳位在Vo(忽略二极管压降)。
3. 根据如上过程分析,得到如下结论:在开关管导通阶段,原边绕组决定了所有绕组电压(原边绕组电压固定,有电流流过),而在开关关断阶段,副边绕组决定了所有绕组的电压(副边绕组电压固定,有电流流过);
——还是需要再次强调:对于变压器的磁芯来说,并无原边或副边的优先权或差别,它储存的能量等价的作用于原边和副边绕组上。
4. 虽然反激电源拓扑的原副边电流不是同时流过,但是原边在开关管导通时流过的电流ILR,与副边在开关管关断时流过的电流IL是有比例关系的;其与变压器原副边绕组的匝数比成反比,即:ILR = IL/n,其核心是变压器能量传输的平衡。
——原边绕组在开关导通时通过电流存储在变压器磁芯的能量:Ein = (1/2)*Lp*I²LR,在开关断开时输出给副边负载:Eo = (1/2)*Ls*I²L,在理想情况下Ein = Es,(1/2)*Lp*I²LR = (1/2)*Ls*I²L,ILR/IL = √(Ls/Lp)可得,我们知道L与匝数N²成正比,所以 ILR/IL = Ns/Np = 1/n;同时可以得到:ILR*n = IL,即原副边的安匝数相等(安匝数即是变压器的磁通Φ,有需要的同学请复习:《电感特性原理》)。
5. 对于变压器参数的计算规则:已知原边绕组电压求副边绕组电压,需除以匝数比(相反已知副边电压求原边电压要乘以匝数比);而电流的规则刚好相反,已知原边绕组电流求副边绕组电流,需要乘以匝数比。
——通过变压器的电压、电流转换,可以将隔离电源拓扑等效并套入基本电源拓扑进行计算和分析。
1.1 反激拓扑直流传递函数
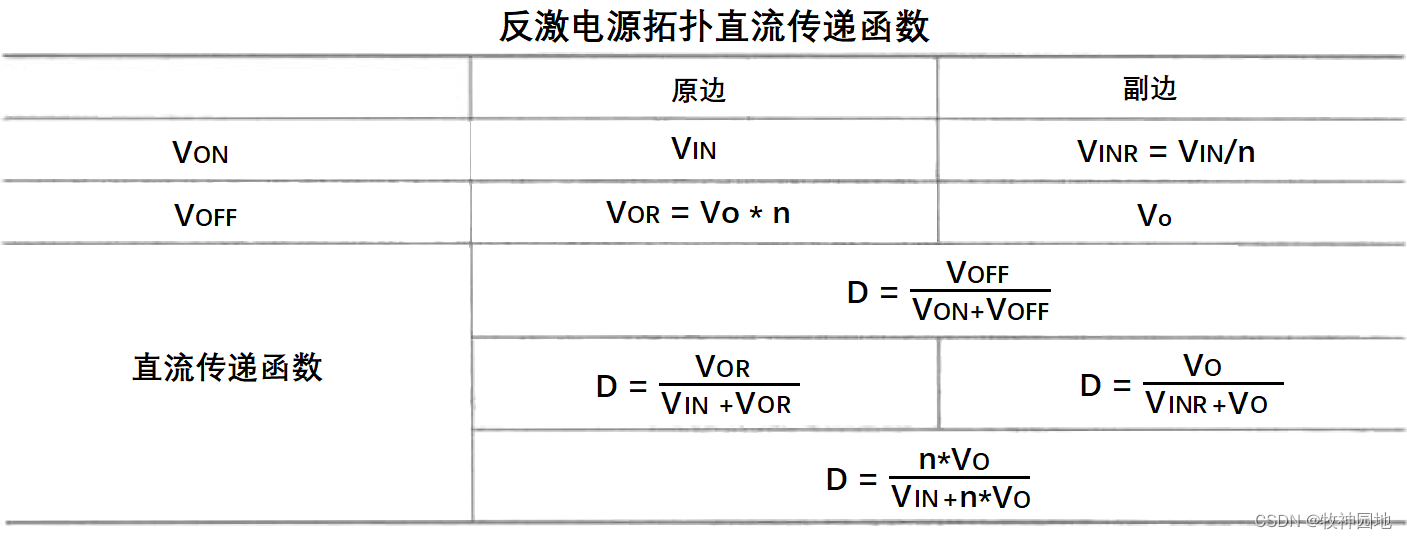
根据伏秒定律,我们可得对于任何拓扑的直流传递函数:D = Voff/(Von+Voff);可根据从原边或则副边进行计算(通过匝数比换算),得到最终的反激电源拓扑直流传递函数:D = n*Vo/(Vin+n*Vo)。
2,等效BUCK-BOOST拓扑模型
如果我们通过变压器的匝数比,用等效电流、电压的方式转换成传统BUCK-BOOST电源拓扑,即将反激电源拓扑的变压器简化成BUCK-BOOST电源拓扑的电感器,这将对电感器能量、输出滤波电容器、开关管以及二极管参数的计算带来方便。
等效BUCK-BOOST模型,其本质上是将隔离变压器的一侧电压和电流折算到另一侧,但是占空比一样,有两种折算方法:
1. 所有变量从副边侧折算到原边侧,输出电压/电流要乘以/除以匝数比;例如,输出电压为Vo,那么将输出电压折算到原边侧:VOR = Vo*n;
2. 所有变量从原边侧折算到副边侧,输入电压/电流要除以/乘以匝数比;例如,输入电压为VIN,那么将输入电压折算到副边侧:VINR = VIN/n。
对应折算关系如下图所示,举个栗子:有个反激电源输出功率为50w(5V/10A),匝数比为20,可得Vor = 5*20 = 100V,如果我们将输出电压/电流改为10V/5A,匝数比减小到10,那么Vor还是100V,对于原边电压/电流波形没有任何的变化,而且输出功率保持不变,开关电源原边侧不会知道其差别,我们可以从原边侧等效看成一个BUCK-BOOST电源拓扑:输入电压为Vin,输出电压为Vor,负载电流为Ior。同理我们可以从副边侧等效成BUCK-BOOST电源拓扑。
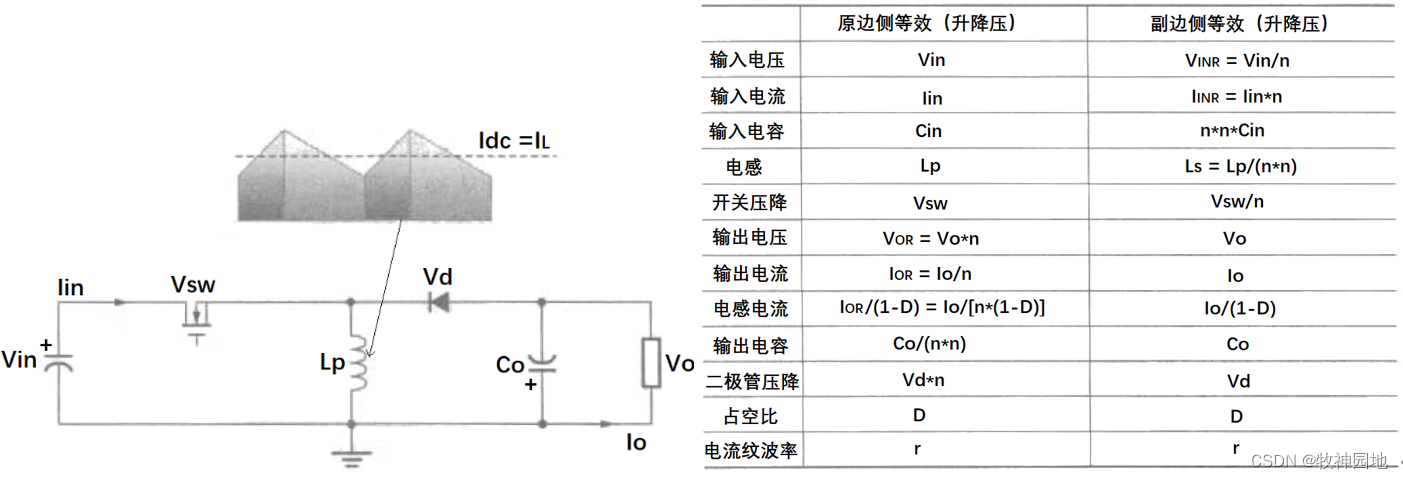
1. 从能量角度来理解原副边侧的电抗元件折算,假设反激电源拓扑中的输出电容Co被充电到Vo,储存的能量E =(1/2) *Co*V²o,折算成BUCK-BOOST电源拓扑,Vo转换成Vor = Vo*n,因此为了保持储能保持不变:E = (1/2)*(Co/n²)*(Vo*n)²,Co必须折算到原来的1/n²;
2. 反激电源拓扑与等效BUCK-BOOST电源拓扑的电流纹波率完全相同:副边侧电感器电流斜坡中心值(IL)必然等于Io/(1-D),将副边电感电流折算到原边后,斜坡中心值为 ILR = IL/n,也等于IOR/(1-D),而IOR = Io/n,可得电流纹波率同样都为r。
2.1 变压器漏感
在这理想等效过程中,有一个重要因素被我们所忽略了,那就是:反激变压器的漏感;由于变压器的原副边之间,还有一部分的磁场能量未能相互耦合形成有效的能量传输。原边侧开关管关断瞬间变压器原边电感能量可以通过副边的负载释放,但是漏感能量无处可去,因此会产生巨大电压脉冲尖峰(电感本身特性,具体在:《电源变换器基础》有介绍),造成开关管损坏。
——磁芯的磁阻很小,大部分磁通量是通过磁芯的,但还有很小一部分磁场是在空气中,这部分能量并不能从原边传递给副边,造成了漏感(具体原理参考:《电感器分类》中变压器部分);另外PCB板上的走线和变压器管脚寄生电感也是漏感的一部分(但大部分都在变压器的原边绕组中)。
由于这些漏感能量不能传输到副边,而且放任不管的话还会造成破坏,那么就只有两种选择:1,设法回馈至输入电容;2,设法将漏感能量消耗掉。一般简单处理方案是选择后者:直接采用稳压管钳位的方法(如第一节拓扑描述),将稳压管与二极管串联后并联在原边绕组上,或则直接将稳压管跨接在交换节点与原边侧地之间。
漏感既然是变压器本身的特性,那么有原边侧漏感(LLKP)也必然也存在副边侧漏感(LLKS),而变压器的总漏感(LLK)不仅是原边侧漏感(LLKP),还受到副边侧漏感(LLKS)的影响。按照定义,副边侧漏感不应该耦合到原边去:在开关管关断过渡过程中,原边侧漏感会阻碍原边侧电流续流输出,而所有副边侧电感也会阻碍副边侧电流流过续流通路;直到副边侧电流的续流通路真正建立起来,原边侧电流仍需通过某种途径续流,于是原边侧电感电流以稳压管钳位电路为续流同步。所以即是原边侧漏感为0,也会产生电压脉冲尖峰,副边侧漏感产生的影响与原边侧漏感相同。
——副边侧漏感阻碍副边续流通路的建立,那么磁芯的磁场能量必然会对原边侧施加感应电压,使之续流通路持续。
考虑副边侧漏感的影响可以计算变压器总漏感:LLK = LLKP + n²*LLKS。与其它电抗元件一样,副边侧漏感按匝数比的平方折算到原边侧,与原边侧漏感串联相加。所以:如果变压器匝数比很大,那么变压器副边漏感折算到原边后(n²*LLKS)甚至会大于原边侧漏感,这将对开关电源效率产生非常不好的影响。
那我们有什么方法来测量,从而知道变压器的漏感呢?
1. 原边侧漏感测量:将副边绕组短路,再测量原边绕组的开路电感值;副边绕组短路实际上抵消了所有的耦合电感,所以此时测试到的是原边侧漏感;
——胖友们可以思考一下:副边侧绕组短路,即所有通过变压器磁芯的能量都会被副边绕组给释放掉,不会对原边绕组产生任何的阻碍(感抗),所以此时对于变压器原副边耦合部分是短路的,那么剩下能测试到的就是原边侧漏感。
1, 用粗导线将变压器副边管脚直接短路,然后再开路的原边侧绕组两端测量:LLKP。
2. 变压器总漏感测量:总漏感需要考虑实际应用电路和走线影响。
1, 在应用电路板上,用长度尽可能短粗的铜导线直接将输出二极管两端短路;
2, 再将输出电容器两端焊盘位置短路;
3, 最后在开路的原边侧绕组两端测量有效漏感:LLK。
2.2 稳压二极管钳位损耗
我们已经知道了变压器漏感的大小:LLK = LLKP + n²*LLKS,所以在每个开关周期内的漏感能量是:E = (1/2) * LLK * I²pk,式中Ipk是峰值开关电流;但是这并非稳压二极管的钳位损耗,原边侧绕组与漏感串联,所以漏感试图通过稳压二极管的续流来复位,此时原边绕组被迫持续提供串联电流,有一部分能量会进入稳压管钳位电路,直到漏感完全复位,其实际损耗为:Pz = E = (1/2)* LLK *I²pk* [Vz/(Vz-Vor)],所以如果选择稳压管电压Vz接近Vor,那么钳位损耗会迅速上升,因此需要注意Vor的值,即必须仔细选择匝数比。
3. 举个栗子(有需要的可以看下)
输入电压为:90VAC~270VAC;输入功耗:74W;设计输出:5V@10A;开关频率:150KHz。MOS管额定工作电压600V。
3.1 确定VOR与Vz
最大输入电压时变压器上的最大直流电压:Vinmax = 270*√2 = 382V;考虑MOS管的降额(裕量)和最大耐压,Vds要求小于570V;在MOS管关断瞬间的Vds = VIN + Vz = 382V + Vz < 570V,则可得Vz < 188V,选择Vz = 180V。
再考虑Vz在正常工作电压下(VOR)的钳位损耗,根据损耗曲线可发现:Vz/ VOR = 1.4时在消耗曲线上明显下降,选择该值为最优值,所以VOR = Vz/1.4 = 128V。
3.2 匝数比
假设副边输出5V的串联二极管正向压降为0.6V,那么匝数比:n = Vor/(Vo+Vd) = 128V/5.6 =22.86。
3.3 最大占空比
在最大输入电压Vinmax下我们得到了Vz和VOR,还需研究最小输入电压Vinmin下的情况,因为Vinmin是BUCK-BOOST拓扑中电感器设计需考虑的最恶劣情况(电流最大);最小输入直流Vinmin = 90V *√2 = 127V,因此可得到最小输入电压时占空比:D = Vor/(Vor+Vinmin) = 128/(128+127) ≈ 0.5。该值为正常工作情况下的Dmax,因为当输入电源电压下降时,占空比将会增大以保持调整电压。但当出现异常情况时,例如电源Vin掉电时,占空比会进一步增加以维持输出的稳定(除非遇到电流或占空比限制),因此必须保证的调整时间,即掉电阶段的开关周期数量,来选择合适的输入电容器和最大占空比限制(Dlim:一般设置70%)。输入功率电容按照3F/W的经验来估算,预估效率为70%的74W电源所需输入功率为74/0.7 = 106W;所以应该使用:106uF*3 = 318uF(330uF)的输入电容器。
3.4 原副边有效负载电流
5V电源电平,74W功耗,可得到负载电流Io = 74W/5V ≈ 15A,原边绕组输出电压VOR,负载电流为IOR = Io/n = 15/22.86 = 0.656A。
3.5 实际占空比
电源拓扑实际占空比很重要,因为它会导致变压器工作时的峰值电流和响应的磁场显著增加。假设电源效率为70%,可得Pin = Po/0.7 = 74/0.7 = 105.7w;可得平均输入电流Iin = Pin/Vin = 105.7w/127 = 0.832A。
平均输入电流Iin与实际占空比D相关,Iin/D是原边绕组电流斜坡的中心值,即ILR。于是有:Iin/D = IOR/(1-D),D = Iin/(Iin + IOR) = 0.832/(0.832+0.656) = 0.559。
3.6 实际原副边电流斜坡中心值
副边绕组电流斜坡中心值IL = Io/(1-D) = 15/(1-0.559) = 34.01A;
原边绕组电流斜坡中心值ILR = IL/n = 34.01/22.86 = 1.448A。
3.7 峰值开关电流
已知ILR = 1.448A,就能计算出所选电流纹波率下的峰值电流:Ipk = ILR*(1+r/2) = 1.448A*1.25 = 1.86A;由此可以设置控制器的电流限制。
设计离线式变压器时,出于降低高频铜损即减小变压器尺寸的原因,通常将r设置在0.5左右。
3.8 伏秒积
在Vinmin时,有Von = Vin = 127V,则开关导通时间Ton = D/f = 0.559/150K = 3.727us;
可得伏秒积为:Et = Von*Ton = 127*3.727 = 473 V.us。
3.9 原边绕组电感值
按照L*I法则,原边绕组电感值Lp =(1/Ilr)*(Et/r) = 473/(1.448*0.5) = 636uH。
3.10 选择磁芯
在设计磁性元件时,需要加入气隙来改善磁芯的储能能力(具体原理参考:《电感器特性原理》中关于气隙的内容),没有气隙时,磁芯储能很少,而且也容易饱和。但增加气隙后,电感值L会降低,所以对应所需的r值,还需要保证一定的L值。加入气隙越大,则需要绕组匝数越多,这会增加绕组铜损。此外还需要更多的窗口面积来容纳这些绕组(下一节介绍“窗口面积”的概念)。综合考虑这些因素,Ve = 0.7* [(1+r)²/r]*(Pin/f)cm³,所以可得Ve = 0.7*(2.5²/0.5)*[105.7/(150*f)) = 6.17 cm³。
对应EI-30磁芯,根据数据手册Ae = 1.11 cm²,Le = 5.8cm,体积Ve = Ae*Le = 6.438 cm³。
3.11 绕组匝数
根据方程B = L*I/(N*A),在给定频率下,关于r的方程与关于L的方程等效,因此结合这些方程公式,磁通密度变化取最大值,即可得到关于r的电压相关方程:N = (1+r/2)*(Von*D)/(2*Bpk*Ae*f);因此即是没有材料的磁导率,气隙等信息,也可知道磁通密度为B,面积为Ae的磁芯所需要的绕组匝数。对于铁氧体磁芯,磁通密度B不能超过0.3T,所以解关于N(原边绕组Np)的方程可得:
Np = (1+0.5/2)*(127*0.559)/(2*0.3*1.1*150*10³/10⁴) = 35.5砸;下一步还需验证是否适合磁芯的窗口面积,还有是否有合适的:骨架,隔离带,安全胶带,副边绕组和套管等。如果需减小Np匝数,则可采用如下方式:增加r值,减小占空比,或取更高的磁通密度变化值。
然后可得副边绕组匝数Ns = Np/n = 35.5/22.86 = 1.55砸。匝数需要取整,如果取1砸则有较大的漏感,一般取 Ns≈ 2砸,那么Np = 2*22.86 ≈ 46砸。
3.12 实际磁通变化
根据电压方程,解得Bpk = (1+2/r)*(Von*D)/(2*np*Ae*f),我们知道B与np成反比,假如35.5砸对应0.3T的磁通密度,那么46砸的Bpk = 35.5/46 *0.3 = 0.2315T。
磁通密度的摆幅与幅值的关系:∆B = 2*Bac = 2r/(2+r)*Bpk = (1/2.5) *0.2315 = 0.0926T。交流分量Bac是磁通变化量的一半,即0.463T(r = 0.5)。
3.13 气隙
考虑材料的磁导率,L与磁导率的关系方程有:L = (1/z)*[(μ*μ0*Ae)/Le]*N²,其中z为气隙系数:z = (Le+μ*Lg)/Le(具体原理及推理过程参考:《电感器特性原理》)。z可以取不小于1的任何值,假设z =10,则可以提高无气隙磁芯10倍的能量处理量;但增加能量处理量的同时,若想保持L不变,则需增加匝数;一般z选择10~20之间。根据已知条件来计算气隙系数:
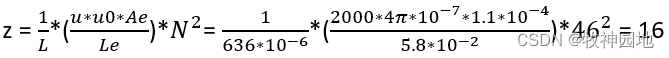
求解气隙的长度:z = (Le+μ*Lg)/Le,16 = (5.8+2000*Lg)/5.8,可得Lg= 0.435mm。