目录
前言
一、FOC简介
1、概述
2、框图详解
二、FOC控制核心—坐标变换
1、CLARKE变换
2、PARK变换&反变换
三、FOC闭环回路
四、SVPWM解析
总结
前言
声明：学习笔记来自正点原子B站教程，根据自己理解进行精简总结，仅供学习交流！！
一、FOC简介
1、概述
FOC（ Field Oriented Control ）直译即磁场定向控制，又称为磁场矢量控制（VC，Vector Control），特点：通过精确地控制磁场大小与方向，使得电机的运动转矩平稳、噪声小、效率高，并且具有高速的动态响应。
之前介绍直流无刷电机时用的时六步换相法（左），磁场每次旋转60°，对于机械臂等领域这样太不精确，所以使用FOC（右），可控制每一相的电流强度实现360°无死角的磁场方向合成。两者具体对比如下：
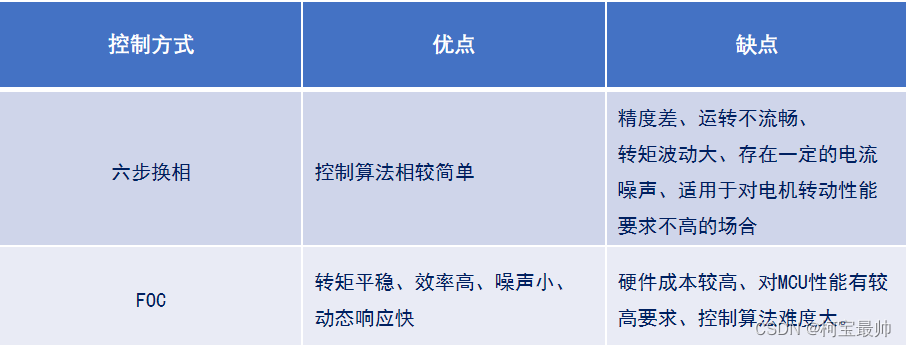
注意：虽然FOC法常用于直流无刷电机中的PMSM永磁同步电机，但BLDC同样可以使用FOC的方式进行控制。
2、框图详解
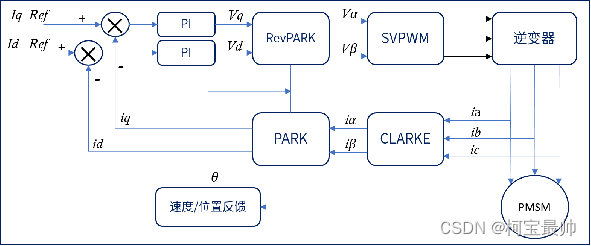
PI即PID控制，只不过这里只用到P和I；逆变器即之前直流无刷电机中的三相逆变电路，通过三个半桥控制电机。
首先对电机三相电流进行采样得到：ia、ib、ic；然后将ia、ib、ic经过clarke变换得到iα、iβ；将iα、iβ经过park变换得到iq、id；计算iq、id和其设定值iq_Ref、id_Ref的误差；将上述误差输入到两个PID（只用到PI）控制器，得到输出的控制电压Vq 、 Vd；将Vq 、 Vd进行反park变换得到Vα、Vβ；将Vα、Vβ合成电压空间矢量，输入SVPWM模块进行调制，输出该时刻三个半桥的开关状态。
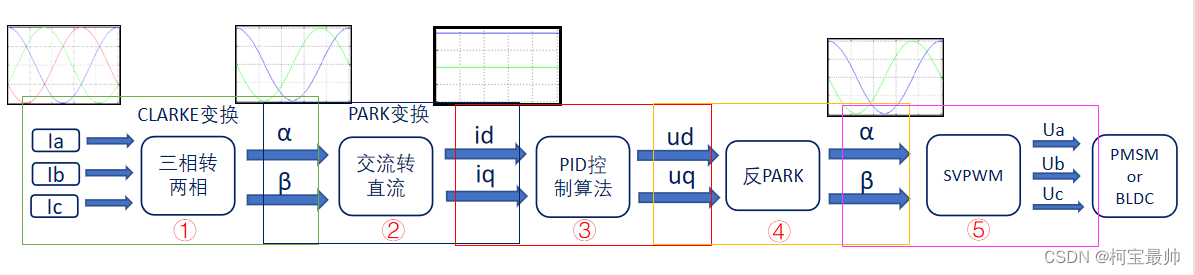
clarke和park变换是为了变为线性好处理分析， 之所以最后还要反变换是因为SVPWM调制算法需要用到α、β。
二、FOC控制核心—坐标变换
坐标变换包含CLARKE变换、PARK变换、反PARK变换。
1、CLARKE变换
三相电路计算困难，将三相等效成二相，变换原则是电流产生的磁场相等（即等效变换）。思路是将三相电流A、B、C投射到直角坐标系转换为两相α、β。三相电流一般只需测出两相就可由KCL得出另一相。
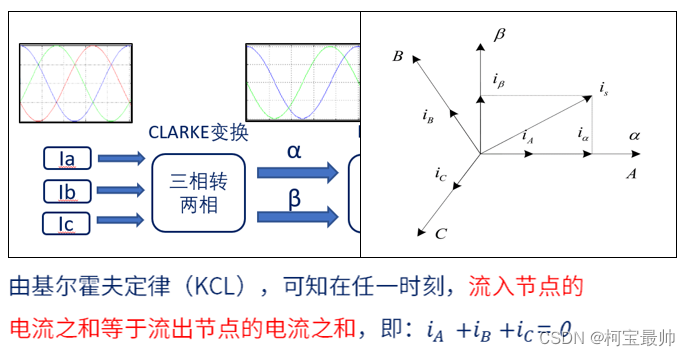
虽然α与β坐标系下少了一维变量，但是新的变量还是非线性的（正弦），只有想办法变换为线性的才利于控制，这就需要park变换。
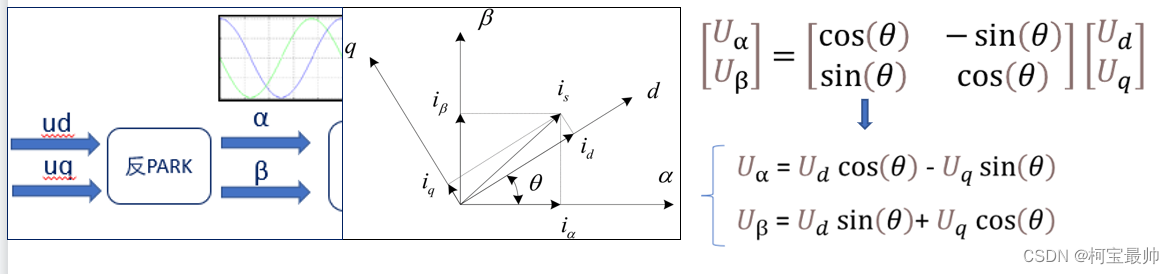
2、PARK变换&反变换
Park变换可以将电机从两相静止坐标系变换到随转子转动的坐标系（dq轴）。d轴方向与转子内磁场方向重合，称为直轴；q轴方向与转子内磁场方向垂直，称为交轴。
其中θ为转子旋转的角度（可通过霍尔/编码器测出）。d - q 坐标系是始终跟着转子旋转的，Id和Iq是恒定不变的两个值，这个坐标系下两个控制量都被线性化了。线性化后要经过PID控制算法，输出后还要进行反PARK变换，因为SVPWM算法的实现需要用到静止的坐标系α,β。
三、FOC闭环回路
电流环：
①通过电流反馈来控制电机电流(扭矩)②控制电机的转速 ③控制电机位置。实际只用到了PI控制，没有引入微分，因为电流的采样率非常高不需要加入微分项。
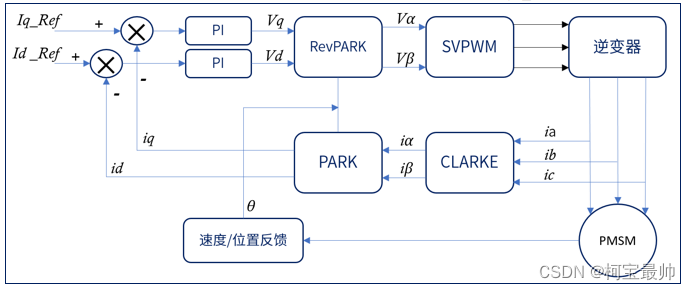
iq是我们需要的（驱动有关），代表了期望的力矩输出。id是我们不需要的（只会增大电流让电机发热），希望尽可能把它控制为0。
速度+电流环：
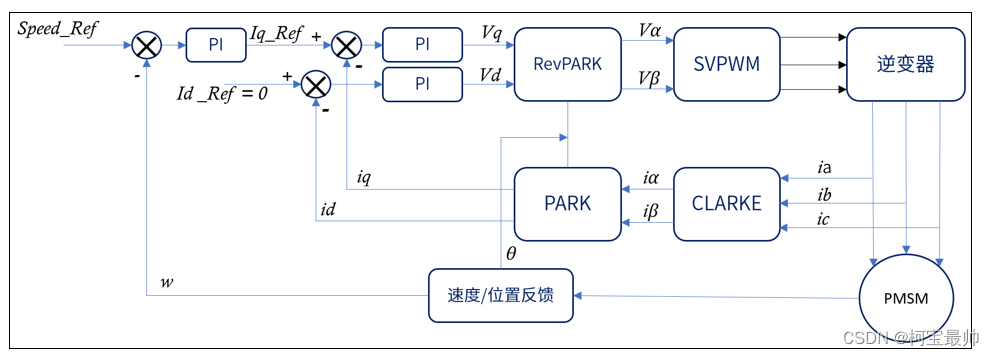
Speed_Ref 是速度设定值，w 是电机转速；将速度环的输出作为电流环的输入，就可以实现速度+电流双闭环控制了。
位置+速度+电流环：
Position_Ref 是位置设定值，Position 是位置反馈。将位置环的输出作为速度环的输入，将速度环的输出作为电流环的输入，就可以实现三闭环控制。
但是位置控制模式的时候，电机的转速会很慢，这时候用平均测速法会存在非常大的误差（转子不动或者动的很慢，编码器就没有输出或者只输出1、2个脉冲）。所以一般使用位置环时，直接使用位置+电流环即可，去掉速度环。
四、SVPWM解析
在介绍SVPWM之前先了解先SPWM！
旋转的PMSM电机波形：
当我们手动将PMSM电机让转子匀速转动时，此时使用示波器观察三相输出电压（反电动势），你会发现有三组正弦波形，且两两之间的相位差为120°
而正弦波正是FOC驱动无刷电机的手段，利用PWM产生的正弦波就是SPWM波。
了解下SPWM：
通过调整占空比使等效电流近似为正弦波，这种PWM也就是SPWM。SPWM不依赖开关顺序，3相独立调制，类似开环控制，是没有反馈的，只管生成正弦波。
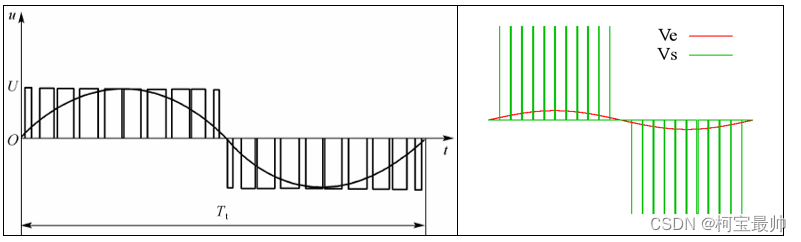
但是SPWM调试方式在FOC实现中并不常用，原因是SPWM要比后面要说的SVPWM的母线电压利用率要低15%。从控制的角度来看，我们根本就不想跟什么三个正弦波打交道，所以就用到了坐标变换。
SVPWM解析
SVPWM （Space Vector Pulse Width Modulation）即：空间电压矢量。由三相逆变器的六个开关元件（MOS管）组成的特定开关模式，使输出电压波形尽可能接近于理想的正弦波形。着眼于如何使电机获得理想圆形磁链轨迹。
SVPWM算法的目的，就是使用逆变电路的6个开关状态把在空间中旋转的矢量表示出来，我们把这个矢量称为空间电压矢量。SVPWM算法实际上计算的是三相逆变器的六个开关何时导通，何时切断（同一列不可同时导通或关闭，即同一半桥不可同时导通，所以有2x2x2=8种情况）
举例分析：
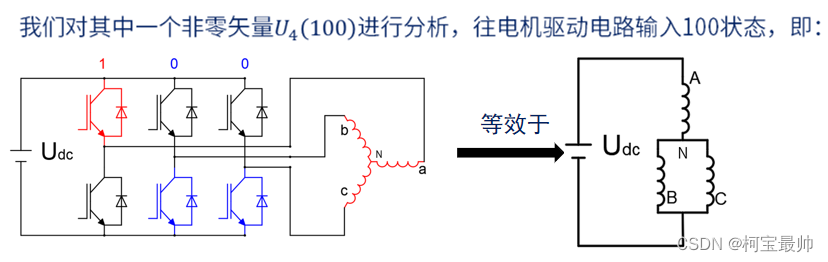
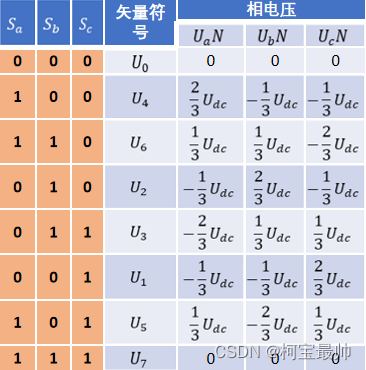
根据三相电阻相等，即Ra=Rb=Rc，再根据串联分压定理：
则同理可得8种情况的相电压如上右图表格（非零矢量的幅值相同，都是2/3Udc）
坐标系表示空间矢量:
以U4(100)合成的空间电压矢量为例(以指向中心点O的方向为负，反之为正，如A相OA正，AO负)，即：
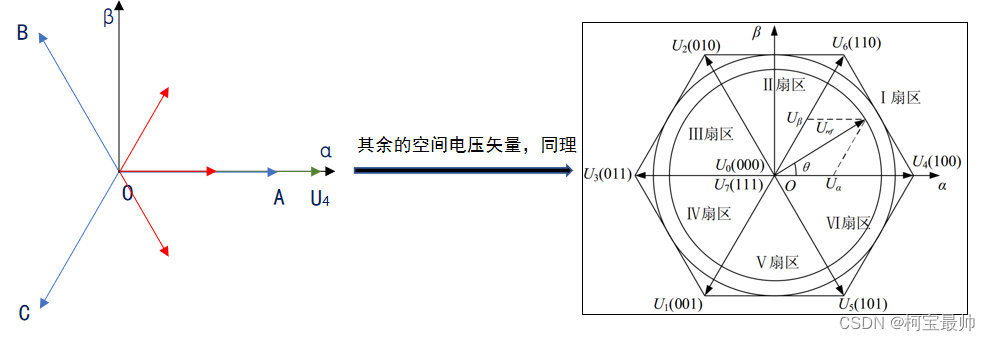
但是这8种开关组合只能合成6个方向的空间电压矢量，如何合成任意位置空间电压矢量？
在一个扇区内，相邻两个电压矢量以及零矢量，按伏秒平衡的原则来合成该扇区内的任意电压矢量 ，即：（本质思路是控制电压时间占比）
只要合理地配置相邻的两个基向量和零矢量在一个周期中的占比，就可以合成出等效的任意空间电压矢量了
但是还有两个问题，如何计算相邻电压矢量与零矢量在一个周期内的时间占比？期望的电压矢量所属扇区判定？
时间占比计算:
假设在扇区一，那么此时等式为：
结果最后为什么除以2平均分配给零矢量T7和T0呢？（以7段式（7periods）为例）
每个状态切换的时候，都只有一个相发生了转变，从而降低MOS管的开关损耗；合理插入两个零矢量，并且对零矢量在时间上进行了平均分配，以使产生的PWM对称，从而有效地降低了PWM的谐波分量。
扇区判定：
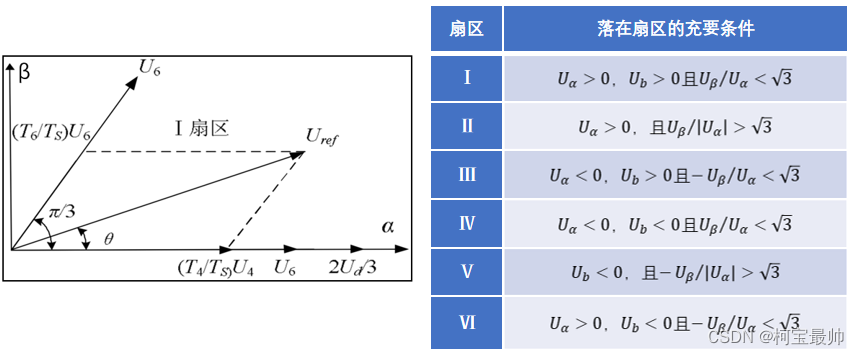
总结
遇到挫折，要有勇往直前的信念，马上行动，坚持到底，决不放弃，成功者决不放弃，放弃者绝不会成功。成功的道路上，肯定会有失败；对于失败，我们要正确地看待和对待，不怕失败者，则必成功；怕失败者，则一无是处，会更失败。
今天的学习分享到此就结束了，我们下次再见！！
往期精彩：
控制理论 PID算法
STM32定时器输入捕获（IC）
STM32定时器输出比较（PWM波）
STM32定时中断
STM32外部中断
STM32GPIO精讲
…
