来源：力扣（LeetCode）

描述：

给定正整数 k ，你需要找出可以被 k 整除的、仅包含数字 1 的最 小 正整数 n 的长度。

返回 n 的长度。如果不存在这样的 n ，就返回 -1。

注意： n 不符合 64 位带符号整数。

示例 1：

输入：k = 1
输出：1
解释：最小的答案是 n = 1，其长度为 1。

示例 2：

输入：k = 2
输出：-1
解释：不存在可被 2 整除的正整数 n 。

示例 3：

输入：k = 3
输出：3
解释：最小的答案是 n = 111，其长度为 3。
 

提示：

• 1 <= k <= 10⁵

方法：遍历

思路与算法

题目要求出长度最小的仅包含的 1 的并且被 k 整除的正整数。我们从 n = 1 开始枚举，此时对 k 取余得余数 resid = 1 mod k。如果 resid 不为 0，则表示 n 当前还不能被 k 整除，我们需要增加 n 的长度。令 n_new = n_old ×10 + 1，resid_new = n_new mod k 。将 n_old 代入其中可得：

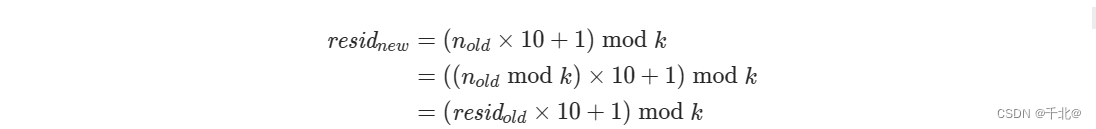
从上式可以发现，新的余数 resid_new 可以由 resid_old 推导得到。因此在遍历过程中不需要记录 n，只需记录 resid。由于 resid 是对 k 取余之后的余数，因此种类数不会超过 k。

在遍历过程中如果出现重复的 resid，表示遇到了一个循环，接着遍历下去会重复循环中的每一步，不会产生新的余数。所以我们用一个哈希表记录出现过的余数，当更新 resid 后发现该值已经在哈希表时，直接返回 −1。否则我们一直遍历，直到 resid 变为 0。最终哈希表中的元素个数或者遍历次数就是实际 n 的长度。

代码：

class Solution {
public:
    int smallestRepunitDivByK(int k) {
        int resid = 1 % k, len = 1; // resid为余数，len为数字长度，初始值为1
        unordered_set<int> st; // 创建一个无序集合，用于存储余数
        st.insert(resid); // 插入余数1
        while (resid != 0) { // 当余数为0时退出循环
            resid = (resid * 10 + 1) % k; // 计算下一个余数
            len++; // 数字长度+1
            if (st.find(resid) != st.end()) { // 如果余数重复出现，则无解
                return -1;
            }
            st.insert(resid); // 将余数插入集合
        }
        return len; // 返回数字长度
    }
};

优化

注意到当 k 为 2 或者 5 的倍数时，能够被 k 整除的数字末尾一定不为 1，所以此时一定无解。

那当 k 不为 2 或者 5 的倍数时一定有解吗？我们做进一步的分析。

resid 随着 1 的增加，最后一定进入循环，我们能找到两个对 k 同余的 n 和 m。假设 n > m，那么一定有以下等式成立：

(n − m) ≡ 0 (mod k)
n − m 可以表示为 11…100…0 的形式，因此有 11 … 100 … 0 ≡ 0(mod k)。

如果此时 k 不为 2 或 5 的倍数，则 k 与 10 没有公因数，k 与 10 互质。n − m 末尾的 0 可以除掉，因此 11…1 ≡ 0(mod k)，问题一定有解。

代码：

class Solution {
public:
    int smallestRepunitDivByK(int k) {
        // 若 k 能被 2 或 5 整除，则无解，返回 -1
        if (k % 2 == 0 || k % 5 == 0) {
            return -1;
        }
        // 初始化余数为 1，表示一个数的最低位是 1
        int resid = 1 % k, len = 1;
        // 若余数不为 0，继续迭代
        while (resid != 0) {
            // 计算下一个数的余数，下一个数在当前余数后加一个 1
            resid = (resid * 10 + 1) % k;
            len++;
        }
        // 返回数字 1 的最小重复次数
        return len;
    }
};

执行用时：0 ms, 在所有 C++ 提交中击败了100.00%的用户
内存消耗：5.7 MB, 在所有 C++ 提交中击败了93.94%的用户
复杂度分析
时间复杂度：O(k)。过程中最多会遍历 k 次。
空间复杂度：O(1)。如果使用哈希表，空间复杂度为 O(k)。
author：LeetCode-Solution