一、题目描述

原题连接： 234. 回文链表
题目描述：
给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true ；否则，返回 false 。

示例 1：

输入： head = [1,2,2,1]
输出： true

示例 2：

输入： head = [1,2]
输出： false

提示：
链表中节点数目在范围[1, 105] 内
0 <= Node.val <= 9

进阶：你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题？

二、解题

1、方法1——复制值到数组后用双指针

1.1、思路分析

一个最容易想到的方法就是先将链表个节点的值赋值到一个等长的数组中，然后再在数组上使用双指针来判断数组是否回文：
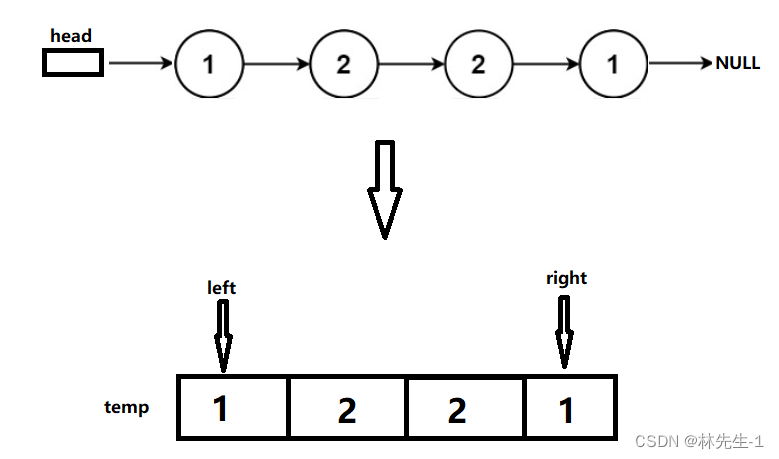
在这里插入图片描述

1.2、代码实现

有了以上思路，那我们写起代码来也就水到渠成了：

bool isPalindrome(struct ListNode* head) {
    struct ListNode* cur = head;

    // 先算出链表的长度
    int len = 0;
    while (cur) {
        len++;
        cur = cur->next;
    }

    // 创建数组
    int* temp = (int*)malloc(len * sizeof(int));
    if (NULL == temp) {
        perror("malloc fail");
        exit(-1);
    }

    // 将链表的值复制到数组
    cur = head;
    int i = 0;
    while (cur) {
        temp[i] = cur->val;
        cur = cur->next;
        i++;
    }

    // 使用双指针判断
    int left = 0;
    int right = len - 1;
    while (left < right) {
        if (temp[left] != temp[right]) {
            free(temp);
            temp = NULL;
            return false;
        }
        left++;
        right--;
    }
    free(temp);
    temp = NULL;
    return true;
}

时间复杂度：O(n)，n为链表的长度。
空间复杂度：O(n)，我们需要额外的n个空间来存储链表节点的值，故空间复杂度为O(n)。

2、方法2——反转另一半链表

2.1、思路分析

因为是单链表，所以我们不能从后往前遍历，但我们可以把链表反转之后再从前往后遍历，这也等同于从后万千遍历。
所以我们可以先将后半部分的链表反转过来之后，再将它与前半部分的链表同步遍历进行比较：
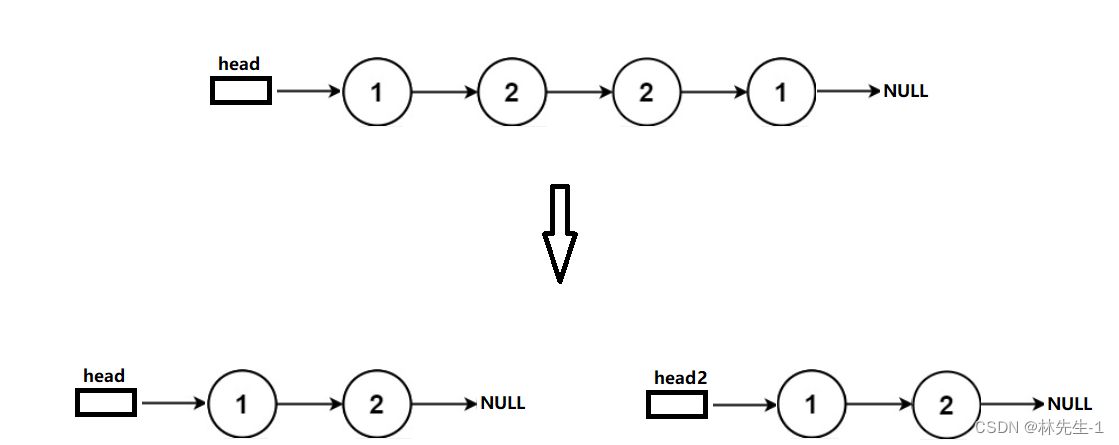
在这里插入图片描述
而为了反转后一半链表我们得先找到链表的中间节点，我们可以沿用[LeetCode 876. 链表的中间结点]中经典的快慢指针方法。
而反转操作我们就可以沿用[LeetCode 206. 反转链表]的头插法。
最后我们使用两个指针同步遍历两个链表：
在这里插入图片描述
只要遇到一个cur1->val != cur2->val的情况就可以返回false，当其中一个指针为空时就可以停止，并返回true。

2.2、代码实现

有了以上思路，那我们写起代码来也就水到渠成了：

// 先写一个函数，返回链表的中间节点
struct ListNode *FindMid(struct ListNode *head) {
    if (NULL == head) {
        return NULL;
    }
    struct ListNode *fast = head; // 快指针，一次走两步
    struct ListNode *slow = head; // 慢指针，一次走一步
    while (fast && fast->next) {
        fast = fast->next->next;
        slow = slow->next;
    }
    return slow;
}

// 再写一个函数，将一个链表翻转
struct ListNode *ReverseList(struct ListNode *head) {
    if (NULL == head) {
        return NULL;
    }
    struct ListNode *newhead = NULL;
    struct ListNode *cur = head;
    struct ListNode *pre = NULL; // cur的前一个节点
    while (cur) {
        pre = cur;
        cur = cur->next;

        // 头插
        pre->next = newhead;
        newhead = pre;
    }
    return newhead;
}
bool isPalindrome(struct ListNode* head){
    struct ListNode *head1 = head;
    struct ListNode *mid = FindMid(head);
    struct ListNode *head2 = ReverseList(mid);
    struct ListNode *cur1 = head1;
    struct ListNode *cur2 = head2;
    while (cur1 && cur2) {
        if (cur1->val != cur2->val) {
            return false;
        }
        cur1 = cur1->next;
        cur2 = cur2->next;
    }
    return true;
}

时间复杂度：O(n)，n为链表的长度。
空间复杂度：O(1)，我们只需要用到常数级的额外空间。

2.3、补充

可能有人看到代码后会异或，我的代码里并没有向上面图解中的那样把前半部分的链表的尾的next个置空啊：
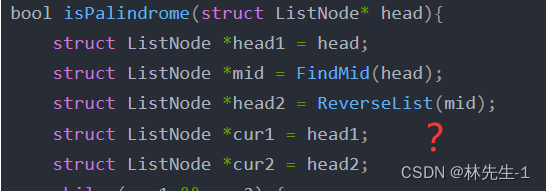
在这里插入图片描述

其实这一步是可有可无的，而我们必须要做的是将后半部分反转后的链表的尾节点的next置空。因为如果原链表的节点数是偶数，后半部分的链表的节点是也是偶数，也就是后半部分的节点数是原链表节点数的一半，所以即使我们没有吧前半部分的尾给置空，那时也是cur2先为空：
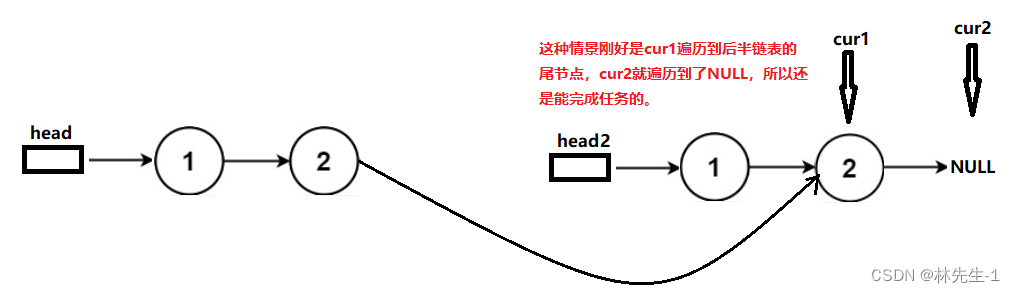
在这里插入图片描述
而当原链表的节点数为奇数时，后半部分的链表就会比前半部分多出一个节点：

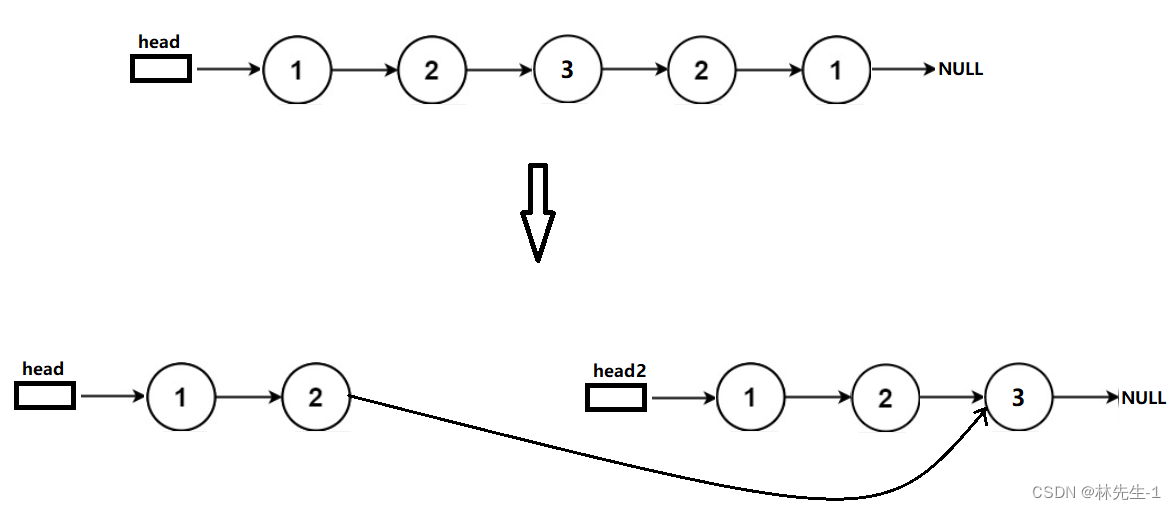
但我们发现cur1和cur2会同时到达反转部分的最后一个节点，最后也同时为空：

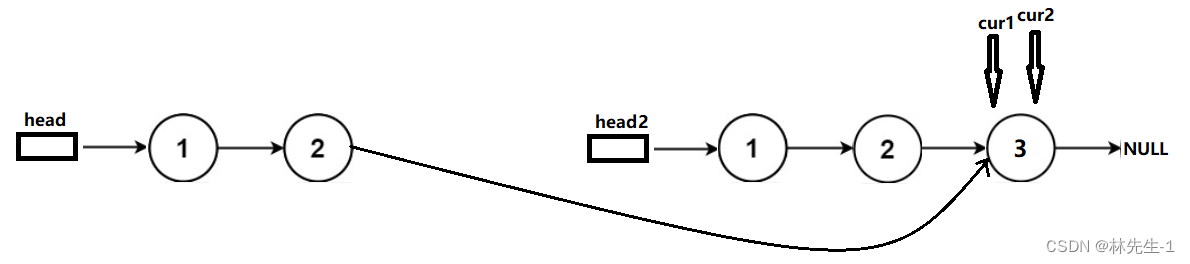
所以说，将前半部分的尾置空的操作是可有可无的。

3、方法3——递归

3.1、思路分析

递归的思路其实类似于双指针，先让递归一层层深入，直到走到链表的尾，在通过一层层的返回来模拟指针从后往前走的动作。
我们需要额外创建一个全局的指针，在每次递归中，如果本次递归满足前面的节点的val和后面的节点的val相同，就让前面的节点往后走一步。如果不相同就直接返回false。

3.2、代码实现

有了以上思路，那我们写起代码来也就水到渠成了：

// 定义一个全局的节点指针
 struct ListNode *leftNode;
 // 先写一个递归函数
 bool recursivelyCheck(struct ListNode *rightNode) {
     if (rightNode) {
         if (!recursivelyCheck(rightNode->next)) {
             return false;
         }
         if (leftNode->val != rightNode->val) {
             return false;
         }
        leftNode = leftNode->next;
     }
     return true;
 }

bool isPalindrome(struct ListNode* head) {
    leftNode = head;
    return recursivelyCheck(head);

}