华中科技大学《计算机图形学》课程

MOOC地址：计算机图形学（HUST）

计算机图形学 | 裁剪与屏幕映射

8.1 裁剪思想

裁剪的概念

观察空间不同，裁剪和屏幕映射的方法不同。

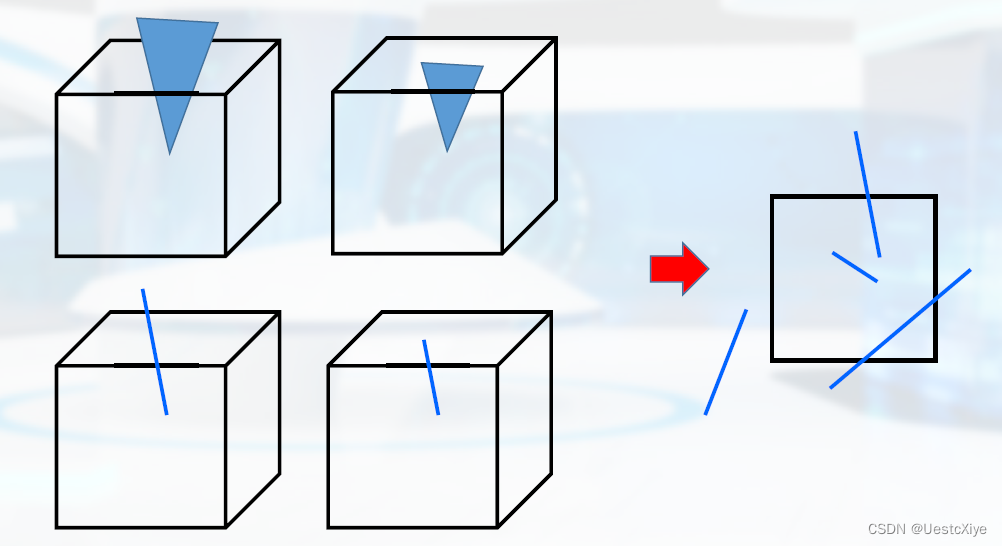
先在二维空间简化要解决的问题：对直线段p₁(x₁,y₁)p₂(x₂,y₂)进行裁剪。

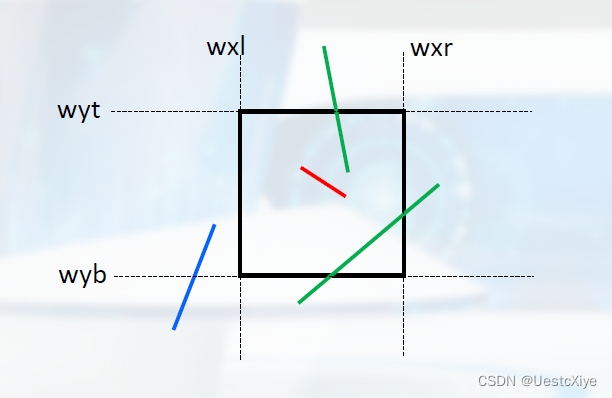
裁剪一条直线段：

1. 判断是否完全落在裁剪窗口内。
2. 如果没有，再判断是否完全落在裁剪窗口外。
3. 既不能确定完全落在裁剪窗口内又不能确定完全落在裁剪窗口外，则计算它与一个或多个裁剪边界的交点。

编码裁剪法

Cohen-Sutherland方法：基于编码的裁剪方法，是最早的最流行的二维裁剪方法。

基本思想：对每条直线段p₁(x₁,y₁)p₂(x₂,y₂)分三种情况处理：

1. 直线段完全可见，“简取”之。
2. 直线段完全不可见，“简弃”之。
3. 直线段既不满足“简取”的条件，也不满足“简弃”的条件，需要对直线段按交点进行分段，分段后重复上述处理。

编码：对于任一端点(x,y)，根据其坐标所在的区域，赋予一个4位的二进制码D₃D₂D₁D₀。

编码规则如下：

• 若x<wxl，则D₀=1，否则D₀=0；
• 若x>wxr，则D₁=1，否则D₁=0；
• 若y<wyb，则D₂=1，否则D₂=0；
• 若y>wyt，则D₃=1，否则D₃=0。

裁剪一条线段时，先求出端点p₁和p₂的编码code1和code2，然后：

1. 若code1 | code2 = 0，对直线段应简取之。
2. 若code1 & code2 ≠ 0，对直线段可简弃之。
3. 若上述两条件均不成立。则需求出直线段不窗口边界的交点。在交点处把线段一分为二，其中必有一段完全在窗口外，可以弃之。再对另一段重复进行上述处理，直到该线段完全被舍弃或者找到位于窗口内的一段线段为止。

具体做法：按左、下、右、上的顺序求出直线段与窗口边界的交点，分段处理。

中点裁剪法

仍然基于Cohen-Sutherland中的区域编码。

基本思想：当对直线段不能简取也不能简弃时，简单地把线段等分为二段，对两段重复上述测试处理，直至每条线段完全在窗口内或完全在窗口外。

具体过程：

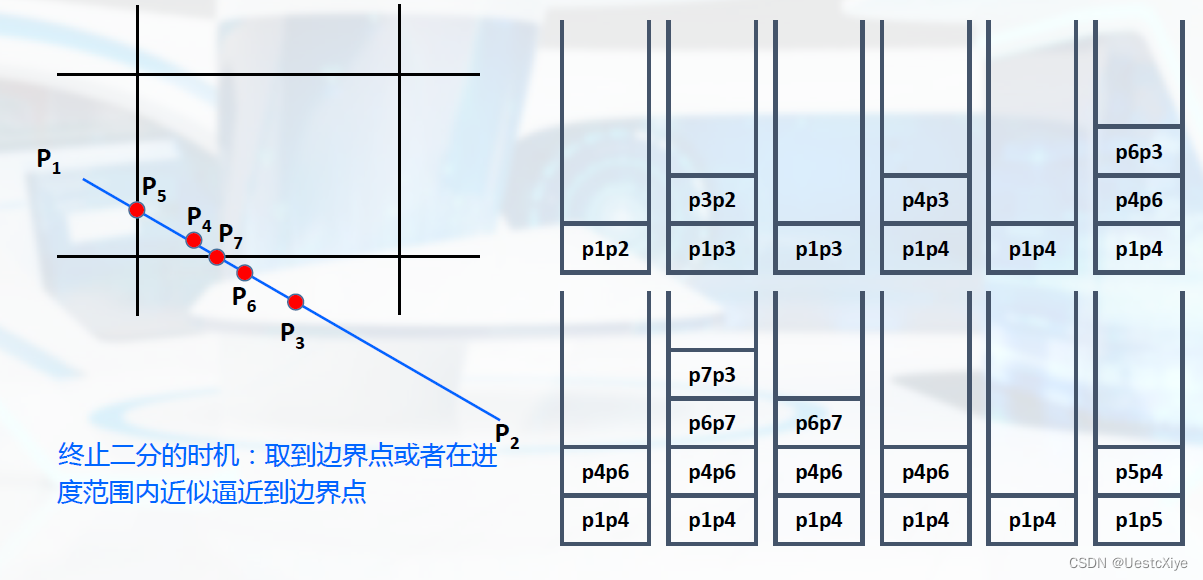
本质：用二分逼近的方法求线段不窗口边界的交点。

Liang-Barsky算法

将线段看成有方向性：外到内、内到外。

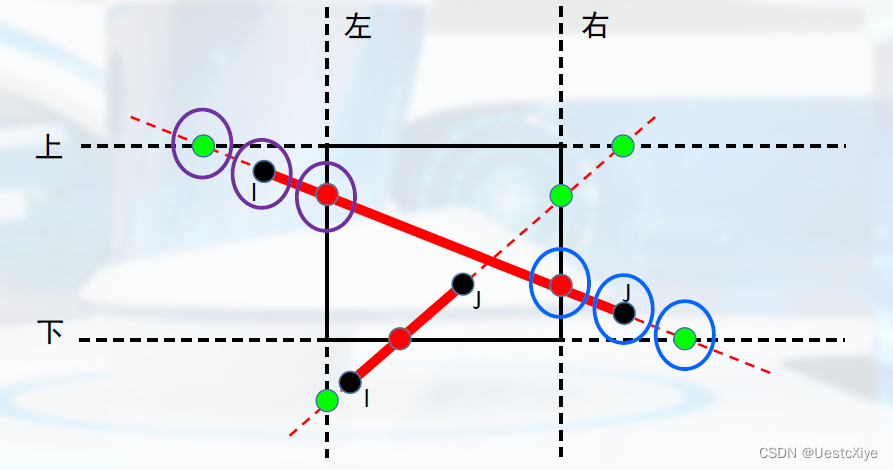
Liang-Barsky裁剪的思想：

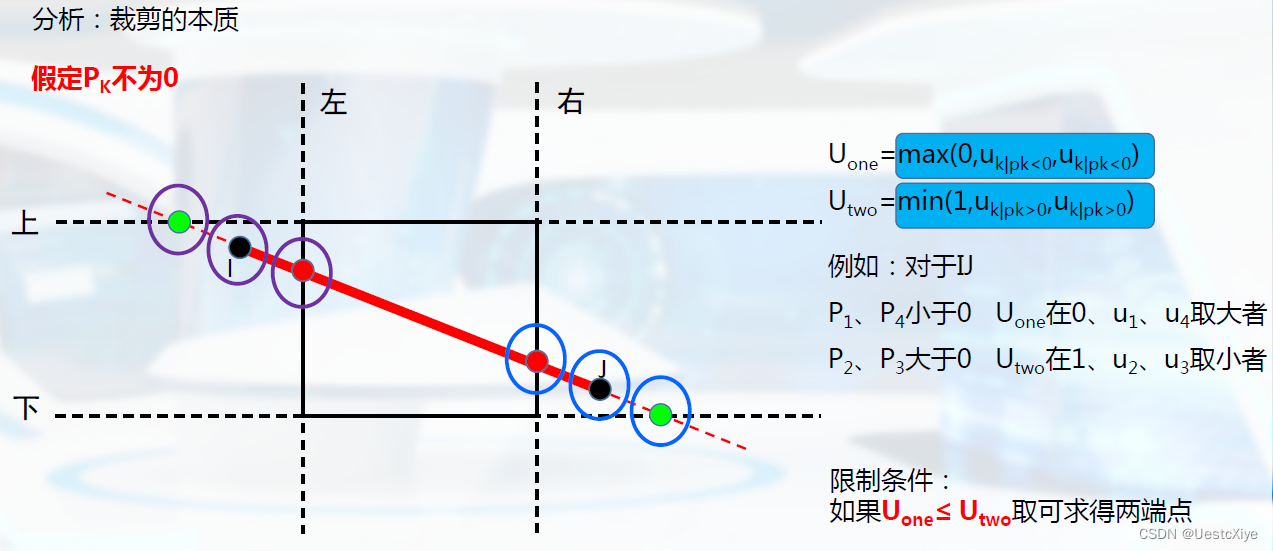
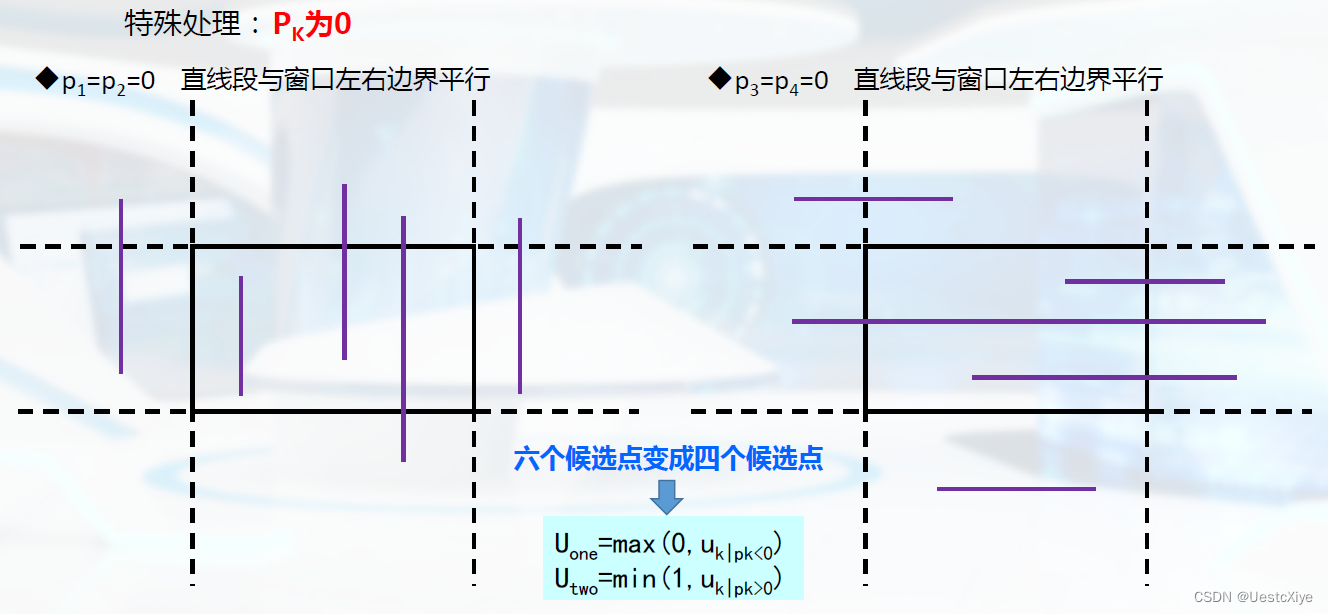
实例：试用liang-barsky算法裁剪图中的线段AB。

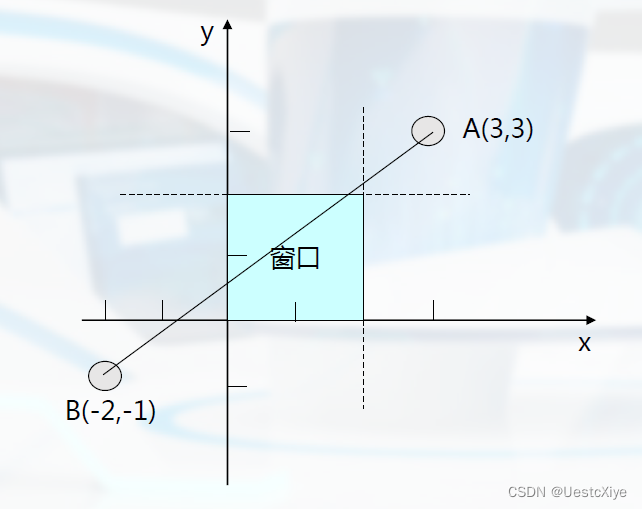
解：直线段AB的参数方程为：

x=3+u·(-2-3)，y=3+u·(-1-3，（0 ≤ u ≤ 1）

即：

x=3-5u，y=3-4u，（0 ≤ u ≤ 1）

这里：wxl=0，wxr=2，wyb=0，wyt=2。

因此：

p1= x1-x2=5>0，q1= x1–wxl=3
p2= x2-x1 =-5<0，q2= wxr –x1=-1
p3= y1-y2 =4>0，q3= y1–wyb=3
p4= y2-y1 =-4<0，q4= wyt –y1=-1

可见P均不为0。

直线段不窗口边界的交点计算如下：
uk·pk=qk，k=1,2,3,4

则u1=0.6, u2=0.2, u3=0.75, u4=0.25。

由于有：p1 、p3大于0，p2、p4小于0

Uone=max(0,uk|pk<0,uk|pk<0)
Utwo=min(1,uk|pk>0,uk|pk>0)

因此：

Uone=max(0,u2,u4)=max(0,0.2,0.25)=0.25
Utwo=min(1, u1,u3)=min(1,0.6,0.75)=0.6

可见Uone<Utwo ,它们分别对应输出直线段的起点和终点。

由于有：x=3-5u，y=3-4u

因此：

Uone对应的交点为I（1.75,2）
Utwo对应的交点为J(0,0.6)
裁剪后输出线段的端点即为I（1.75,2）和J(0,0.6)，四舍五入后为I（2,2）和J(0,1)。

8.2 真正的裁剪——在三维空间遇见多边形

真正的裁剪

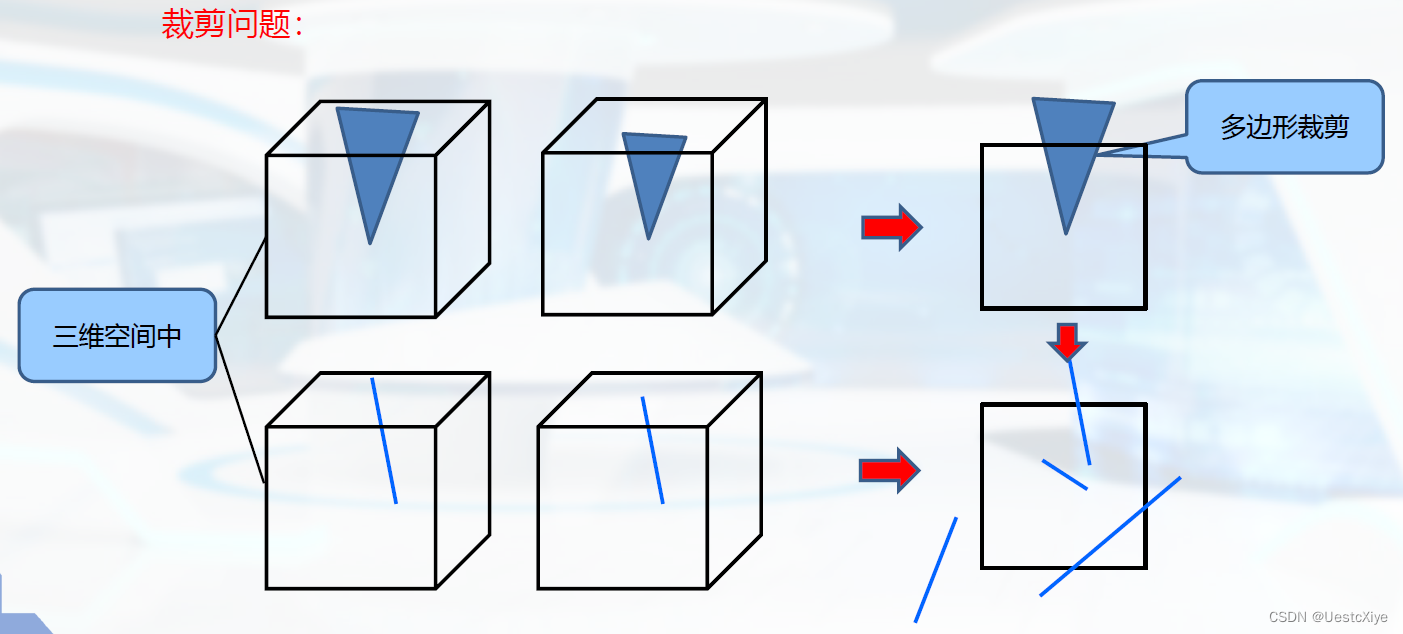
多边形的裁剪

裁剪算法：Sutherland-Hodgeman多边形裁剪

基本思想：将多边形边界作为一个整体，每次用窗口的一个边界对要裁剪的多边形进行裁剪。

顺序：左、下、右、上。

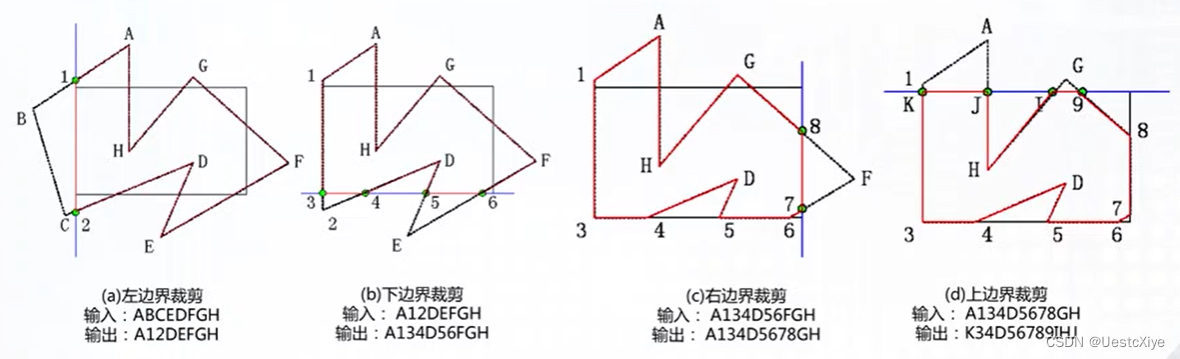
概念：

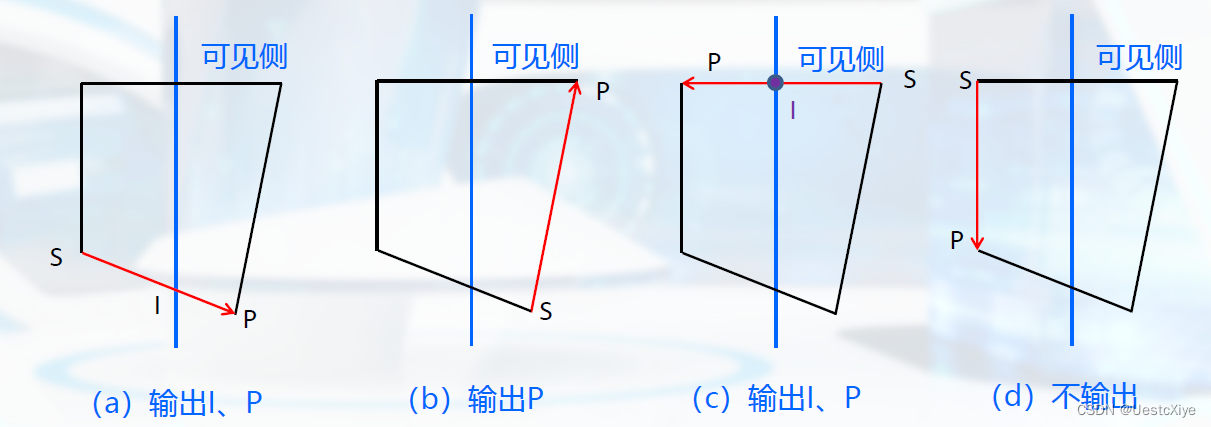
逐边裁剪时遇到的四种情况：

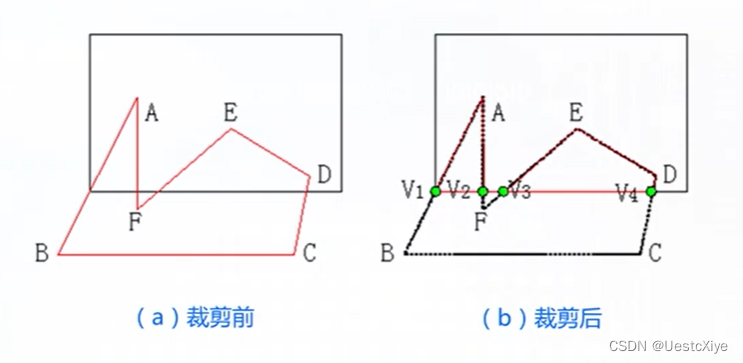
Sutherland-Hodgeman算法的问题：无法正常操作凹多边形。

例如：下面的v2和v3是错误的裁剪点。

解决方案：

• 方案1：将凹多边形分割成两个或更多的凸多边形，然后分别处理各个凸多边形。
• 方案2：修改Sutherland-Hodgeman算法，沿着任何一个裁剪窗口边界检查顶点表，正确地连接顶点对。
• 方案3：采用其他多边形裁剪方法，如Weiler-Atherton算法。

Weiler-Atherton算法

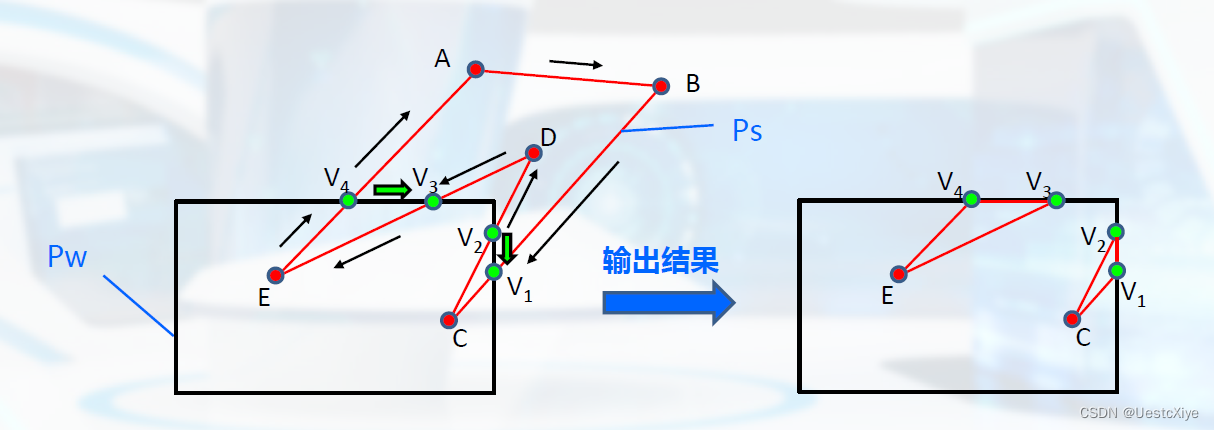
假定按顺时针方向处理顶点，且将多边形定义为Ps，窗口矩形为Pw。

算法从Ps的任一点出发，跟踪检测Ps的每一条边。

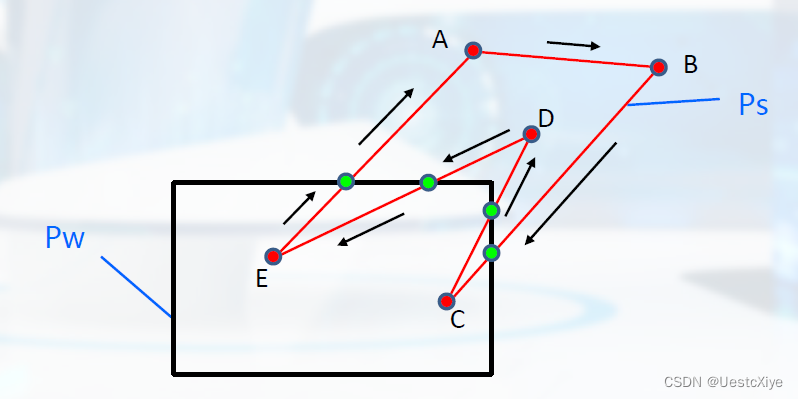
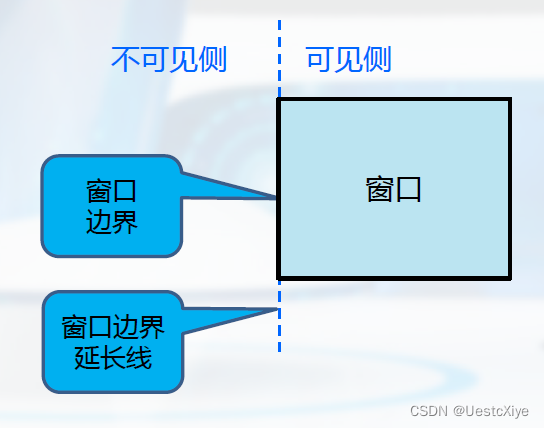
Weiler-Atherton算法步骤：

1. 由不可见侧进入可见侧，则输出可见直线段，转3
2. 由可见侧进入不可见侧，则从当前交点开始，沿窗口边界顺时针检测Pw的边，找到Ps与Pw最靠近当前交点的另一交点，输出可见直线段和由当前交点到另一交点之间窗口边界上的线段，然后返回处理的当前交点
3. 沿着Ps处理各条边，直到处理完Ps的每一条边，回到起点为止

示例：

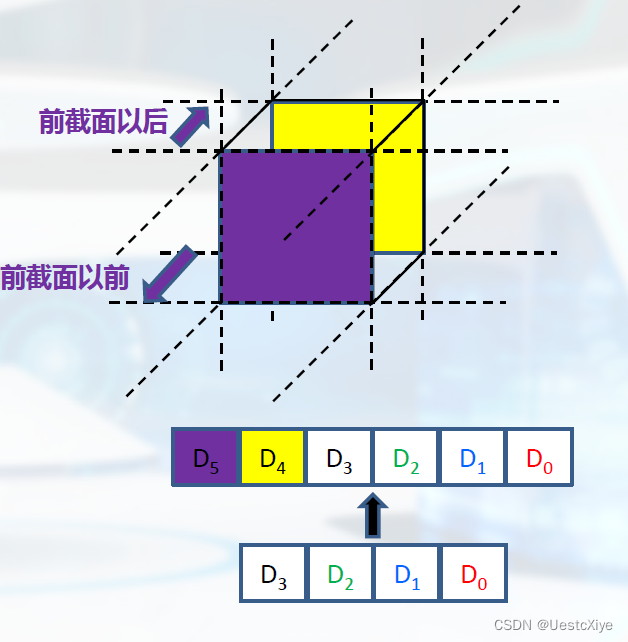
三维空间中的裁剪

Cohen-Sutherland裁剪的推广。

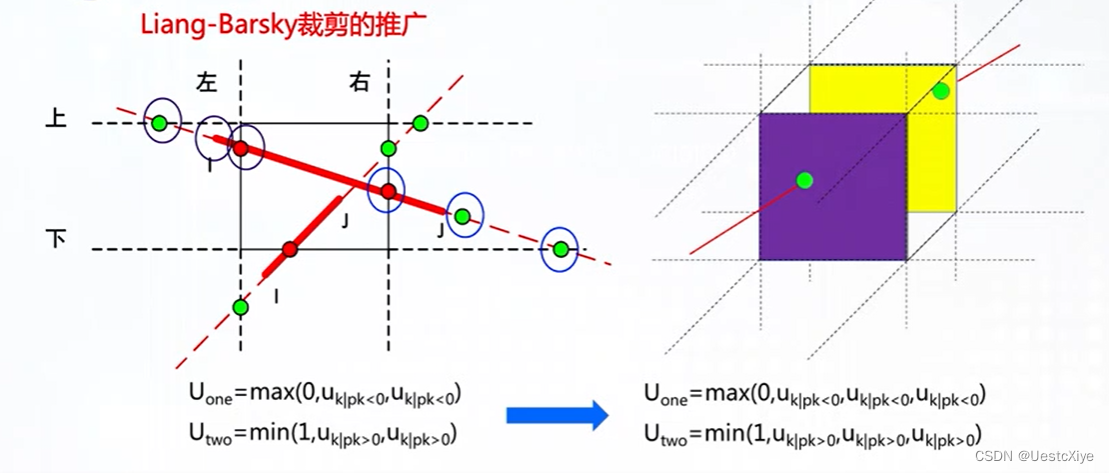
三维形体裁剪问题：Sutherland-Hodgeman算法的推广。

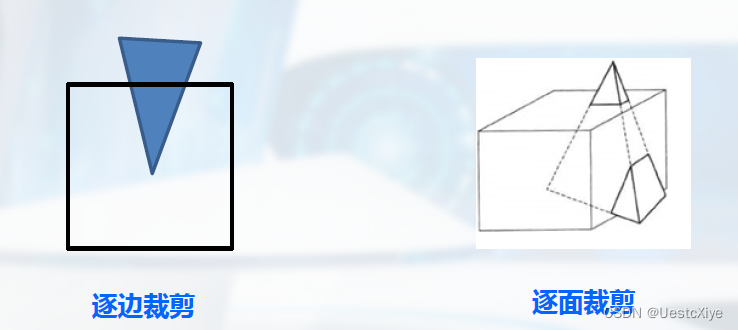
逐边裁剪多边形：逐边裁剪多边形的每条边
输出：顶点序列构成多边形

逐面逐个裁剪多个多边形：逐面裁剪多边形的每条边
输出：顶点序列，构成多面体

8.3 几何阶段的完结：屏幕映射

屏幕映射

屏幕映射：裁剪空间向屏幕空间的映射。

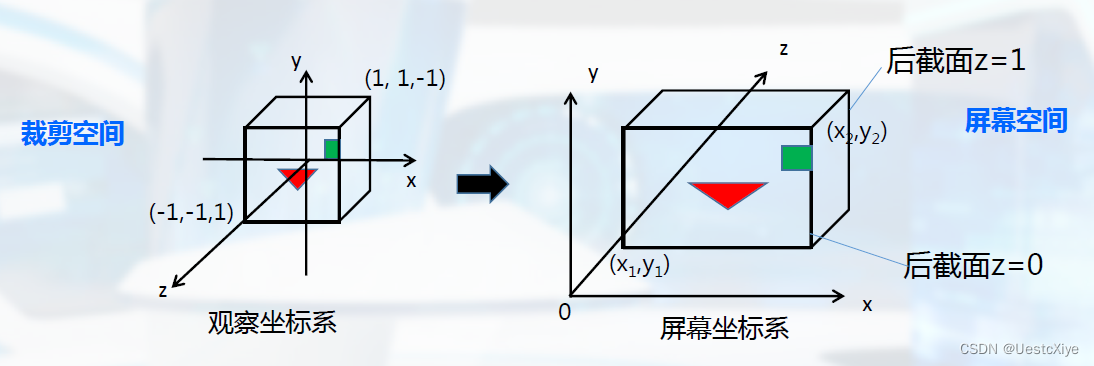
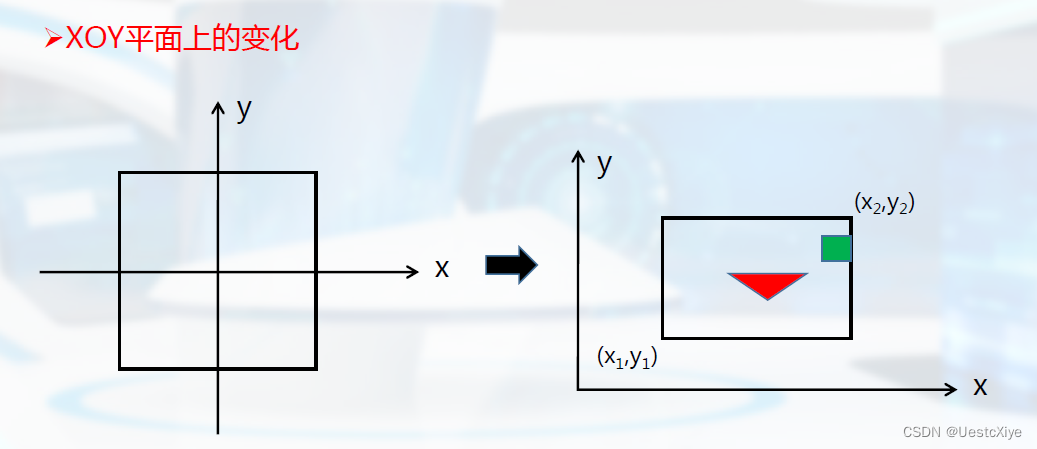
过程分析：

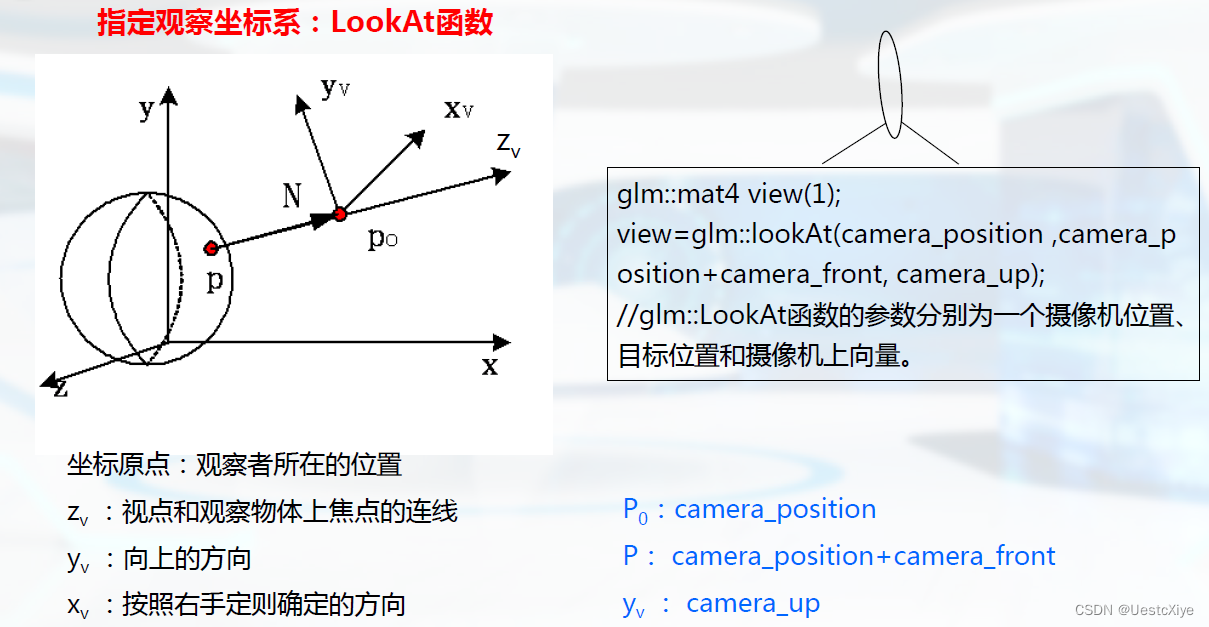
OpenGL的几何阶段实现

指定裁剪空间：以透视投影为例

glm::mat4 proj =glm::perspective(45.0f, 1.3f, 0.1f, 100.0f);

在观察空间中指定裁剪空间：

• 第一个参数定义了视野的角度fov
  对于一个真实的观察效果，它的值经常设置为45.0，但想要看到更多结果你可以设置一个更大的值。
• 第二个参数设置了宽高比，由视口的高除以宽
• 第三个参数设置了前截面的位置
• 第四个参数设置了后截面的位置

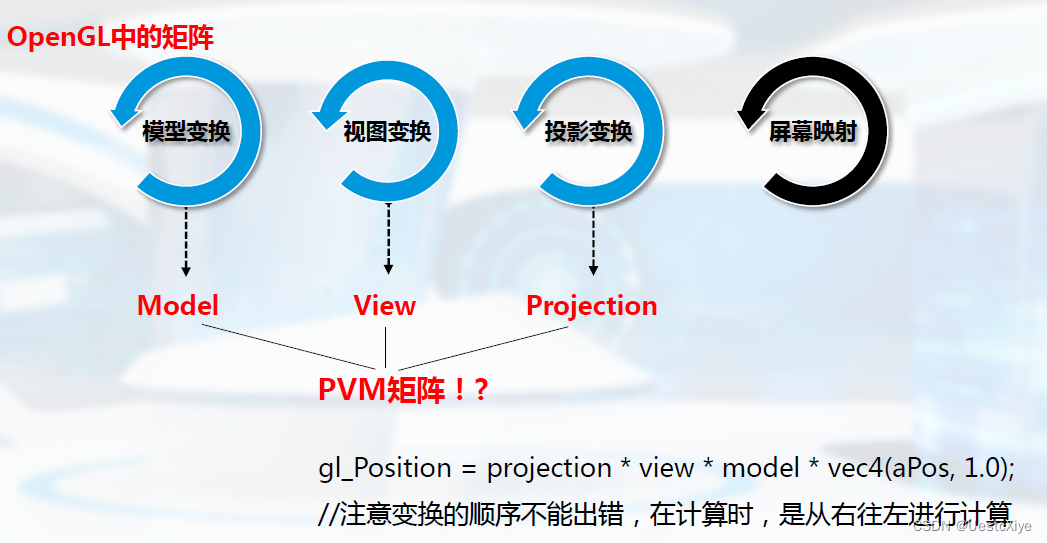
之前的变换基于行矩阵：

现在在OpenGL中改为列矩阵：

OpenGL中的PVM观察变换：

gl_Position = projection * view * model * vec4(aPos, 1.0);