缺失值处理

数据缺失是指数据集中某行记录或某列特征的变量值存在空值的情况。常用的缺失值处理方法主要包括以下几种：

删除法

若数据集中某行记录或某一列特征的数据缺失比率大于指定阈值时，可以认为该行数据或该列特征为无效数据或无效特征，直接删除含缺失数据的记录即可

填充法

基于统计学变量填充

根据特征的类型和分布情况决定采用哪种统计学变量进行填充。

例如：特征是离散型的，可以直接通过众数对缺失值进行填充；特征是连续数值型并且数据分布比较均匀，可以采用平均数对缺失值进行填充，用全局变量或是属性的平均值来代替所有缺失数据；特征是连续数值型但分布倾斜，可以采用中位数进行填充等。

基于插值填充

通过随机插值、拉格朗日插值、多项式插值等方法对缺失的变量值进行填充。

例如：多项式插值法是通过构建多项式来拟合现有的数据，使得所有的样本数据都符合该多项式的分布，需要获取某个样本的缺失值时，通过求解该多项式来获得。

基于模型填充

利用有监督的模型或者无监督的模型来实现缺失值的填充。

例如：K近邻填充是利用聚类的方式来获得某个缺失样本邻近的若干个样本点，通过对这些样本点计算均值或加权平均来进行缺失值填充。

基于预测填充

用预测模型来预测每一个缺失数据。用已有数据作为训练样本来建立预测模型，预测缺失数据。

不处理

使用特殊标记标明缺失值，在后续处理中对其不做处理或者做其他特殊操作

异常值处理

当数据中的某个数据点明显偏离于其他数据点的分布或者某个数据点明显区别于其他的数据点时，将其判定为异常值，对异常值可采用异常数据检测的方法，检测异常值并将其进行去除。

基于统计分析的方法

通过特征的描述信息以及特征值范围来判断数据是否异常。

例如，对于年龄特征，规约其值的范围是[0，200]，当出现了负数或者大于200的数，则判断为异常数据。

基于聚类的方法

一般正常的数据点呈现聚合形态，正常数据出现在密集的邻域周围，而异常点偏离较远，以此来对数据进行判定异常。

基于树的方法

通过划分来判定异常。
例如，孤立森林被认为是最有效的异常检测方法之一，该方法是通过计算样本点的异常关联度分数来进行异常判定，若某样本得到的异常关联度分数较高，且大于阅值时可以判定其为异常。

基于预测的方法

对时序数据根据其预测出来的时序曲线和真实的数据相比，来判定异常值的出现。

数据重采样

针对时序数据可采用数据重采样方法，将时间序列从一个频率转换至另一个频率的过程。

它主要有两种实现方式，分别是降采样和升采样，降采样指将高频率的数据转换为低频率，升采样则与其恰好相反，将低频率数据转换到高频率。

可以通过重采样解决数据样本不均衡的现象

标准化

数据标准化是指通过一定的方法和比例将数据映射到指定区间，根据使用函数的不同可以归纳为三类：直线型无量纲法、折线形无量纲法以及曲线型无量纲法。一些原始数据集是没有经过转化的有量纲数据，如果将其直接输入到模型中进行训练，受不同量纲特征的影响，会导致模型的收敛速度变慢，并且当特征量纲级别相差特别大时，模型可能会忽略掉量纲较小的特征而达不到理想效果。因此，在模型训练前，需要通过标准化方法将数据转换成无量纲数据，以消除量纲对模型产生的影响。

min-max标准化（归一化）

该方法是基于样本中的两个最值进行转换的，把最大值归为1，最小值归为0，其他值在其中分布。对于每个属性，设minA和maxA分别为属性A的最小值和最大值，将A的一个原始值x通过min-max标准化映射成在区间[0,1]中的值x’，其公式为：新数据=(原数据 - 最小值)/(最大值 - 最小值)

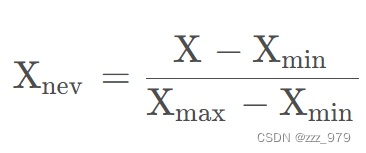
z-score标准化（规范化）

一般把均值归一化为0，方差归一化1。基于原始数据的均值（mean）和标准差（standarddeviation）进行数据的标准化。将A的原始值x使用z-score标准化到x’。z-score标准化方法适用于属性A的最大值和最小值未知的情况，或有超出取值范围的离群数据的情况，其公式为：新数据=(原数据-均值)/标准差

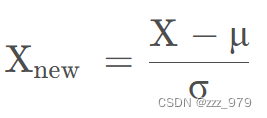
正则化

数据正则化是将样本的某个范数（如L1范数）缩放到到位1，正则化的过程是针对单个样本的，对于每个样本将样本缩放到单位范数

数据平滑

噪声是变量的随机误差和方差，是观测点和真实点之间的误差。

通常的处理办法：对数据进行分箱操作，等频或等宽分箱，然后用每个箱的平均数，中位数或者边界值（不同数据分布，处理方法不同）代替箱中所有的数，起到平滑数据的作用。

另外一种做法是，建立该变量和预测变量的回归模型，根据回归系数和预测变量，反解出自变量的近似值。

数据降维

PCA算法

在PCA中，数据从原来的坐标系转换到了新的坐标系，新坐标系的选择是由数据本身决定的。第一个新坐标轴选择的是原始数据中方差最大的方向，第二个新坐标轴的选择和第一个坐标轴正交且具有最大方差的方向。该过程一直重复，重复次数为原始数据中特征的数目。