---

39. 组合总和

教程视频：https://www.bilibili.com/video/BV1KT4y1M7HJ/?vd_source=ddffd51aa532d23e6feac69924e20891


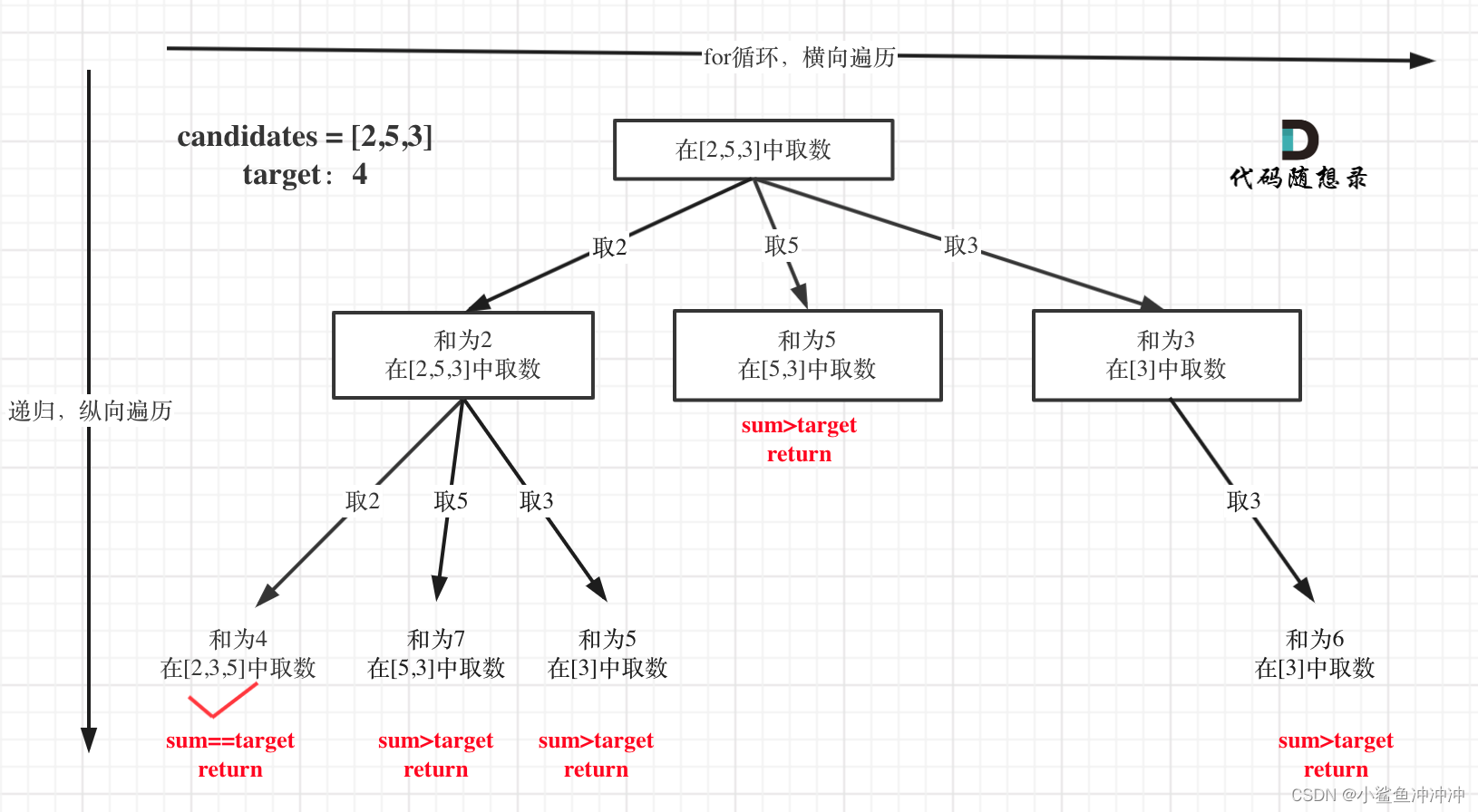
相比于之前的组合问题，本题树的深度取决于和是否超出target。

解法一：回溯

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    List<Integer> path = new ArrayList<>();

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        backtracking(candidates, target, 0, 0);
        return result;
    }
    public void backtracking(int[] candidates, int target, int sum,int startIndex){
        if(sum>target)return;
        if(sum==target){
            result.add(new ArrayList<>(path));
            return;
        }

        for(int i = startIndex ; i<candidates.length ; i++){
            sum+=candidates[i];
            path.add(candidates[i]);
            backtracking(candidates, target, sum, i);//因为可以重复,下一层从当前的第 i 个数字开始遍历
            sum-=candidates[i];
            path.remove(path.size()-1);
        }
    }
}

解法二：回溯+排序剪枝

对总集合排序之后，如果下一层的sum（就是本层的 sum + candidates[i]）已经大于target，就可以结束本轮for循环的遍历。

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    List<Integer> path = new ArrayList<>();

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates); // 剪枝操作1:先进行排序
        backtracking(candidates, target, 0, 0);
        return result;
    }
    public void backtracking(int[] candidates, int target, int sum,int startIndex){
        // 剪枝操作3:剪枝后大于的情况被剔除,不再需要终止条件if(sum>target)return;
        if(sum==target){
            result.add(new ArrayList<>(path));
            return;
        }

        // 剪枝操作2:如果当前sum和本层数据之和大于target,退出本层该数据后的遍历
        for(int i = startIndex ; i<candidates.length && sum + candidates[i] <= target ; i++){
            sum+=candidates[i];
            path.add(candidates[i]);
            backtracking(candidates, target, sum, i);//因为可以重复,下一层从当前的第 i 个数字开始遍历
            sum-=candidates[i];
            path.remove(path.size()-1);
        }
    }
}

---

40.组合总和II

教程视频：https://www.bilibili.com/video/BV12V4y1V73A/?spm_id_from=333.788&vd_source=ddffd51aa532d23e6feac69924e20891


【树枝去重】：candidates 中的每个数字在每个组合中只能使用 一次 。但本题中 candidates 包含重复元素，因此结果路径中可以用值相同的元素，只要它们对应的是candidates中的不同索引。因此向下伸展树枝时，每增一层，开始序号减一，这是树枝去重逻辑。
【数层去重】：在每层遍历中，如果同一树层上存在值相同的元素，它们中的第一个必定已经包含之后若干相同元素的所有分支，因此每层遍历的集合需要去重。

解法一：回溯（使用used标记数组）

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    List<Integer> path = new ArrayList<>();

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);//排序
        boolean[] used = new boolean[candidates.length];
        // System.out.println(used[0]);
        backtracking(candidates, target, 0, used);
        return result;
    }

    //startIndex表示每层遍历的起点，用于数层去重
    //used用于记录使用过的元素，可以判断组合是在树枝上还是数层上，用于保护树枝中值重复的情况
    public void backtracking(int[] candidates, int target,int startIndex, boolean[] used){
        if(target<0)return;
        if(target==0){
            result.add(new ArrayList<>(path));
            return;
        }

        for(int i=startIndex;i<candidates.length;i++){
            //树层去重
            if(i>0 && candidates[i]==candidates[i-1] && !used[i-1])continue;
            target-=candidates[i];
            path.add(candidates[i]);
            used[i]=true;
            backtracking(candidates,target,i+1,used);
            target+=candidates[i];
            path.remove(path.size()-1);
            used[i]=false;
        }

    }
}

解法一：回溯（不使用used标记数组）高效但更抽象

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    List<Integer> path = new ArrayList<>();

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);//剪枝1：排序
        backtracking(candidates, target, 0);
        return result;
    }

    //startIndex表示每层遍历的起点，用于数层去重
    //used用于记录使用过的元素，可以判断组合是在树枝上还是数层上，用于保护树枝中值重复的情况
    public void backtracking(int[] candidates, int target,int startIndex){
        // if(target<0)return;
        if(target==0){
            result.add(new ArrayList<>(path));
            return;
        }

        for(int i=startIndex;i<candidates.length && target-candidates[i]>=0;i++){
            //树层去重，跳过同一树层使用过的元素
            if(i>startIndex && candidates[i]==candidates[i-1])continue;
            target-=candidates[i];
            path.add(candidates[i]);
            backtracking(candidates,target,i+1);
            target+=candidates[i];
            path.remove(path.size()-1);
        }
    }
}

131.分割回文串

教程视频：https://www.bilibili.com/video/BV1c54y1e7k6/?spm_id_from=333.788&vd_source=ddffd51aa532d23e6feac69924e20891

这是一个切割问题，切割问题可以抽象为组合问题，用回溯法解决。
关于模拟切割线，其实就是index是上一层已经确定了的分割线，i是这一层试图寻找的新分割线

解法一：回溯

class Solution {
    List<List<String>> result = new ArrayList<>();
    List<String> path = new ArrayList<>();

    public List<List<String>> partition(String s) {
        backtracking(s, 0);
        return result;
    }

    public void backtracking(String s,int startIndex){
        //startIndex表示切割位置，如果切割位置等于s的大小，说明找到了一组分割方案
        if(startIndex==s.length()){
            result.add(new ArrayList<>(path));
            return;
        }

        for(int i=startIndex;i<s.length();i++){
            //判断是否是回文
            if(isPalindrome(s,startIndex,i)){
                //如果是回文子串，则记录
                path.add(s.substring(startIndex,i+1));
            }else{
                //如果不是回文串，剪去下层的递归，横向遍历同层的另一个数
                continue;
            }
            backtracking(s,i+1);
            path.remove(path.size()-1);
        }
    }

    //判断是否是回文串，区间是左闭右闭的
    public boolean isPalindrome(String s,int start,int end){
        while(start<end){
            if(s.charAt(start)!=s.charAt(end)){
                return false;
            }
            start++;
            end--;
        }
        return true;
    }
}

---

总结

1、在求和问题中，排序之后加剪枝是常见的套路！
2、组合总和II需要理清“树层去重”和“树枝去重”两个维度。
3、切割问题可以抽象为组合问题，用回溯法解决。关键在于用startIndex模拟分割线，确定递归终止条件。