目录
- 一、什么是堆?
- 1.1 大顶堆
- 1.2 小顶堆
- 1.3 自定义greater
- 1.4 堆索引的特点
- 1.5 堆操作
- 添加元素
- 删除最大元素
- 检查序列是否是堆
- 检查部分序列为堆
- 对堆进行排序
- 升序
- 降序
- 问题:sort()和sort_heap()有什么区别
- 二、排序算法:堆排序
- 2.1 堆排序原理
- 创建最大堆
- 堆排序(最大堆调整)
- 复杂度分析
- 2.2 堆排序代码实现
- 复杂度分析
- 三、堆排序应用
- 返回数组第k大元素
- 解法1:基于堆排序的选择方法
- 解法2:快速选择法
- 四、本文参考
一、什么是堆?
堆(heaps)不是容器,而是一种特别的数据组织方式。
1.1 大顶堆
父节点总是大于或等于子节点,这种情况下被叫作大顶堆。例如下图表示的大顶堆:
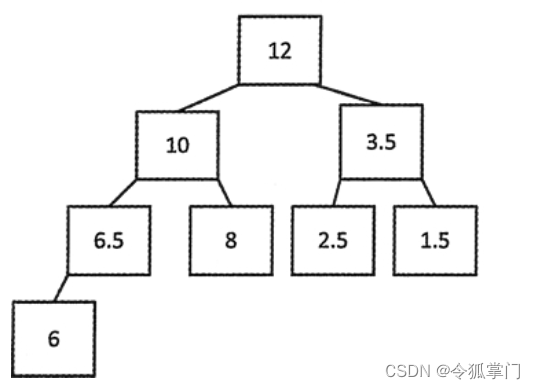
C++ STL中用来创建堆的函数定义在头文件 algorithm 中。max_heap() 对随机访问迭代器指定的一段元素重新排列,生成一个堆。默认可以生成一个大顶堆。例如下面的代码:
vector<double>nums1{ 2.5, 10.0, 3.5, 6.5, 8.0, 12.0, 1.5, 6.0 };
// 默认创建大顶堆
make_heap(nums1.begin(), nums1.end());
// Result: 12 10 3.5 6.5 8 2.5 1.5 6
for (auto ele : nums1) {
cout << ele << " ";
}
cout << endl;
1.2 小顶堆
父节点总是小于或等于子节点,这种情况下叫作小顶堆。例如下面的小顶堆:
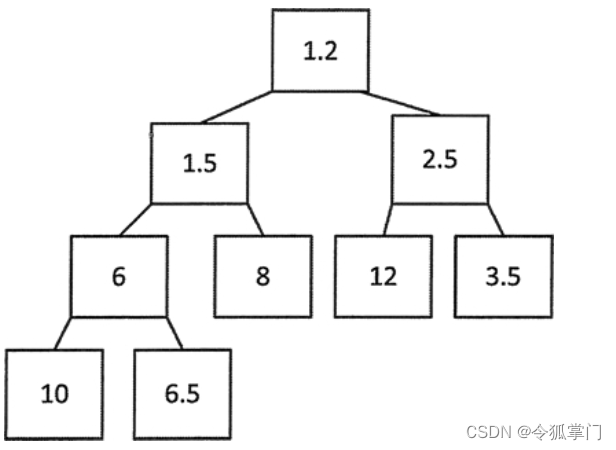
C++ STL创建小顶堆,需要使用std::greater<>(), 代码如下:
// 小顶堆
// 使用std::greater<>()创建小顶堆
vector<double> nums2{ 2.5, 10.0, 3.5, 6.5, 8.0, 12.0, 1.5, 6.0 };
make_heap(nums2.begin(), nums2.end(), std::greater<>());
for (auto ele : nums2) {
cout << ele << " ";
}
cout << endl;
1.3 自定义greater
基本数据类型默认可以进行大小比较,如果是其他数据类型,则需要自定义比较器,下面介绍如何自定义greater,可以看看greater的定义:
template <>
struct greater<void> {
template <class _Ty1, class _Ty2>
_NODISCARD constexpr auto operator()(_Ty1&& _Left, _Ty2&& _Right) const
noexcept(noexcept(static_cast<_Ty1&&>(_Left) > static_cast<_Ty2&&>(_Right))) // strengthened
-> decltype(static_cast<_Ty1&&>(_Left) > static_cast<_Ty2&&>(_Right)) {
return static_cast<_Ty1&&>(_Left) > static_cast<_Ty2&&>(_Right);
}
using is_transparent = int;
};
当然也有less,代码如下:
template <>
struct less<void> {
template <class _Ty1, class _Ty2>
_NODISCARD constexpr auto operator()(_Ty1&& _Left, _Ty2&& _Right) const
noexcept(noexcept(static_cast<_Ty1&&>(_Left) < static_cast<_Ty2&&>(_Right))) // strengthened
-> decltype(static_cast<_Ty1&&>(_Left) < static_cast<_Ty2&&>(_Right)) {
return static_cast<_Ty1&&>(_Left) < static_cast<_Ty2&&>(_Right);
}
using is_transparent = int;
};
下面提供自定义greater的方法,代码如下:
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
struct Student {
int id;
string name;
int score;
Student(int _id, string _name, int _score)
:id(_id), name(_name), score(_score) {}
};
struct cmp {
bool operator() (Student a, Student b) {
return a.score > b.score;
}
};
int main()
{
Student s1(1001, "zhangsan", 97);
Student s2(1005, "wangwu", 85);
Student s3(1003, "luban", 98);
Student s4(1002, "lier", 99);
Student s5(1007, "tianqi", 63);
Student s6(1009, "zhaoliu", 56);
Student s7(1006, "jack", 71);
Student s8(1010, "houyi", 30);
Student s9(1008, "gongben", 84);
vector<Student> stu{ s1, s2, s3, s4, s5, s6, s7, s8, s9 };
make_heap(stu.begin(), stu.end(), cmp());
for (auto ele : stu) {
cout << ele.score << " ";
}
cout << endl;
return 0;
}
运行结果:
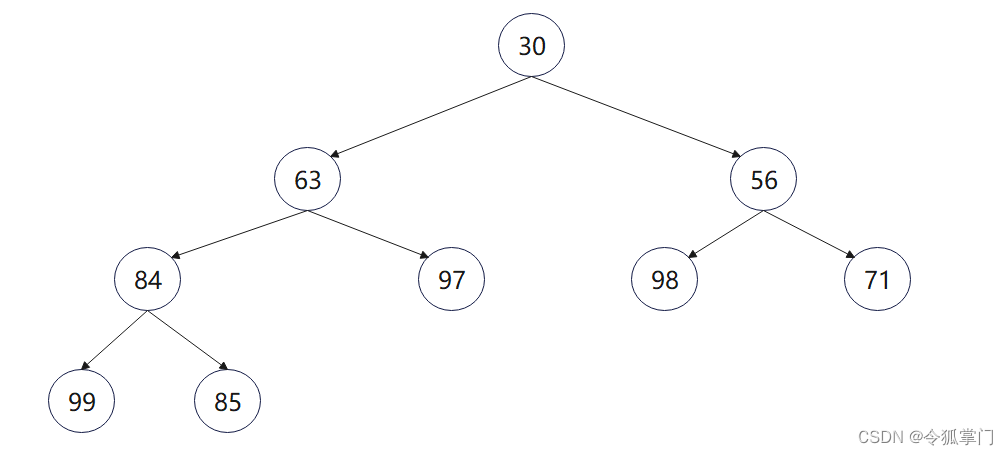
30 63 56 84 97 98 71 99 85
堆结构如下图:
1.4 堆索引的特点
下标为 i 的结点的父结点下标为(i-1)/2;其左右子结点分别为 (2i + 1)、(2i + 2)
注意:该特性很重要,这是堆代码实现的依据
1.5 堆操作
添加元素
比如往nums1里面push元素
nums1.push_back(11); // Result: 12 10 3.5 6.5 8 2.5 1.5 6 11
std::push_heap(nums1.begin(), nums1.end());
代码说明
push_back() 会在序列末尾添加元素,然后使用 push_heap() 恢复堆的排序。通过调用 push_heap(),释放了一个信号,指出我们向堆中添加了一个元素,这可能会导致堆排序的混乱。push_heap() 会因此认为最后一个元素是新元素,为了保持堆结构,会重新排列序列。
注意:如果 push_heap() 和 make_heap() 的第 3 个参数不同,代码就无法正常执行。
删除最大元素
代码
// 删除最大元素
std::pop_heap(nums1.begin(), nums1.end());
// Result:10 8 3.5 6.5 6 2.5 1.5 12
nums1.pop_back();// Result:10 8 3.5 6.5 6 2.5 1.5
代码说明
pop_heap() 函数将第一个元素移到最后,并保证剩下的元素仍然是一个堆。然后就可以使用 vector 的成员函数 pop_back() 移除最后一个元素。如果 make_heap() 中用的是自己的比较函数,那么 pop_heap() 的第 3 个参数也需要是这个函数:
检查序列是否是堆
使用is_heap()方法判断是否是堆
if (std::is_heap(nums1.begin(), nums1.end()))
std::cout << "Great! We still have a heap.\n";
else
std::cout << "oh bother! We messed up the heap.\n";
如果元素段是堆,那么 is_heap() 会返回 true。这里是用默认的比较断言 less<> 来检查元素顺序。如果这里使用的是用 greater<> 创建的堆,就会产生错误的结果。为了得到正确的结果,表达式需要写为:
if (std::is_heap(nums2.begin(), nums2.end(), std::greater<>()))
{
cout << "nums2是小堆" << endl;
}
else
{
cout << "nums2不是小堆" << endl;
}
检查部分序列为堆
可以使用std::is_heap_until来检查,是否有部分序列为堆
std::vector<double> numbers{ 2.5, 10.0, 3.5, 6.5, 8.0, 12.0, 1.5, 6.0 };
std::make_heap(std::begin(numbers), ::end(numbers), std::greater<>());
// Result: 1.5 6 2.5 6.5 8 12 3.5 10
std::pop_heap(std::begin(numbers), std::end(numbers), std::greater<>());
// Result: 2.5 6 3.5 6.5 8 12 10 1.5
auto iter = std::is_heap_until(std::begin(numbers), std::end(numbers), std::greater<>());
if (iter != std::end(numbers))
std::cout << "numbers is a heap up to " << *iter << std::endl;
is_heap_until() 函数返回一个迭代器,指向第一个不在堆内的元素。这个代码段会输出最后一个元素的值 1.5,因为在调用 pop_heap() 后,这个元素就不在堆内了。如果整段元素都是堆,函数会返回一个结束迭代器,因此if语句可以确保我们不会解引用一个结束迭代器。如果这段元素少于两个,也会返回一个结束迭代器。这里还有另一个版本的 is_heap_until(),它有两个参数,以 less<> 作为默认断言。
对堆进行排序
升序
STL 提供的最后一个操作是 sort_heap(),它会将元素段作为堆来排序。如果元素段不是堆,程序会在运行时崩溃。这个函数有以两个迭代器为参数的版本,迭代器指向一个假定的大顶堆(用 less<> 排列),然后将堆中的元素排成降序。结果当然不再是大顶堆。下面是一个使用它的示例:
std::vector<double> numbers {2.5, 10.0, 3.5, 6.5, 8.0, 12.0, 1.5, 6.0};
std::make_heap(std::begin(numbers), std::end(numbers));
//Result: 12 10 3.5 6.5 8 2.5 1.5 6
std::sort_heap(std::begin(numbers), std::end(numbers));
// Result: 1.5 2.5 3.5 6 6.5 8 10 12
排序操作的结果不是一个大顶堆,而是一个小顶堆。
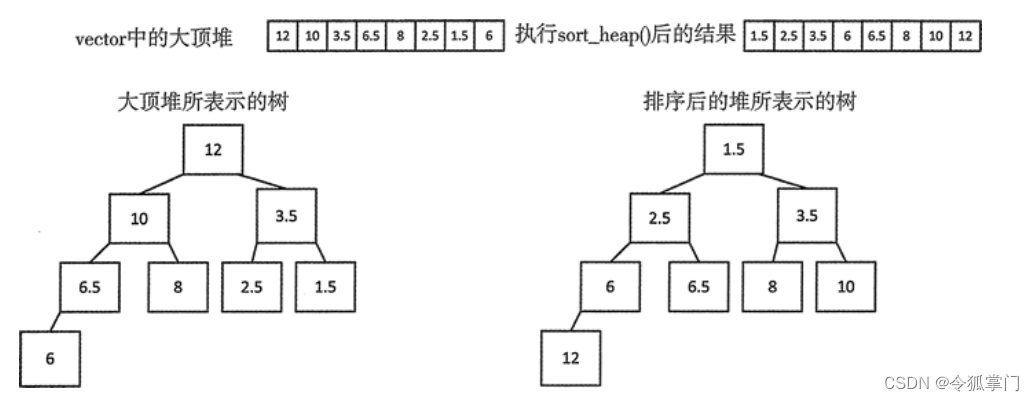
注意:尽管堆并不是全部有序的,但任何全部有序的序列都是堆。
降序
第 2 个版本的 sort_heap() 有第 3 个参数,可以指定一个用来创建堆的断言。如果用断言 greater() 来创建堆,会生成一个小顶堆,对它进行排序会生成一个降序序列。对小顶堆执行 sort_heap() 后,会变成一个大顶堆。
std::vector<double> numbers {2.5, 10.0, 3.5, 6.5, 8.0, 12.0, 1.5, 6.0};
std::make_heap(std::begin(numbers), std::end(numbers),std::greater<>());
// Result: 1.5 6 2.5 6.5 8 12 3.5 10
std::sort_heap(std::begin(numbers), std::end(numbers),std::greater<>());
// Result: 12 10 8 6.5 6 3.5 2.5 1.5
问题:sort()和sort_heap()有什么区别
我们知道可以用定义在 algorithm 头文件中的函数模板 sort() 来对堆排序,那么为什么还需要 sort_heap() 函数?sort_heap() 函数可以使用特殊的排序算法,巧合的是它被叫作堆排序。这个算法首先会创建一个堆,然后充分利用数据的局部有序性对数据进行排序。sort_heap 认为堆总是存在的,所以它只做上面的第二步操作。充分利用堆的局部有序性可以潜在地使排序变得更快,尽管这可能并不是一直有用。
二、排序算法:堆排序
2.1 堆排序原理
堆排序,需要创建堆,下面介绍如何创建堆
假设给定一个组无序数列{100,5,3,11,6,8,7},带着问题,我们对其进行堆排序操作进行分步操作说明。

创建最大堆
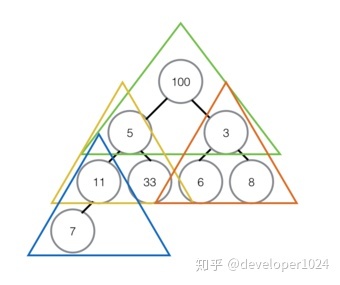
①首先我们将数组我们将数组从上至下按顺序排列,转换成二叉树:一个无序堆。每一个三角关系都是一个堆,上面是父节点,下面两个分叉是子节点,两个子节点俗称左孩子、右孩子;
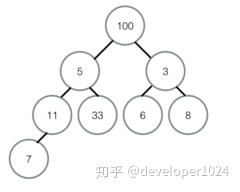
②转换成无序堆之后,我们要努力让这个无序堆变成最大堆(或是最小堆),即每个堆里都实现父节点的值都大于任何一个子节点的值。

③从最后一个堆开始,即左下角那个没有右孩子的那个堆开始;首先对比左右孩子,由于这个堆没有右孩子,所以只能用左孩子,左孩子的值比父节点的值小所以不需要交换。如果发生交换,要检测子节点是否为其他堆的父节点,如果是,递归进行同样的操作。
④第二次对比红色三角形内的堆,取较大的子节点,右孩子8胜出,和父节点比较,右孩子8大于父节点3,升级做父节点,与3交换位置,3的位置没有子节点,这个堆建成最大堆。
⑤对黄色三角形内堆进行排序,过程和上面一样,最终是右孩子33升为父节点,被交换的右孩子下面也没有子节点,所以直接结束对比。
⑥最顶部绿色的堆,堆顶100比左右孩子都大,所以不用交换,至此最大堆创建完成。
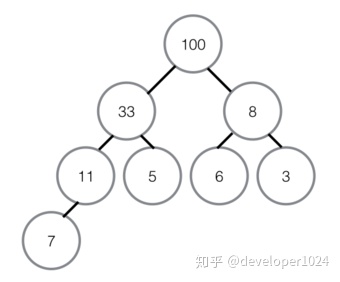
堆排序(最大堆调整)
①首先将堆顶元素100交换至最底部7的位置,7升至堆顶,100所在的底部位置即为有序区,有序区不参与之后的任何对比。
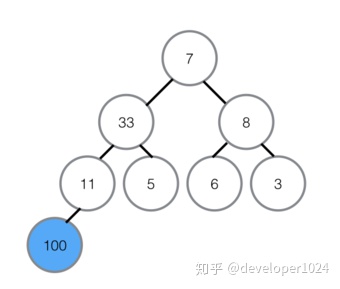
②在7升至顶部之后,对顶部重新做最大堆调整,左孩子33代替7的位置。
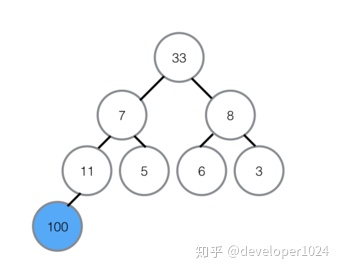
③在7被交换下来后,下面还有子节点,所以需要继续与子节点对比,左孩子11比7大,所以11与7交换位置,交换位置后7下面为有序区,不参与对比,所以本轮结束,无序区再次形成一个最大堆。
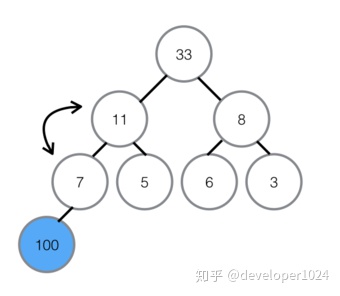
④将最大堆堆顶33交换至堆末尾,扩大有序区;
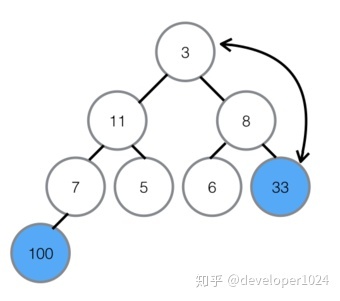
⑤不断建立最大堆,并且扩大有序区,最终全部有序。
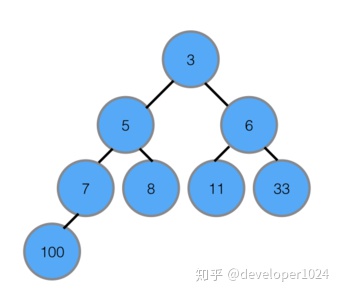
复杂度分析
- 平均时间复杂度:O(nlogn)
- 最佳时间复杂度:O(nlogn)
- 最差时间复杂度:O(nlogn)
- 稳定性:不稳定
堆排序其实也是一种选择排序,是一种树形选择排序。只不过直接选择排序中,为了从R[1…n]中选择最大记录,需比较n-1次,然后从R[1…n-2]中选择最大记录需比较n-2次。事实上这n-2次比较中有很多已经在前面的n-1次比较中已经做过,而树形选择排序恰好利用树形的特点保存了部分前面的比较结果,因此可以减少比较次数。对于n个关键字序列,最坏情况下每个节点需比较log2(n)次,因此其最坏情况下时间复杂度为nlogn。堆排序为不稳定排序,不适合记录较少的排序。
2.2 堆排序代码实现
/*
堆排序
堆的特点
一般用数组来表示堆,下标为 i 的结点的父结点下标为(i-1)/2;其左右子结点分别为 (2i + 1)、(2i + 2)
链接
*/
#include <iostream>
#include <algorithm>
using namespace std;
class Solution
{
private:
void max_heapify(int arr[], int start, int end)
{
//建立父节点指标和子节点指标
int dad = start; // 父节点
int son = dad * 2 + 1; // 左边子节点
while (son <= end) { //若子节点指标在范围内才做比较
if (son + 1 <= end && arr[son] < arr[son + 1]) //先比较两个子节点大小,选择最大的
son++;
if (arr[dad] > arr[son]) //如果父节点大于子节点代表调整完毕,直接跳出函数
return;
else
{
//否则交换父子内容再继续子节点和孙节点比较
swap(arr[dad], arr[son]);
dad = son;
son = dad * 2 + 1;
}
}
}
public:
void heap_sort(int arr[], int len) {
//初始化,i从最后一个父节点开始调整
for (int i = len / 2 - 1; i >= 0; i--)
max_heapify(arr, i, len - 1);
//先将第一个元素和已经排好的元素前一位做交换,再从新调整(刚调整的元素之前的元素),直到排序完毕
for (int i = len - 1; i > 0; i--) {
swap(arr[0], arr[i]);
max_heapify(arr, 0, i - 1);
}
}
};
int main() {
int arr[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };
int len = (int)sizeof(arr) / sizeof(*arr);
Solution s;
s.heap_sort(arr, len);
for (int i = 0; i < len; i++)
cout << arr[i] << ' ';
cout << endl;
return 0;
}
复杂度分析
- 平均时间复杂度:O(nlogn)
- 最佳时间复杂度:O(nlogn)
- 最差时间复杂度:O(nlogn)
- 稳定性:不稳定
三、堆排序应用
返回数组第k大元素
这是leetcode第215题, 给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入: [3,2,1,5,6,4], k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4
提示:
1 <= k <= nums.length <= 105
-104 <= nums[i] <= 104
解法1:基于堆排序的选择方法
思路和算法
我们也可以使用堆排序来解决这个问题——建立一个大根堆,做 k−1 次删除操作后堆顶元素就是我们要找的答案。在很多语言中,都有优先队列或者堆的的容器可以直接使用,但是在面试中,面试官更倾向于让更面试者自己实现一个堆。所以建议读者掌握这里大根堆的实现方法,在这道题中尤其要搞懂「建堆」、「调整」和「删除」的过程。
class Solution {
private:
void maxHeapify(vector<int>& a, int i, int heapSize) {
int l = i * 2 + 1, r = i * 2 + 2, largest = i;
if (l < heapSize && a[l] > a[largest]) {
largest = l;
}
if (r < heapSize && a[r] > a[largest]) {
largest = r;
}
if (largest != i) {
swap(a[i], a[largest]);
maxHeapify(a, largest, heapSize);
}
}
void buildMaxHeap(vector<int>& a, int heapSize) {
for (int i = heapSize / 2; i >= 0; --i) {
maxHeapify(a, i, heapSize);
}
}
public:
int findKthLargest(vector<int>& nums, int k) {
int heapSize = nums.size();
buildMaxHeap(nums, heapSize);
for (int i = nums.size() - 1; i >= nums.size() - k + 1; --i) {
swap(nums[0], nums[i]);
--heapSize;
maxHeapify(nums, 0, heapSize);
}
return nums[0];
}
};
复杂度分析
时间复杂度:O(nlogn),建堆的时间代价是 O(n),删除的总代价是 O(klogn),因为 k<n,故渐进时间复杂为 O(n+klogn)=O(nlogn)。
空间复杂度:O(logn),即递归使用栈空间的空间代价。
解法2:快速选择法
基于快速排序的选择方法
思路和算法
我们可以用快速排序来解决这个问题,先对原数组排序,再返回倒数第 k个位置,这样平均时间复杂度是 O(nlogn),但其实我们可以做的更快。
首先我们来回顾一下快速排序,这是一个典型的分治算法。我们对数组 a[l⋯r] 做快速排序的过程是(参考《算法导论》):
分解: 将数组 a[l⋯r] 「划分」成两个子数组 a[l⋯q−1]、a[q+1⋯r],使得 a[l⋯q−1] 中的每个元素小于等于 a[q],a[q] 小于等于 a[q + 1 a[q+1⋯r] 中的每个元素。其中,计算下标 q 也是「划分」过程的一部分。
解决: 通过递归调用快速排序,对子数组 a[l⋯q−1] 和 a[q+1⋯r] 进行排序。
合并: 因为子数组都是原址排序的,所以不需要进行合并操作,a[l⋯r] 已经有序。
上文中提到的 「划分」 过程是:从子数组 a[l⋯r] 中选择任意一个元素 x 作为主元,调整子数组的元素使得左边的元素都小于等于它,右边的元素都大于等于它, x 的最终位置就是 q。
由此可以发现每次经过「划分」操作后,我们一定可以确定一个元素的最终位置,即 x 的最终位置为 q,并且保证 a[l⋯q−1] 中的每个元素小于等于 a[q],且 a[q] 小于等于 a[q+1⋯r] 中的每个元素。所以只要某次划分的 q 为倒数第 k 个下标的时候,我们就已经找到了答案。 我们只关心这一点,至于 a[l⋯q−1] 和 a[q+1⋯r] 是否是有序的,我们不关心。
因此我们可以改进快速排序算法来解决这个问题:在分解的过程当中,我们会对子数组进行划分,如果划分得到的 qq 正好就是我们需要的下标,就直接返回 a[q];否则,如果 q 比目标下标小,就递归右子区间,否则递归左子区间。这样就可以把原来递归两个区间变成只递归一个区间,提高了时间效率。这就是「快速选择」算法。
我们知道快速排序的性能和「划分」出的子数组的长度密切相关。直观地理解如果每次规模为 n 的问题我们都划分成 1 和 n−1,每次递归的时候又向 n−1 的集合中递归,这种情况是最坏的,时间代价是 O(n^2) 。我们可以引入随机化来加速这个过程,它的时间代价的期望是 O(n),证明过程可以参考「《算法导论》9.2:期望为线性的选择算法」。
代码
class Solution {
private:
int quickSelect(vector<int>& a, int l, int r, int index) {
int q = randomPartition(a, l, r);
if (q == index) {
return a[q];
} else {
return q < index ? quickSelect(a, q + 1, r, index) : quickSelect(a, l, q - 1, index);
}
}
inline int randomPartition(vector<int>& a, int l, int r) {
int i = rand() % (r - l + 1) + l;
swap(a[i], a[r]);
return partition(a, l, r);
}
inline int partition(vector<int>& a, int l, int r) {
int x = a[r], i = l - 1;
for (int j = l; j < r; ++j) {
if (a[j] <= x) {
swap(a[++i], a[j]);
}
}
swap(a[i + 1], a[r]);
return i + 1;
}
public:
int findKthLargest(vector<int>& nums, int k) {
srand(time(0));
return quickSelect(nums, 0, nums.size() - 1, nums.size() - k);
}
};
复杂度分析
时间复杂度:O(n),如上文所述,证明过程可以参考「《算法导论》9.2:期望为线性的选择算法」。
空间复杂度:O(logn),递归使用栈空间的空间代价的期望为 O(logn)。
四、本文参考
参考1:https://blog.csdn.net/qq_22642239/article/details/102824586
参考2:https://leetcode.cn/problems/kth-largest-element-in-an-array
参考3:https://zhuanlan.zhihu.com/p/124885051