文章目录
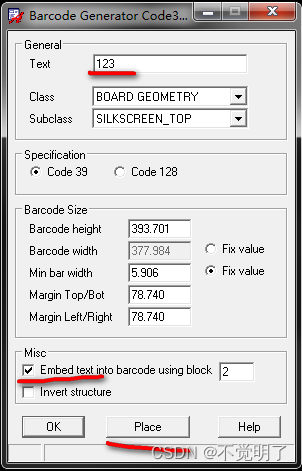
- 👍 AVL树的概念先了解一下
- 😁AVL树节点的定义
- 😊AVL树插入节点
- 🤞AVL树为什么要旋转
- 😍AVL树的四种旋转
- 左单旋
- 右单旋
- 左右双旋
- 右左双旋
- ❤️结语
关于AVL树的讲解
👍 AVL树的概念先了解一下
- 它的左右子树都是AVL树
- 左右子树高度之差(简称平衡因子)的
绝对值不超过1 (-1/0/1)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MlyXcMxn-1668154168392)(https://p6-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/6905b990ac694ebab9a03d2a44f0c8a7~tplv-k3u1fbpfcp-watermark.image?)]](https://img-blog.csdnimg.cn/eda1fa91c8624a41866ec284852dc918.png)
- 如果一棵二叉搜索树是高度平衡的,它就是AVL树。如果它有n个结点,其高度可保持在 O ( l o g 2 n ) O(log_2 n) O(log2n),搜索时间复杂度O( l o g 2 n log_2 n log2n)。
😁AVL树节点的定义
//AVL 树的节点
template<class K, class V>
struct AVLTreeNode
{
pair<K, V> _kv;
AVLTreeNode<K, V>* _left;
AVLTreeNode<K, V>* _right;
AVLTreeNode<K, V>* _parent;
//左右子数的高度差
int _bf;
AVLTreeNode(const pair<K, V>& kv)
:_kv(kv)
,_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
, _bf(0)
{}
};
😊AVL树插入节点
bool Insert(const pair<K, V>& kv)
{
// 1、搜索树的规则插入
// 2、看是否违反平衡规则,如果违反就需要处理:旋转
if (_root == nullptr)
{
_root = new Node(kv);
_root->_bf = 0;
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
// ...
// 更新平衡因子
while (parent) // 最远要更新根
{
if (cur == parent->_right)
{
parent->_bf++;
}
else
{
parent->_bf--;
}
// 是否继续更新?
if (parent->_bf == 0) // 1 or -1 -》 0 插入节点填上矮的那边
{
// 高度不变,更新结束
break;
}
else if (parent->_bf == 1 || parent->_bf == -1)
// 0 -》 1 或 -1 插入节点导致一边变高了
{
// 子树的高度变了,继续更新祖先
cur = cur->_parent;
parent = parent->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2)
// -1 or 1 -》 2 或 -2 插入节点导致本来高一边又变高了
{
// 子树不平衡 -- 需要旋转处理
if (parent->_bf == 2 && cur->_bf == 1) // 左单旋
{
RotateL(parent);
}
else if (parent->_bf == -2 && cur->_bf == -1) // 右单旋
{
RotateR(parent);
}
else if (parent->_bf == -2 && cur->_bf == 1) // 左右双旋
{
RotateLR(parent);
}
else if (parent->_bf == 2 && cur->_bf == -1) // 右左双旋
{
RotateRL(parent);
}
break;
}
else
{
// 插入之前AVL就存在不平衡子树,|平衡因子| >= 2的节点
assert(false);
}
}
return true;
}
🤞AVL树为什么要旋转
当一个树左右高度差绝对值大于1 的时候就要进行旋转
这是一个简单的示范:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fmbnuLF2-1668154168393)(https://p9-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/c39f842b8f704cccba14a58aa95ab270~tplv-k3u1fbpfcp-watermark.image?)]](https://img-blog.csdnimg.cn/749d8500790b42f4a1ba17cefcc27db7.png)
😍AVL树的四种旋转
左单旋
图片演示(我自己纯手画):

代码:
void RotateL(Node* parent)//左单旋
{
Node* SubR = parent->_right;
Node* SubRL = SubR->_left;
parent->_right = SubRL;
if (SubRL)
{
SubRL->_parent = parent;
}
Node* ppNode = parent->_parent;
SubR->_left = parent;
parent->_parent = SubR;
if (_root == parent)
{
_root = SubR;
_root->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = SubR;
}
else
{
ppNode->_right = SubR;
}
SubR->_parent = ppNode;
}
//旋转结束更新平衡因子
parent->_bf = 0;
SubR->_bf = 0;
}
右单旋
图片演示(我纯手画)

代码:
void RotateR(Node* parent)//右单旋
{
Node* SubL = parent->_left;
Node* SubLR = SubL->_right;
parent->_left = SubLR;
if (SubLR)
{
SubLR->_parent = parent;
}
Node* ppNode = parent->_parent;
SubL->_right = parent;
parent->_parent = SubL;
if (_root == parent)
{
_root = SubL;
_root->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = SubL;
}
else
{
ppNode->_right = SubL;
}
SubL->_parent = ppNode;
}
//旋转结束更新平衡因子
parent->_bf = 0;
SubL->_bf = 0;
}
左右双旋
图片演示(我纯手画):

parent节点平衡因子和subL节点的平衡因子都与subLR有关
| subLR | parent | subL |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | -1 |
| -1 | 1 | 0 |
代码:
void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->_bf;
RotateL(parent->_left);
RotateR(parent);
// 更新平衡因子
if (bf == 0)
{
parent->_bf = 0;
subL->_bf = 0;
subLR->_bf = 0;
}
else if (bf == 1)
{
parent->_bf = 0;
subL->_bf = -1;
subLR->_bf = 0;
}
else if (bf == -1)
{
parent->_bf = 1;
subL->_bf = 0;
subLR->_bf = 0;
}
else
{
// subLR->_bf旋转前就有问题
assert(false);
}
}
右左双旋
图片演示(我自己纯手画):

e?)]
parent节点平衡因子和subR节点的平衡因子都与subRL有关
| subRL | parent | subR |
|---|---|---|
| 0 | 0 | 0 |
| 1 | -1 | 0 |
| -1 | 0 | 1 |
代码:
void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
RotateR(parent->_right);
RotateL(parent);
if (bf == 0)
{
subRL->_bf = 0;
parent->_bf = 0;
subR->_bf = 0;
}
else if (bf == 1)
{
subRL->_bf = 0;
parent->_bf = -1;
subR->_bf = 0;
}
else if (bf == -1)
{
subRL->_bf = 0;
parent->_bf = 0;
subR->_bf = 1;
}
else
{
// subLR->_bf旋转前就有问题
assert(false);
}
}
❤️结语
一起加油