Rust机器学习之ndarray
众所周知,Python之所以能成为机器学习的首选语言,与其丰富易用的库有很大关系。某种程度上可以说是诸如numpy、pandas、scikit-learn、matplotlib、pytorch、networks…等一系列科学计算和机器学习库成就了Python今天编程语言霸主的地位。基本上今天的机器学习任务主要就建立在上面列举的这6个库上。这6个库在Rust上都有对应的替代方案,从本章开始,我会带大家一起学习如何使用Rust及其库替代Python来更好得完成机器学习任务。
| Python库 | Rust替代方案 | 教程 |
|---|---|---|
numpy | ndarray | Rust机器学习之ndarray |
pandas | Polars | Rust机器学习之Polars |
scikit-learn | Linfa Smartcore | Rust机器学习之Linfa |
pytorch | tch-rs | Rust机器学习之tch-rs |
networks | petgraph | Rust机器学习之petgraph |
matplotlib | plotters | Rust机器学习之plotters |
数据和算法工程师偏爱Jupyter,为了跟Python保持一致的工作环境,文章中的示例都运行在Jupyter上。因此需要各位搭建Rust交互式编程环境(让Rust作为Jupyter的内核运行在Jupyter上),相关教程请参考 Rust交互式编程环境搭建
ndarray是个啥?
ndarray是Rust生态中用于处理数组的库。它包含了所有常用的数组操作。简单地说ndarray相当于Rust的numpy。
除了数组操作,ndarray还通过派生包提供其他丰富功能,比如
- ndarray-linalg 用于线性代数运算;
- ndarray-rand 用于产生随机数;
- ndarray-stats 用于统计计算;
可以说ndaary不但包含了numpy的功能,还包含了部分scipy的功能。
值得一提的是,ndarray还很好地支持很多外部特性。比如可以支持 rayon做并行计算,支持BLAS进行底层运算加速。因此ndarray的性能非常彪悍。
ndarray 的 BLAS是通过 blas-src 实现的,
blas-src为ndarray提供可选的BLAS源,目前支持
accelerate- 苹果的Accelerate 框架(仅支持Mac系统)blis- BLIS是一个类BLAS高性能线性代数库intel-mkl- Intel-MKL是⼀套经过高度优化和广泛线程化的数学库netlib- Netlib是一系列数学工具的集合,其中包含BLAS和LAPACK实现openblas- OpenBLAS是一套高度优化的开源BLAS库
为啥要用ndarray?
Rust本身已经自带了数组(或列表)类型,也有vector容器。得益于Rust自身的强大,这些自带的数据类型或容器比很多其他编程语言都要快,甚至快一个数量级。那么我们为什么还需要ndarray呢?
首先,ndarray是专门为处理n维数组(矩阵)而设计的,里面包含了很多数学运算,比如矩阵相乘、矩阵求逆等。
其次,ndarray支持SIMD(Single Instruction Multiple Data),可以进一步提升计算性能。
SIMD 的全称是 Single Instruction Multiple Data,中文名“单指令多数据”。顾名思义,一条指令处理多个数据。
如上图所示
(a) 是普通的标量计算,加法指令一次只能对两个数执行一个加法操作。
(b)是SIMD向量计算,SIMD加法指令一次可以对两个数组(向量)执行加法操作。
ndarray简明教程
看了上面的介绍我猜你已经迫不及待想尝试一下ndarray的威力了。下面我们开始ndarray的学习。
首先让我们引入ndarray包。
传统的Rust程序有Cargo进行包管理,只需要在cargo.toml的[dependencies]中加入
ndarray = "0.15.6"
然后在main.rs开头加入
use ndarray::prelude::*;
即可引入ndarray。prelude涵盖了几乎一切我们需要的模块。
但是在交互环境下没有Cargo,我们需要用evcxr的:dep命令来引入包。在Jupyter中输入如下代码:
:dep ndarray = {version = "0.15.6"}
use ndarray::prelude::*;
创建数组
我们先来看一下如何创建数组:
let arr = array![1., 2., 3., 4., 5., 6.];
println!("1D array: {}", arr);
ndarray提供了array!宏来创建数组。array!宏会自动判断创建那种类型的ArrayBase。上面的示例代码创建了一个1-D类型的ArrayBase,即一维数组。基类ArrayBase实现了std::fmt::Display方法,因此创建的对象可以直接利用println!宏输出。
我们比较一下ndarray与rust自带数组和vec的区别:
let arr1 = array![1., 2., 3., 4., 5., 6.];
println!("1D array: \t{}", arr1);
let ls1 = [1., 2., 3., 4., 5., 6.];
println!("1D list: \t{:?}", ls1);
let vec1 = vec![1., 2., 3., 4., 5., 6.];
println!("1D vector: \t{:?}", vec1);
输出结果如下:
1D array: [1, 2, 3, 4, 5, 6]
1D list: [1.0, 2.0, 3.0, 4.0, 5.0, 6.0]
1D vector: [1.0, 2.0, 3.0, 4.0, 5.0, 6.0]
注意,array!将浮点型转成了整形,因为给定的数小数位都为0。
向量加法
下面我们让两个数组中的元素两两相加:
let arr2 = array![1., 2.2, 3.3, 4., 5., 6.];
let arr3 = arr1 + arr2;
println!("1D array: \t{}", arr3);
对比Rust自带数组和vec的实现,你就能发现ndarray多么简单自然。
let arr2 = array![1., 2.2, 3.3, 4., 5., 6.];
let arr3 = arr1 + arr2;
println!("1D array: \t{}", arr3);
let ls2 = [1., 2.2, 3.3, 4., 5., 6.];
let mut ls3 = ls1.clone();
for i in 1..ls2.len(){
ls3[i] = ls1[i] + ls2[i];
}
println!("1D list: \t{:?}", ls3);
let vec2 = vec![1., 2.2, 3.3, 4., 5., 6.];
let vec3: Vec<f64> = vec1.iter().zip(vec2.iter()).map(|(&e1, &e2)| e1 + e2).collect();
println!("1D vec: \t{:?}", vec3);
输出结果:
1D array: [2, 4.2, 6.3, 8, 10, 12]
1D list: [1.0, 4.2, 6.3, 8.0, 10.0, 12.0]
1D vec: [2.0, 4.2, 6.3, 8.0, 10.0, 12.0]
上面的对比可以发现,Rust自带数组和vec都需要循环或迭代逐个元素相加求值,而ndarray只需要简单的+即可,即简单又直观。对数据和算法工程师来说,ndarray可以极大提高开发效率。
二维数组和高维数组
接下来的演示就不再给大家比较Rust自带数组和vec的实现了。上一节已经充分说明用Rust自带数据类型和数据结构来实现数组操作非常繁琐,而ndarray则十分简洁直观。所以下面我们将聚集ndarray。
ndarray提供多种方法创建和实例化二维数组。看下面代码:
let arr4 = array![[1., 2., 3.], [ 4., 5., 6.]];
let arr5 = Array::from_elem((2, 1), 1.);
let arr6 = arr4 + arr5;
println!("2D array:\n{}", arr6);
输出如下:
2D array:
[[2, 3, 4],
[5, 6, 7]]
上面代码展示了2种创建二维数组的方法。
array!宏需要指定数组中的所有元素Array::from_elem需要我们给定Shape(在上面案例中是(2,1))和填充元素(在上面案例中是1.0),该方法会用给定元素填充指定大小的二维数组
ndarray还提供了快速创建常用二维数组(矩阵)的方法。看下面代码:
let arr7 = Array::<f64, _>::zeros(arr6.raw_dim());
let arr8 = arr6 * arr7;
println!("{}", arr8);
输出:
[[0, 0, 0],
[0, 0, 0]]
Array::zeros(Shape)用0填充指定Shape大小的矩阵。
这里的<f64, _>要解释一下,因为Rust有着严格的类型,编译器有时无法通过0推断出数据类型,所以需要我们显式地告诉编译器这里填充的数据是什么类型。后面的_表示让编译器推断这里的数据类型,此处的数据类型是Shape。
.raw_dim()方法我想你已经猜到了它的作用,没错,就是返回矩阵的维度(dimension)。
在线性代数和机器学习中经常会用到单位矩阵(主对角线元素为1,其余元素为0的二维矩阵)。ndarray提供了专门的eye方法来生成单位矩阵。请看下面的代码:
let identity: Array2<f64> = Array::eye(3);
println!("\n{}", identity);
输出:
[[1, 0, 0],
[0, 1, 0],
[0, 0, 1]]
eye方法需要我们传入矩阵大小,因为单位矩阵一定是方阵,所以只需要传一个整数即可。这里要注意的是identity的类型我们明确定义为Array2类型,Array2是ArrayBase子类,表示一个二位数组。
单位矩阵(数学上一般用 I I I表示)有很多性质,比如任何矩阵乘以单位矩阵都等于它本身: A ⋅ I = A = I ⋅ A A · I = A = I · A A⋅I=A=I⋅A,就像我们经典代数中的1一样。我们可以验证一下单位矩阵的这个性质。
let arr9 = array![[1., 2., 3.], [ 4., 5., 6.], [7., 8., 9.]];
let arr10 = arr9 * identity;
println!("{}", arr10);
结果输出:
[[1, 0, 0],
[0, 5, 0],
[0, 0, 9]]
输出结果似乎不是arr9本身。这是因为矩阵运算中*和·不是一回事。*也叫标量乘法,是将两个矩阵对应位置元素相乘。而·是将前一个矩阵的行向量与后一个矩阵的列向量相乘。因此·对矩阵的维度有要求,且不满足交换律。相比*,·乘在机器学习中用的更多,ndarray提供了dot()函数来计算·乘。
let arr11: Array2<f64> = arr9.dot(&identity);
println!("{}", arr11);
这次输出就跟我们的预期一致了:
[[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]
同样的道理,我们可以声明3维度或更高维度的数组。例如:
let arr12 = Array::<i8, _>::ones((2, 3, 2, 2));
println!("MULTIDIMENSIONAL\n{}", arr12);
输出的是一个 2 × 3 × 2 × 2 2 \times 3 \times 2 \times 2 2×3×2×2数组
MULTIDIMENSIONAL
[[[[1, 1],
[1, 1]],
[[1, 1],
[1, 1]],
[[1, 1],
[1, 1]]],
[[[1, 1],
[1, 1]],
[[1, 1],
[1, 1]],
[[1, 1],
[1, 1]]]]
用ndarray-rand生成随机数
ndarray-rand提供了比rand更强大的随机功能,且能更好得跟ndarray配合。
要想在交互编程环境中引入ndarray-rand,需要加入如下代码:
:dep ndarray-rand={version = "0.14.0"}
use ndarray_rand::{RandomExt, SamplingStrategy};
use ndarray_rand::rand_distr::Uniform;
下面我们生成一个大小为 2 × 5 2 \times 5 2×5的在满足[1, 10]之间正态分布的矩阵。
let arr13 = Array::random((2, 5), Uniform::new(0., 10.));
println!("{:5.2}", arr13);
输出结果为:
[[ 1.64, 8.13, 5.92, 5.88, 0.45],
[ 7.13, 5.79, 8.21, 4.64, 6.04]]
上面的代码每次运行输出结果都不同,因为每次都是随机生成的,但生成的随机数一定满足[1, 10]之间的正态分布。
我们还可以实现类似Python中random.choice()的功能,随机从数组中选取元素
let arr14 = array![1., 2., 3., 4., 5., 6.];
let arr15 = arr14.sample_axis(Axis(0), 2, SamplingStrategy::WithoutReplacement);
println!("Sampling from:\t{}\nTwo elements:\t{}", arr14, arr15);
输出结果为:
Sampling from: [1, 2, 3, 4, 5, 6]
Two elements: [1, 3]
接下来给大家演示另一种随机采样方法,这种方法需要用到rand包。
首先我们引入需要用到的模块
use ndarray_rand::rand as rand;
use rand::seq::IteratorRandom;
这里我们将ndarray-rand包中的rand重命名为rand。
然后我们就可以仿照rand文档中的示例,用ndarray-rand实现相同的功能
let mut rng = rand::thread_rng();
let faces = "😀😎😐😕😠😢";
let arr16 = Array::from_shape_vec((2, 2), faces.chars().choose_multiple(&mut rng, 4)).unwrap();
println!("Sampling from:\t{}", faces);
println!("Elements:\n{}", arr16);
上面的代码,我们首先创建了一个thread_rng实例,然后创建一个字符串保存一组emoji字符,接下来的代码将从这个字符串中随机选取4个字符,组成一个大小为
2
×
2
2 \times 2
2×2的矩阵。这里随机选取用到了IteratorRandom中的choose_multiple方法,随机从字符串中选择4个字符。
这里注意,choose_multiple的采样数量不能超过字符串中的字符数,否则会报panic。
另外,Array::from_shape_vec返回的是Result类型,表示能否创建给定大小的数组。我们上面的代码简单的unwrap()一下获取Result中的结果。
最终输出结果为:
Sampling from: 😀😎😐😕😠😢
Elements:
[[😠, 😢],
[😐, 😕]]
用ndarray-stats实现统计
接下来我们看一下ndarray-stats,同时介绍一个经常与ndarray-stats配合使用的包noisy_float。
我们将利用ndarray-stats 来验证一下 ndarray-rand生成的正态分布是否真的是正态分布。
首先,我们生成一个大小为 10000 × 2 10000 \times 2 10000×2的矩阵,矩阵中的元素值满足标准正态分布。
use ndarray_rand::rand_distr::{Uniform, StandardNormal};
let arr17 = Array::<f64, _>::random_using((10000,2), StandardNormal, &mut rand::thread_rng());
接下来,我们引入需要用到的统计模块。首先将ndarray-stats和noisy_float引入交互式编程环境:
:dep ndarray-stats = {version="0.5.1"}
:dep noisy_float = {version="0.2.0"}
然后引入如下模块:
use ndarray_stats::HistogramExt;
use ndarray_stats::histogram::{strategies::Sqrt, GridBuilder};
use noisy_float::types::{N64, n64};
接着我们需要将数组中的元素从float转为noisy float。这里我不过多的解释noisy float,你可以简单的将noisy float理解为就是一个float,但是当赋与其非法值时(如NaN)就会报panic。由于noisy float不存在非法值,所以它是安全可排序的,这是ndarray-stats创建直方图等操作必要的条件。noisy float的具体介绍请参考noisy_float文档。
要对ndarray中每一个元素进行操作,我们可以用mapv()。mapv()跟map()类似,传入一个闭包对每一个迭代值机型操作。
let data = arr17.mapv(|e| n64(e));
将数组中的元素转成noisy float后,我们就可以创建统计直方图了。直方图需要以一定的步长切分数据,在ndarray-stats中称之为grid。ndarray-stats提供了GridBuilder来完成数据切分工作。这里我们使用strategies::Sqrt(很多应用都采用此策略,例如我们熟悉的Excel)来帮我们自动推断最佳的切分步长。
let grid = GridBuilder::<Sqrt<N64>>::from_array(&data).unwrap().build();
有了切分步长后我们就可以将其应用到原始数据中得到直方图数据
let histogram = data.histogram(grid);
我们关注的是每个区间内元素的数量,所以我们可以用counts()方法来统计数量
let histogram_matrix = histogram.counts();
这里得到的histogram_matrix 是一个计数矩阵,统计了每个grid内元素的数量。我们的直方图一般是按列统计的,所以我们需要将histogram_matrix按有轴累加起来,这样得到的一维数组就是直方图的统计计数了。
let data = histogram_matrix.sum_axis(Axis(0));
println!("{}", data);
输出结果为:
[2, 0, 1, 0, 5, 5, 1, 4, 9, 2, 4, 12, 8, 13, 17, 11, 20, 32, 32, 30, 32, 43, 47, 66, 65, 89, 110, 114, 110, 131, 147, 170, 173, 194, 209, 206, 255, 259, 264, 280, 292, 255, 288, 294, 335, 300, 306, 324, 287, 323, 275, 280, 284, 250, 244, 247, 192, 230, 178, 191, 162, 147, 150, 128, 110, 99, 83, 93, 83, 68, 47, 50, 30, 32, 34, 21, 24, 13, 14, 15, 9, 12, 4, 4, 7, 2, 3, 1, 0, 1, 1, 1, 0, 0, 3, 0, 0, 0, 0, 2, 0]
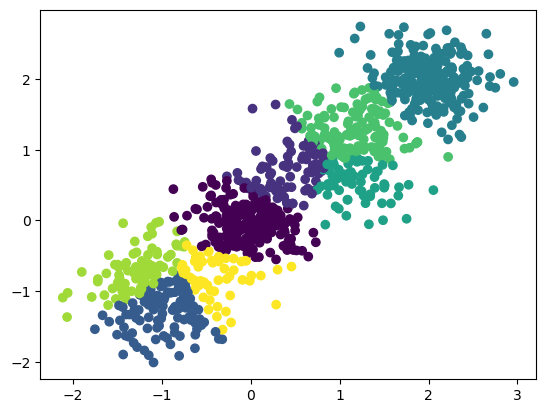
虽然输出结果不如图像直观,但也能感觉到确实是服从正态分布的。为了让大家直观看到结果,我们来将数据可视化。数据可视化是数据分析和机器学习中非常重要的一块,后面我会专门一张讲解如何在交互环境下用plotters进行数据可视化。在这里主要让大家可视化地看一下结果。
:dep plotters = {version="0.3.4", default_features = false, features = ["evcxr", "all_series", "all_elements"]}
extern crate plotters;
use plotters::prelude::*;
let figure = evcxr_figure((640, 480), |root| {
root.fill(&WHITE);
let histogram_matrix = histogram.counts();
let data = histogram_matrix.sum_axis(Axis(0));
let mut chart = ChartBuilder::on(&root)
.set_label_area_size(LabelAreaPosition::Left, 40)
.set_label_area_size(LabelAreaPosition::Bottom, 40)
.caption("随机数分布图", ("sans-serif", 30))
.build_cartesian_2d((0..data.len()).into_segmented(), 0..300)
.unwrap();
chart
.configure_mesh()
.disable_x_mesh()
.bold_line_style(&WHITE.mix(0.3))
.axis_desc_style(("sans-serif", 15))
.draw()?;
chart.draw_series((0..).zip(data.iter()).map(|(x, y)| {
let x0 = SegmentValue::Exact(x);
let x1 = SegmentValue::Exact(x + 1);
let mut bar = Rectangle::new([(x0, 0), (x1, (*y) as i32)], RED.filled());
bar.set_margin(0, 0, 1, 1);
bar
}))?;
Ok(())
});
figure
上面代码会将data中的数据以柱状图的形式显示。

结论
本章我们学习了如何使用ndarray以及它与自带数组和vec的区别。我们还学习了ndarray生态中随机和统计相关的包,这些包一定程度上提供了scipy的相关功能。
其实ndarray的功能远远不止这些,基本上numpy有的功能ndarray都有对应的实现。这篇文章详细对比了ndarray 和 numpy的函数功能,熟悉numpy的同学可以对比着学ndarray,效率会非常高。后面我也会专门做一篇numpy和ndarray方法的详细对比。