数据挖掘（六）层次聚类

1.层次聚类简介

层次聚类算法(Hierarchical Clustering)将数据集划分为一层一层的clusters，后面一层生成的clusters基于前面一层的结果。层次聚类算法一般分为两类：

Divisive 层次聚类：又称自顶向下（top-down）的层次聚类，最开始所有的对象均属于一个cluster，每次按一定的准则将某个cluster 划分为多个cluster，如此往复，直至每个对象均是一个cluster。
Agglomerative 层次聚类：又称自底向上（bottom-up）的层次聚类，每一个对象最开始都是一个cluster，每次按一定的准则将最相近的两个cluster合并生成一个新的cluster，如此往复，直至最终所有的对象都属于一个cluster。

下图直观的给出了层次聚类的思想以及以上两种聚类策略的异同：

;

层次聚类算法是一种贪心算法（greedy algorithm），因其每一次合并或划分都是基于某种局部最优的选择。

2. 自顶向下的层次聚类算法(Divisive)

2.1 Hierarchical K-means算法

Hierarchical K-means算法是“自顶向下”的层次聚类算法，用到了基于划分的聚类算法那K-means，算法思路如下：

首先，把原始数据集放到一个簇C，这个簇形成了层次结构的最顶层
使用K-means算法把簇C划分成指定的K个子簇，形成一个新的层
对于步骤2所生成的K个簇，递归使用K-means算法划分成更小的子簇，直到每个簇不能再划分（只包含一个数据对象）或者满足设定的终止条件。

如下图，展示了一组数据进行了二次K-means算法的过程：

;

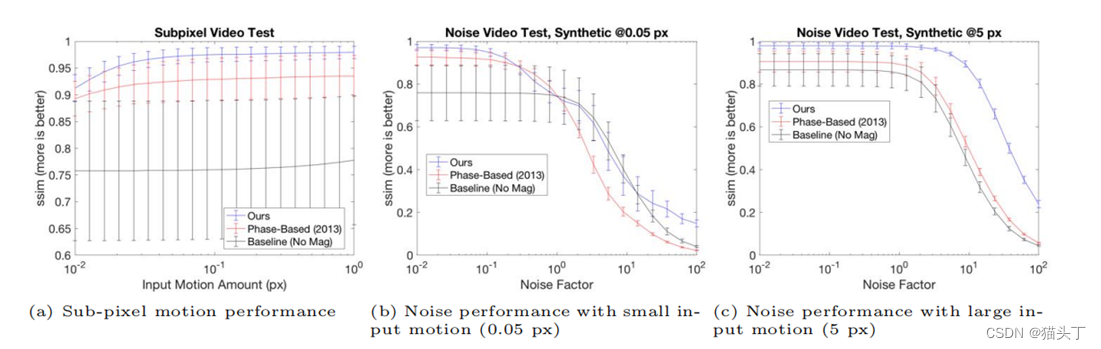
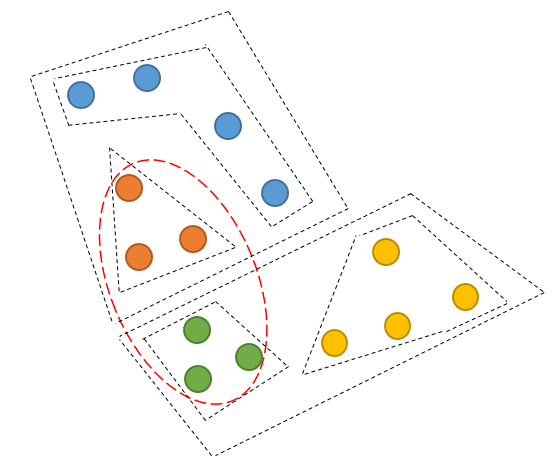
Hierarchical K-means算法一个很大的问题是，一旦两个点在最开始被划分到了不同的簇，即使这两个点距离很近，在后面的过程中也不会被聚类到一起。

;

对于以上的例子，红色椭圆框中的对象聚类成一个簇可能是更优的聚类结果，但是由于橙色对象和绿色对象在第一次K-means就被划分到不同的簇，之后也不再可能被聚类到同一个簇。

Bisecting k-means聚类算法，即二分k均值算法，是分层聚类（Hierarchical clustering）的一种。更多关于二分k均值法，可以查看聚类算法之K-Means。

3. 自底向上的层次聚类算法(Agglomerative)

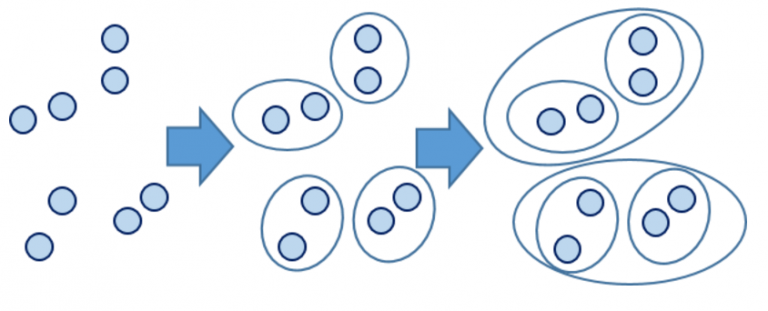
层次聚类的合并算法通过计算两类数据点间的相似性，对所有数据点中最为相似的两个数据点进行组合，并反复迭代这一过程。简单的说层次聚类的合并算法是通过计算每一个类别的数据点与所有数据点之间的距离来确定它们之间的相似性，距离越小，相似度越高。并将距离最近的两个数据点或类别进行组合，生成聚类树。

;

相比于Hierarchical K-means算法存在的问题，Agglomerative Clustering算法能够保证距离近的对象能够被聚类到一个簇中，该算法采用的“自底向上”聚类的思路。

3.1 Agglomerative算法示例

对于如下数据：

;

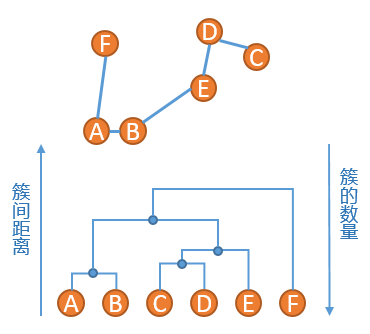
1、将A到F六个点，分别生成6个簇 2、找到当前簇中距离最短的两个点，这里我们使用单连锁的方式来计算距离，发现A点和B点距离最短，将A和B组成一个新的簇，此时簇列表中包含五个簇，分别是{A，B}，{C}，{D}，{E}，{F}，如下图所示：

;

3、重复步骤2、发现{C}和{D}的距离最短，连接之，然后是簇{C,D}和簇{E}距离最短，依次类推，直到最后只剩下一个簇，得到如下所示的示意图：

;

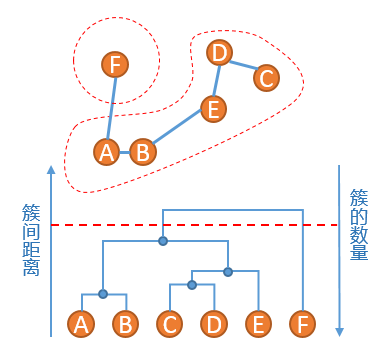
4、此时原始数据的聚类关系是按照层次来组织的，选取一个簇间距离的阈值，可以得到一个聚类结果，比如在如下红色虚线的阈值下，数据被划分为两个簇：簇{A，B，C，D，E}和簇{F}

;

Agglomerative聚类算法的优点是能够根据需要在不同的尺度上展示对应的聚类结果，缺点同Hierarchical K-means算法一样，一旦两个距离相近的点被划分到不同的簇，之后也不再可能被聚类到同一个簇，即无法撤销先前步骤的工作。另外，Agglomerative性能较低，并且因为聚类层次信息需要存储在内存中，内存消耗大，不适用于大量级的数据聚类。

3.2 对象之间的距离衡量

衡量两个对象之间的距离的方式有多种，对于数值类型（Numerical）的数据，常用的距离衡量准则有 Euclidean 距离、Manhattan 距离、Chebyshev 距离、Minkowski 距离等等。

3.3 Cluster 之间的距离衡量

除了需要衡量对象之间的距离之外，层次聚类算法还需要衡量cluster之间的距离，常见的cluster之间的衡量方法有 Single-link 方法、Complete-link 方法、UPGMA（Unweighted Pair Group Method using arithmetic Averages）方法、WPGMA（Weighted Pair Group Method using arithmetic Averages）方法、Centroid 方法（又称 UPGMC，Unweighted Pair Group Method using Centroids）、Median 方法（又称 WPGMC，weighted Pair Group Method using Centroids）、Ward 方法。前面四种方法是基于图的，因为在这些方法里面，cluster是由样本点或一些子cluster（这些样本点或子cluster之间的距离关系被记录下来，可认为是图的连通边）所表示的；后三种方法是基于几何方法的（因而其对象间的距离计算方式一般选用 Euclidean 距离），因为它们都是用一个中心点来代表一个cluster。

假设Ci和Cj为两个cluster，则前四种方法定义的Ci和Cj之间的距离如下表所示：

;

简单的理解：

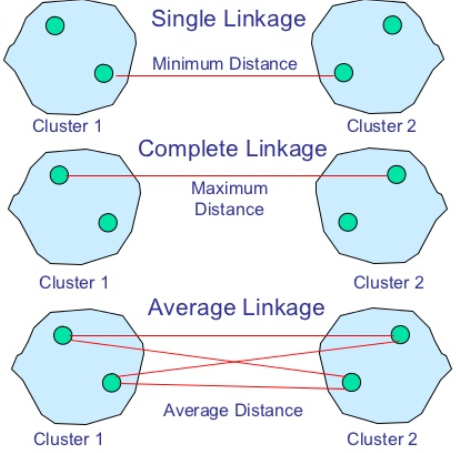
Single Linkage：方法是将两个组合数据点中距离最近的两个数据点间的距离作为这两个组合数据点的距离。这种方法容易受到极端值的影响。两个很相似的组合数据点可能由于其中的某个极端的数据点距离较近而组合在一起。
Complete Linkage：Complete Linkage的计算方法与Single Linkage相反，将两个组合数据点中距离最远的两个数据点间的距离作为这两个组合数据点的距离。Complete Linkage的问题也与Single Linkage相反，两个不相似的组合数据点可能由于其中的极端值距离较远而无法组合在一起。
Average Linkage：Average Linkage的计算方法是计算两个组合数据点中的每个数据点与其他所有数据点的距离。将所有距离的均值作为两个组合数据点间的距离。这种方法计算量比较大，但结果比前两种方法更合理。

;

其中 Single-link 定义两个 cluster 之间的距离为两个 cluster 之间距离最近的两个对象间的距离，这样在聚类的过程中就可能出现链式效应，即有可能聚出长条形状的 cluster；而 Complete-link 则定义两个 cluster 之间的距离为两个 cluster 之间距离最远的两个对象间的距离，这样虽然避免了链式效应，但其对异常样本点（不符合数据集的整体分布的噪声点）却非常敏感，容易产生不合理的聚类；UPGMA 正好是 Single-link 和 Complete-link 的一个折中，其定义两个 cluster 之间的距离为两个 cluster 之间两个对象间的距离的平均值；而 WPGMA 则计算的是两个 cluster 之间两个对象之间的距离的加权平均值，加权的目的是为了使两个 cluster 对距离的计算的影响在同一层次上，而不受 cluster 大小的影响（其计算方法这里没有给出，因为在运行层次聚类算法时，我们并不会直接通过样本点之间的距离之间计算两个 cluster 之间的距离，而是通过已有的 cluster 之间的距离来计算合并后的新的 cluster 和剩余cluster 之间的距离，这种计算方法将由下一部分中的 Lance-Williams 方法给出）。

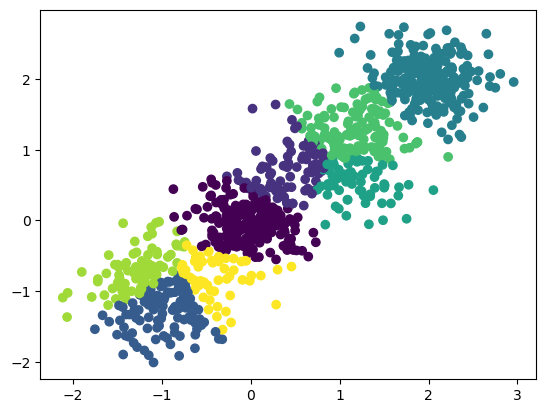
4.实验：BIRCH算法聚类

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import Birch
# X为样本特征，Y为样本簇类别，共1000个样本，每个样本2个特征，共4个簇，簇中心在[-1,-1], [0,0],[1,1], [2,2]
X, y = make_blobs(n_samples=1000, n_features=2, 
                  centers=[[-1,-1], [0,0], [1,1], [2,2]],
                  cluster_std=[0.4, 0.3, 0.4, 0.3],
                  random_state =9)
plt.scatter(X[:, 0], X[:, 1])

在这里插入图片描述

birch = Birch(n_clusters = None)#设置birch函数,n_clusters取值分别为None和4
y_pred = birch.fit_predict(X)##训练数据
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()