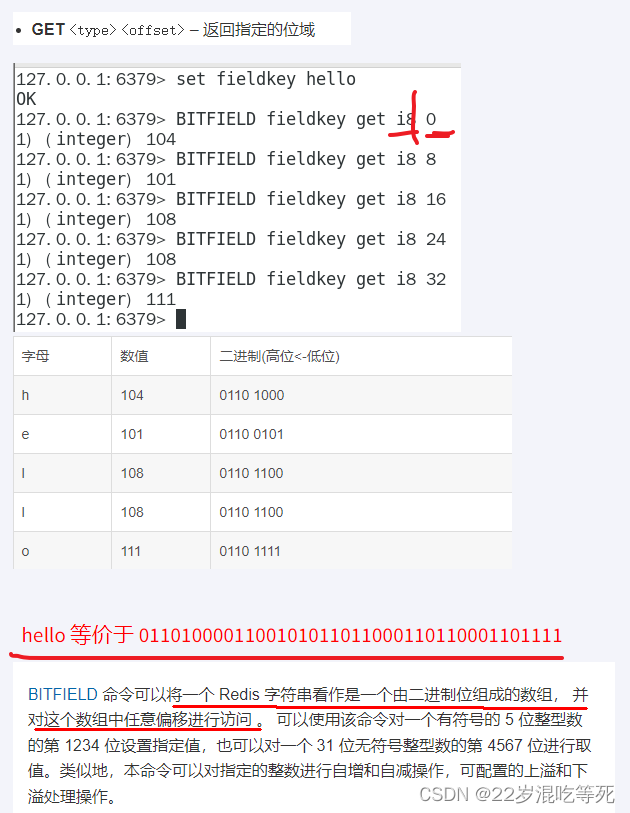
一列数到中位数的总距离最小

- 3554.二进制（二进制数的加减法-转化为十进制运算再将结果转回二进制
- 3565.完美矩阵
- 1824.钻石收藏家（经典双指针）

3554.二进制（二进制数的加减法-转化为十进制运算再将结果转回二进制

输入样例：

2
00000000000000000000000000000000
00000000000000000000000000000001

输出样例：

00000000000000000000000000000001
00000000000000000000000000000011
00000000000000000000000000000010
00000000000000000000000000000100

二进制数进行计算并且输出结果，当然是转化为十进制直接运算再将结果转化为二进制数，脑子秀逗了才会去在二进制的世界按照二进制的规矩一位一位地相加

#include <bits/stdc++.h>
using namespace std;
#define int long long int
int n,T,k;
//void fun(string str){// str + 011
//	string res="";
//	for(int i=str.size()-1;i>=0;i--){
//		if
//	}
//}
void fun(int num){// 123
	for(int i=32;i>=0;i--){
		if((num>>i)&1)cout<<"1";
		else if(i!=32)cout<<"0";//超过 32位的不用补前导 0
	}
	cout<<endl;
}
signed main(){
    cin>>T;
    string str;
    while(T--){
        cin>>str;
        int n=str.size();
       
        int num=0;
        for(int i=0;i<n;i++){
        	num=num*2+str[i]-'0';
		}
		fun(num+1);
		fun(num+3);
    }
    
    return 0;
}

3565.完美矩阵

输入样例：

输出样例：

8
42

样例解释
第一组数据可以通过 8
步操作得到以下矩阵：

第二组数据可以通过 42
步操作得到以下矩阵：

5 6 6 5
6 6 6 6
5 6 6 5

多个村庄分布在一排不同的位置，要在某个村庄设置一个邮局使得所有村庄到达这一个邮局的总距离最小，邮局应该设置在村庄坐标的中位数位置处（同一个坐标可能有多个村庄）
这里相似，一列数，不一定各不相同，要使得所有数相等的操作数最少，最后所有数的值应该等于原先中位数的值
参考
这四个数设为a,b,c,d

设平均数是avg 平均数的答案是(下面的不等式是三角绝对值不等式)

|a−avg|+|b−avg|+|c−avg|+|d−avg||a−avg|+|b−avg|+|c−avg|+|d−avg|
=|a+b−2∗avg|+|d+c−2∗avg|>=|a+b−2∗avg|+|d+c−2∗avg|
=|2∗avg−(a+b)|+|d+c−2∗avg|=|2∗avg−(a+b)|+|d+c−2∗avg|
=|d+c−a−b|>=|d+c−a−b|
=d+c−a−b=d+c−a−b
中位数的答案是
|a−b|+|b−b|+|c−b|+|d−b||a−b|+|b−b|+|c−b|+|d−b|
=b−a+c−b+d−b=b−a+c−b+d−b
=d+c−b−a=d+c−b−a
所以中位数的答案小于平均数
中位数更优

原文链接：https://blog.csdn.net/weixin_55296581/article/details/123281429

#include <bits/stdc++.h>
using namespace std;
#define int long long int
#define PII pair<int,int> 
int m,n,T,k;
const int N=105;
int a[N][N];
signed main(){
	cin>>T;
	while(T--){
		cin>>m>>n;
		for(int i=1;i<=m;i++){
			for(int j=1;j<=n;j++){
				cin>>a[i][j];
			}
		}
		int res=0;
		for(int i=1;i<=(m+1)/2;i++){//回文只要考虑前一半就好 123 取2  1234 也是取到2
			for(int j=1;j<=(n+1)/2;j++){
			    set<PII> s;
			    s.insert({i,j});
			    s.insert({i,n-j+1});
			    s.insert({m-i+1,j});
			    s.insert({m-i+1,n-j+1});
				vector<int> v;
				for(auto t:s){
                    v.push_back(a[t.first][t.second]);
                }
				sort(v.begin(),v.end());
				// auto new_end =unique(v.begin(),v.end());
    //             v.erase(new_end,v.end());
                // 不是规避重复的值，而是规矩相同位置的值TT
				for(int k=0;k<v.size();k++){
					res+=abs(v[k]-v[v.size()/2]);
				}
			}
		}
		cout<<res<<endl;
	}
//1 2  3  4
//5 6  7  8
//9 10 11 18
//对于奇数行(列)的最中间一个数，在其所在的行(列) 不需要使得与别的数相等(回文数列最中间的数独美)
//即i和m-i+1相等，例如以上例子，5不需要和所在列的任何数相等，只需要和8相等，二元组
//当此时它的 列(行)数不为1时，要相等的数是二元组，为1那不需要任何数与他相等
//同时我也想，把所有情况都按照四元组的方式计算，不管i和m-i+1相等与否，统统加上
//反正最终总是求中位数 不管是5 8，还是5 5 8，还是5 8 8 8，要使得所有数相等的操作数总是变为中位数
//实际情况只会出现四元组，二元组，一元组的情况，但不是找中位数有错，
//而是会累计不需要的步骤，比如只有5 8两个数需要相等，按照四元组5 5 8 8，会多算一次(8-5)
//要注意不是规避重复的值，而是规矩相同位置的值TT

    return 0;
}

1824.钻石收藏家（经典双指针）

输入样例：

输出样例：

从来不知道，区区一个减法可以做得这么扭曲，相减就好啦！干嘛要求差分的累加啊
还有枚举的直接就是右端点了，没必要为r赋值

#include <bits/stdc++.h>
using namespace std;
int n,T,k;
 const int N=1e3+5;
 int a[N];
string str;
int d[N];
signed main(){
    
    cin>>n>>k;
    for(int i=1;i<=n;i++)cin>>a[i];
    sort(a+1,a+n+1);
    for(int i=1;i<=n;i++)d[i]=a[i+1]-a[i];
    int res=0;
    int sum=0;//这一段的差分和
    int l=1,r=1;
    for(int i=1;i<=n;i++){
        sum+=d[i-1];
    	while(sum>k){//a[i]-a[l]>k
			sum-=d[l];
			l++;
			
		} 
//     	if(sum<=k){
//          r=i;
//     		res=max(res,i-l+1);
// 		}
		res=max(res,i-l+1);
	}
	cout<<res;
// 1 1 3 4 6
// k=3
    return 0;
}

#include <bits/stdc++.h>
using namespace std;
int n,T,k;
 const int N=1e3+5;
 int a[N];
signed main(){   
    cin>>n>>k;
    for(int i=1;i<=n;i++)cin>>a[i];
    sort(a+1,a+n+1);
    int res=0;
    int l=1,r=1;
    for(int i=1;i<=n;i++){
    	while(a[i]-a[l]>k){
			l++;		
		} 
		res=max(res,i-l+1);
	}
	cout<<res;
// 1 1 3 4 6
// k=3
    return 0;
}