区间预测 | MATLAB实现QRDNN深度神经网络分位数回归时间序列区间预测

效果一览

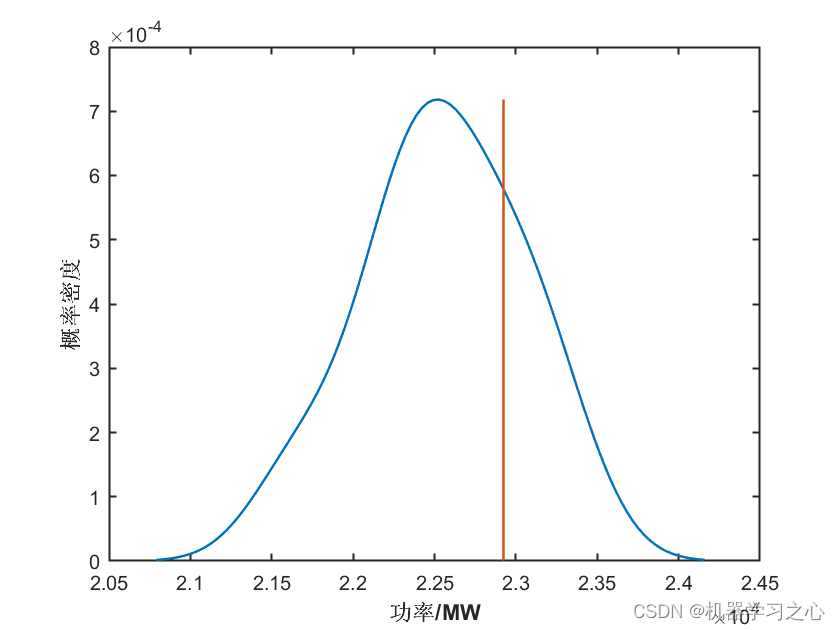
基本介绍

MATLAB实现QRDNN深度神经网络分位数回归时间序列区间预测。QRDNN模型是一种用于时间序列预测的深度神经网络模型，它通过结合深度神经网络和分位数回归的方法，可以实现对时间序列区间预测的能力，具有一定的优势和应用前景

模型描述

• QRDNN（Quantile Regression Deep Neural Network）是一种用于时间序列预测的深度神经网络模型。它通过结合深度神经网络和分位数回归的方法，实现对时间序列区间预测的能力。

• 在QRDNN模型中，首先使用卷积神经网络（CNN）或循环神经网络（RNN）等方法对时间序列数据进行特征提取和表示学习。然后，将提取出的特征输入到分位数回归层中，通过多个分位数输出来实现对不同置信水平的区间预测。

• 具体来说，QRDNN模型可以表示为以下数学公式：

$$y_{\tau }=f_{\tau }(x;\theta )$$

• 其中，$y_{\tau }$表示在置信水平为$\tau$时的预测值，$x$表示输入的时间序列数据，$\theta$表示模型参数。$f_{\tau }$是分位数回归层，它可以通过训练得到。

• QRDNN模型的优点在于，它可以提供对不同置信水平的区间预测，因此可以更好地反映预测结果的不确定性。此外，由于使用了深度神经网络进行特征提取和表示学习，QRDNN模型可以更好地处理复杂的时间序列数据。

程序设计

• 完整程序和数据获取方式：私信博主。

1.Matlab实现基于QRDNN分位数回归深度神经网络的时间序列区间预测模型；
2.多图输出、多指标输出(MAE、RMSE、MSE、R2)，多输入单输出，含不同置信区间图、概率密度图；
3.data为数据集，功率数据集，用过去一段时间的变量，预测目标，目标为最后一列，也可适用于负荷预测、风速预测；MainQRDNNTS为主程序，其余为函数文件，无需运行

%% DNN网络训练
tic
DNNnet = trainNetwork(inputn_train,outputn_train,layers,opts);
toc;
analyzeNetwork(layers)
%% DNN测试数据
function [DNN, state] = TrainRecovery(n)
%% 恢复之前的结果，接着进行训练；或者加载现有神经网络.
% n:各层神经元个数，其中按顺序第一个元素为输入层神经元的个数,
% 最后一个元素为输出层神经元的个数，其余元素为隐藏层的神经元个数.
% DNN: cell数组，依次存放A1, A2, A3, ...和 E, Loss.
% state: 若返回值>0则表示DNN已训练完毕,返回精度.


DNN = LoadNN();

if isempty(DNN)
    % 从头开始训练.
    h = length(n); % 网络层数
    DNN = cell(1, h+1);
    for i = 1:h-1
        % 第一列为偏置项.
        DNN{i} = rand(n(i+1), n(i) + 1) - 0.5;
    end
    % 倒数第2个元素为零列和单位阵的组合.
    DNN{h} = [zeros(n(h), 1), eye(n(h))];
end

disp('DNN infomation:'); disp(DNN);

for i = 1:length(n)
    fprintf('第[%g]层神经元个数: %g.\n', i, n(i));
end

%% 检测此神经网络是否已训练完成.
state = 0;
if isempty(DNN{end})
    return
end
EarlyStopping = 3; %DNN早停条件
loss = DNN{end}(3, 1:end-EarlyStopping);
best = max(loss);
count = 0;
for i = max(length(loss)+1, 1):length(DNN{end})
    if 0 <= DNN{end}(3,i) && DNN{end}(3,i) <= best
        count = count + 1;
        if count == EarlyStopping
            state = best;
        end
    else
        break
    end
end

end
————————————————
版权声明：本文为CSDN博主「机器学习之心」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/kjm13182345320/article/details/129066749

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/127931217
[2] https://blog.csdn.net/kjm13182345320/article/details/127418340
[3] https://blog.csdn.net/kjm13182345320/article/details/127380096