1 进入情境

生日，朋友送了一堆弹珠，有大有小；我想找出自己的幸运数字8对应的那颗弹珠。有什么办法呢？

排序，然后从头数到第八个。
找八次，每次找到最小的后，放到一边。

比较一下哪个好？

排序很烦，因为朋友送了我一卡车弹珠，而我只想要第八个，工作量太大，不实际。
找八次，每次都要从一车里找最小的，也很累。好在朋友附赠了一个魔法道具——金字塔。

1-1 金字塔道具

就是把一车弹珠从金字塔的头上倒入，按下开关，最小的弹珠就被放到金字塔的塔尖了。这样反复取走头顶的最小弹珠、再按，八次之后就能拿到幸运弹珠了！
金字塔还有其他的俗名，像小顶堆、隐式二叉堆、斐波那契堆和其他堆，效果是一样的。
效率 O(KlgN)

1-2 感觉还不够

取了八次，得到的是前八个有序的弹珠，但前七个我都不想要，能不能一步到位，直接跳过前面步骤，直接找出我要的第八颗弹珠呢？
比如，更加NB的魔法道具？
就是你啦，妙蛙种子！……不好意思串台了。闪烁着金色光芒的传说中的厨具——万能筛子！！！

1-3 万能筛子

正经的筛子是一种带孔的网，大于孔的会被留住筛子里，小于孔的会掉下去。如上所示，孔的大小是固定的。
神奇筛子就厉害了，允许控制孔的大小。试想，假如凭直觉估到了第八颗弹珠的大小，设为孔径，只需把一车弹珠往筛子上这么哗哗一倒，筛出十来颗弹珠，岂不是爽歪歪。可能眼睛一扫就出结果，这多快！

1-4 怎么用呢

为了方便说清楚，假设我们要找第K颗弹珠，默认是从小到大的次序。

随机选一颗弹珠pivot作为孔洞的大小，筛一筛，之后得到两部分，筛子里剩下大A颗，筛子外出现小b颗。
看幸运弹珠在哪一堆里，若K< 小b，说明幸运弹珠就在筛子外的小珠子里，回到第一步继续选第K颗；
若K等于小b，说明说明幸运弹珠就是pivot，找到了！
若K> 小b，说明幸运弹珠还在筛子里，调整孔的大小，继续筛里面的弹珠。注意，因为这次已经找到了前小b颗，所以接下来只需要回到第一步找第(K- 小b)颗弹珠。

性能 O(N)

2 代码实现

2-1 伪代码描述

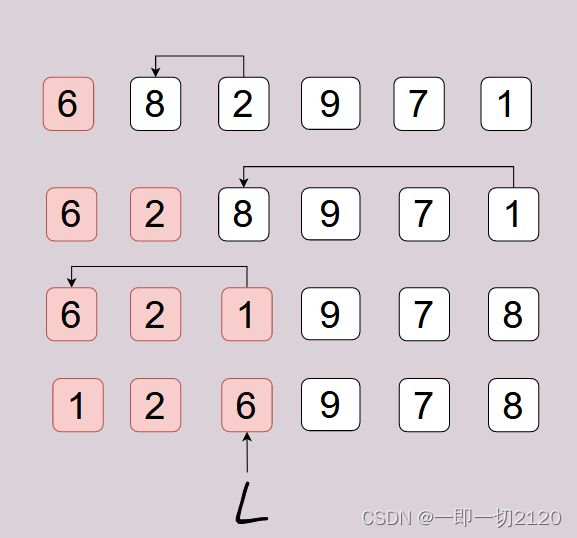
Top(k,A,l,r)表示在数组A[l,r]中查找第k小的数。
Partitio(A,l,r):以首元素A[l]为枢纽pivot，将数组A分为两部分，小于枢纽的放前面，大于枢纽的放后面，结束后返回枢纽的正确下标L=2。如下图所示，A[l,L]是已经满足不大于枢纽的部分。


function Top(k,A,l,r):
	Exchange A[l] <--> A[Random(l,r)] #随机选一个元素作为pivot放到起点位置
	p <- Partition(A,l,r)# 按首元素划分，返回pivot的数组下标p
	nth <- p-l+1 #pivot 在当前范围的数组中是第nth个
	if  nth == k then
		return A[p]
	if k < nth then
		return Top(k,A,l,p-1)
	return Top(k-nth,A,p+1,r)
		
function Partitio(A,l,r):
	pivot <- A[l]
	L <- l
	for R <- l+1 to r do
		if not (pivot < A[R]) then # 发现一个逆序的数
			L<- L+1 # 首个可交换的大于枢纽的值的下标
			Exchange A[L]<-->A[R]
	Exchange A[L]<-->A[l]# 把枢纽值放到分界线上
	return L

2-2 完整实例c++

#include <iostream>
#include <vector>
#include <string>
#include <queue>
#include<cstdlib> //rand() 获取随机数

using namespace std;
#define see(x) cout << x << endl
#define see2(x, y) cout << (x) <<"\t"<< (y) << endl

class Solution
{
    using Array=vector<int> ;
public:
    int topKth(int kth,Array &A,int l,int r){//修改数组要传入引用
        if(l>r) return -1; //检查下标的合法性

        if(l==r&&kth==1) return A[l]; //只有一个数，可能会对0取余
        swap(A[l],A[rand() % (r-l)+l]);
        
        int p=partition(A,l,r);//小堆 枢纽 大堆中枢纽的下标
        int ith=p-l+1;

        if(ith==kth) return A[p];
        if(ith>kth) return topKth(kth,A,l,p-1);//在小堆A[l,p-1]里找
        return topKth(kth-ith,A,p+1,r);//在大的堆A[p+1,r]里找
    }

    int partition(Array &A,int l,int r){
        int pivot=A[l];
        int R,L=l;
        for(R=l+1;R<=r;++R){
            if(!(pivot<A[R])){//!优先级高于<
                swap(A[++L],A[R]);
            }
        }
        swap(A[L],A[l]);//注意复位
        return L;
    }
    


};

void test()
{
    vector<int> A{6,8,2,9,7,1}; 
    vector<int> sortedA{1,2,6,7,8,9};
    
    Solution sol;
    
    //test partition()
    // sol.partition(A,0,5);
    // for(auto& x:A){
    //     see(x);
    // }

    bool pass=true;
    for (size_t ith = 1; ith <= A.size(); ++ith)
    {
        int now=sol.topKth(ith,A,0,5);
        // see2(ith,now);
        if(sortedA[ith-1]!= now)//idx+1=ith
        {
            pass=false;
            break;
        }
    }
    
    if (pass)
    {
        see("Accept!!!");
    }
    else
    {
        see("something error.");
    }
}

int main()
{
    test();
    return 0;
}

3 引申

3-1 完美的折半舍弃

把列表划分为若干小组，每个组最多5个元素；
计算每个组的中间值，得到N/5个数；
继续寻找中值的中值，在O(lgn)时间内得到真正的中值。
以此中值作为枢纽切分,每次都会舍弃一半。

总体效率 T(n)=a*lgn+b*n+T(n/2)，a是求中值的中值的常系数；b是划分的常数系数，如1/5；利用主定理，可得总性能为 O(n)；证明请移步使用主定理求解递归式。

伪代码说明：

function findPivot(A,l,r):
	#出口
	alen <- r-l+1
	if alen <= 5 then
		sort(A,l,r)
		return A[(l+r)/2]
   #切分 获得新数组B
   blen <- alen / 5
   for i=0 to blen-1 do
		now_l <- l+5*i
		now_r <- now_l+4
		if now_r > r then
			now_r <- r
		B[i]<-findPivot(A,now_l,now_r)
	#递归,中值的中值
	return findPivot(B,0,blen)

C++实现

#include <iostream>
#include <vector>
#include <string>
#include <queue>
#include<algorithm>//sort()
#include<cstdlib> //rand() 获取随机数
#include<cmath> //ceil(2.3) 取不小于2.3的下一个整数 

using namespace std;
#define see(x) cout << x << endl
#define see2(x, y) cout << (x) <<"\t"<< (y) << endl

class Solution
{
    using Array=vector<int> ;
public:
    int findPivot(Array &A,int l,int r){
        int na=r-l+1;
        if(na<=5){
            // 也可以对A[l,r]排序，取中值
            // 这里直接暴力求平均，拿和均值最接近的那个
            int pivot=-1;
            int sum=0;
            for(int i=l;i<=r;i++) sum+=A[i];
            double avg=(sum*1.0)/na;
            double det=1e10;
            for(int i=l;i<=r;i++) {
                if(abs(A[i]-avg)<det){
                    det=abs(A[i]-avg);
                    pivot=A[i];
                }
            }
            return pivot;
        }

        int nb=ceil(na/5.0);
        Array B(nb,0);
        for (size_t i = 0; i < nb; i++)
        {
            int L=l+5*i;
            int R=L+4;
            if(R>r) R=r;
            B[i]=findPivot(A,L,R);
        }
        return findPivot(B,0,nb);
        
    }
    
    int topKth(int kth,Array &A,int l,int r){//修改数组要传入引用
        if(l>r) return -1; //检查下标的合法性
        if(l==r&&kth==1) return A[l]; //只有一个数
        
        int p=partition(A,l,r);//小堆 枢纽 大堆中枢纽的下标
        int ith=p-l+1;

        if(ith==kth) return A[p];
        if(ith>kth) return topKth(kth,A,l,p-1);//在小堆A[l,p-1]里找
        return topKth(kth-ith,A,p+1,r);//在大的堆A[p+1,r]里找
    }

    int partition(Array &A,int l,int r){
        int pivot=findPivot(A,l,r);//递归获取中位数
        int L=l,R=r+1;
        int pi=-1;//枢纽记录其下标

        while(L<R){
            while (A[L]<pivot&&(++L)<r);
            while(A[--R]>pivot&&R>L);
            if(L<R){
                swap(A[L],A[R]);
                if(A[L]==pivot) pi=L;
                if(A[R]==pivot) pi=R;
            }
        }
        swap(A[pi],A[L]);
        return L;
    }
    


};

void test()
{
    vector<int> A{6,8,2,9,7,1,3,5,4,10}; 
  
    Solution sol;
    
    // test findPivot
    // see(sol.findPivot(A,0,5));

    // test partition
    // sol.partition(A,0,A.size()-1);
    // for(auto x:A){
    //     see(x);
    // }

    see(sol.topKth(9,A,0,A.size()-1));


}

int main()
{
    test();
    return 0;
}