学习《高性能计算:现代系统与应用实践》(Thomas Sterling,Matthew Anderson,Maciej Brodowicz)第 7 章 OpenMP 的基础
OpenMP
- OpenMP 是一个 API
- C、C++、Fortran
- OpenMP 是共享内存的多线程编程模型
- 共享内存
- 默认所有线程可以直接访问全局变量
- 可以限制变量为各线程私有(e.g. 索引变量
i)
- 线程并行
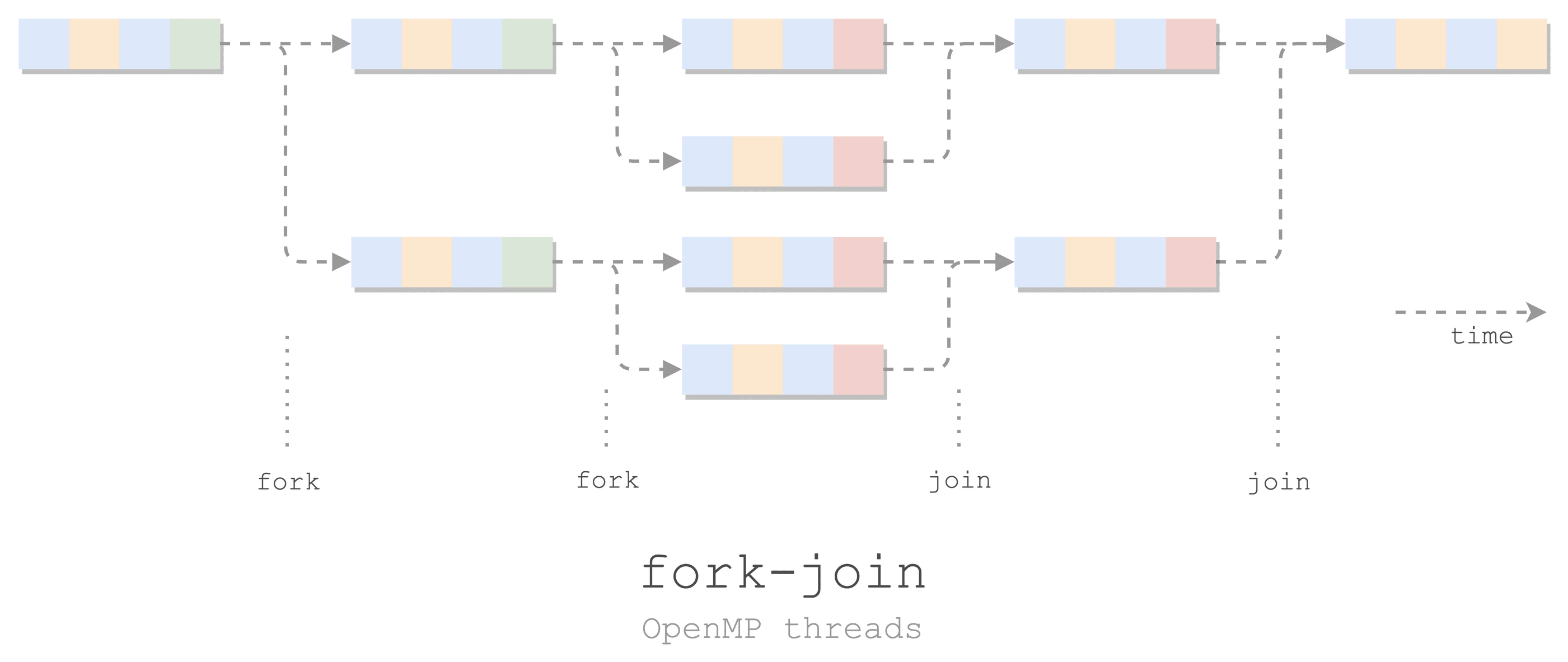
- master/worker 线程:fork-join 模型
- 分支:SPMD(单程序多数据)
- 聚合:隐式栏栅同步:超出当前访问前,所有线程都要完成
- 共享内存
环境变量
export OMP_NUM_THREADS=8 # 开几个线程,默认自动看 CPU
export OMP_DYNAMIC=TRUE # 动态线程数量
export OMP_NESTED=TRUE # 允许嵌套并行
export OMP_SCHEDULE=schedule.chunk # 循环的负载分布
使用 OpenMP
不用安装:
- GCC 内置了 OpenMP 支持!
- 编译的时候带上
-fopenmp就行。
导入:
#include <omp.h>
基本函数:
omp_get_num_threads() // 有多少个并行的进程: OMP_NUM_THREADS
omp_get_thread_num() // 我(当前进程)的 id
// master: 0; worker: [1, OMP_NUM_THREADS)
OpenMP 指令(制导语句):
#pragma omp <directive> <clauses> <statement>
Hello World
// hello.c
#include <omp.h>
#include <stdio.h>
int main() {
#pragma omp parallel
{ // fork
int num_threads = omp_get_num_threads();
int thread_id = omp_get_thread_num();
printf("Hello world from %d (total %d)\n", thread_id, num_threads);
} // join
return 0;
}
魔法是 #pragma omp parallel:串行 -> 并行。派生出 OMP_NUM_THREADS 个进程来并行跑其后的一个代码块。
编译运行:
$ gcc-11 -fopenmp hello.c
$ ./a.out
Hello world from 1 (total 4)
Hello world from 0 (total 4)
Hello world from 3 (total 4)
Hello world from 2 (total 4)
顺序是那种乱七八糟的:并行。觉得不明显可以指定线程数量,再运行:
$ OMP_NUM_THREADS=100 ./a.out
Hello world from 2 (total 100)
Hello world from 11 (total 100)
...
Hello world from 35 (total 100)
...
Hello world from 0 (total 100)
Hello world from 98 (total 100)
私有变量
上面那个程序的另一种版本:
- 预先定义两个变量,但是指定为各线程私有
- 只让 id 为 0 的进程,即主线程获取
num_threads - (其实我试了,编译成汇编和上面那个区别不大,两个变量结束并行之后都不是有效值。
所以目前还不清楚这样在外面先定义好变量有啥优势这个问题大致有答案了,见后文:[[#Why private]]。我还是喜欢局部变量就局部去定义。) ^b5e08c
// hello-v2.c
#include <omp.h>
#include <stdio.h>
int main() {
int num_threads, thread_id;
#pragma omp parallel private(num_threads, thread_id)
{
thread_id = omp_get_thread_num();
printf("Hello world from thread %d.\n", thread_id);
if (thread_id == 0) {
num_threads = omp_get_num_threads();
printf("Total number of thread is: %d\n", num_threads);
}
}
// printf("End of parallel: %d, %d\n", thread_id, num_threads);
// End of parallel: 1, 61694048
return 0;
}
编译运行:
$ gcc-11 -fopenmp hello-v2.c; ./a.out
Hello world from thread 0.
Total number of thread is: 4
Hello world from thread 3.
Hello world from thread 2.
Hello world from thread 1.
小结:OpenMP 并行:
#include <omp.h>
int main() {
#pragma omp parallel
{
并行的代码;
}
}
- 默认各线程共享上下文中的变量:在
omp parallel后面加private(...)指定要各线程私有的变量。
OpenMP 并行
并行 for
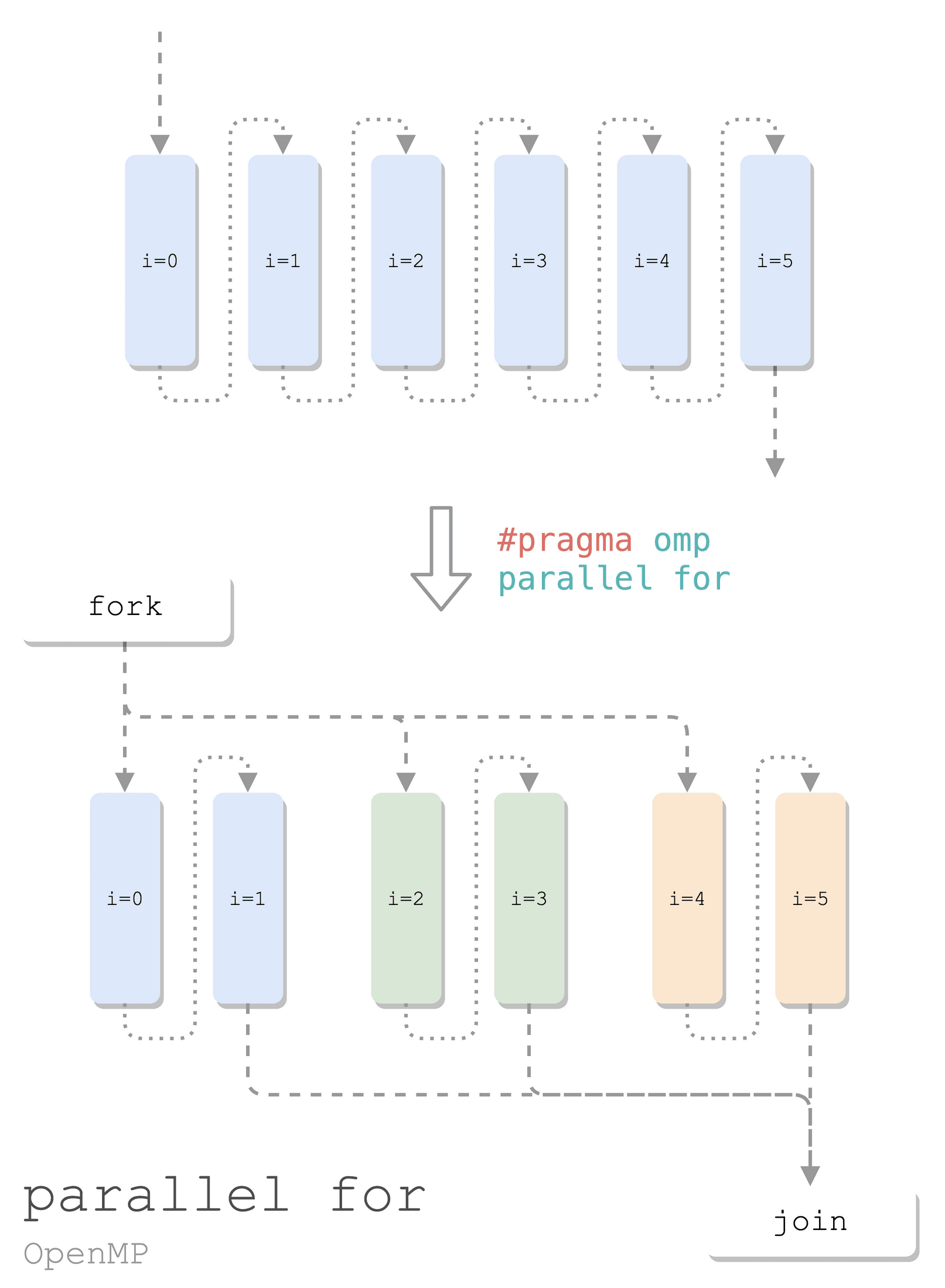
线程间循环分布:通过 OpenMP,让多个线程同时(并行)处理一个 for 循环。
#include <stdio.h>
#include <stdlib.h>
int main() {
const int N = 20;
int num_threads, thread_id;
double a[N], b[N], result[N];
for (int i = 0; i < N; i++) {
a[i] = 1.0 * i;
b[i] = 100.0 * i;
}
for (int i = 0; i < N; i++) {
result[i] = a[i] + b[i];
}
printf("TEST result[19]=%g\n", result[19]);
// TEST result[19]=1919
return 0;
}
要并行化处理合并两个数组的操作,只需加 5 行:
#include <omp.h> // +1
int main() {
...
#pragma omp parallel // +2
{ // +3
#pragma omp for // +4
for (int i = 0; i < N; i++) {
printf("%d: i=%d\n", omp_get_thread_num(), i);
result[i] = a[i] + b[i];
}
} // +5
printf("TEST result[19]=%g\n", result[19]);
return 0;
}
此处的魔法是 #pragma omp for,把 for 分配给各个线程。中间额外加了一个 printf,可以看到 20 次循环,被几个线程平分:
0: i=0 ... 0: i=4
2: i=10 ... 2: i=14
3: i=15 ... 3: i=19
1: i=5 ... 1: i=9
TEST result[19]=1919
如果露掉这一行 #pragma omp for,OpenMP 便无从得知你要并行这个 for。那就比较“精彩”了,4 个线程,把循环各跑一遍,极致反向优化:
0: i=0 ... 0: i=19
1: i=0 ... 1: i=19
2: i=0 ... 2: i=19
3: i=0 ... 3: i=19
TEST result[19]=1919
这个操作太常用了,所以有简化的写法:
#pragma omp parallel for
for (int i = 0; i < N; i++) {
printf("%d: i=%d\n", omp_get_thread_num(), i);
result[i] = a[i] + b[i];
}
小结:并行 for:
#pragma omp parallel
{
#pragma omp for
for (;;) {}
}
⬇️ 复合魔法
#pragma omp parallel for
for (;;) {}
- 可选:
omp for后面加子句schedule(static.chunk),指定切分循环的方式。
并行 sections
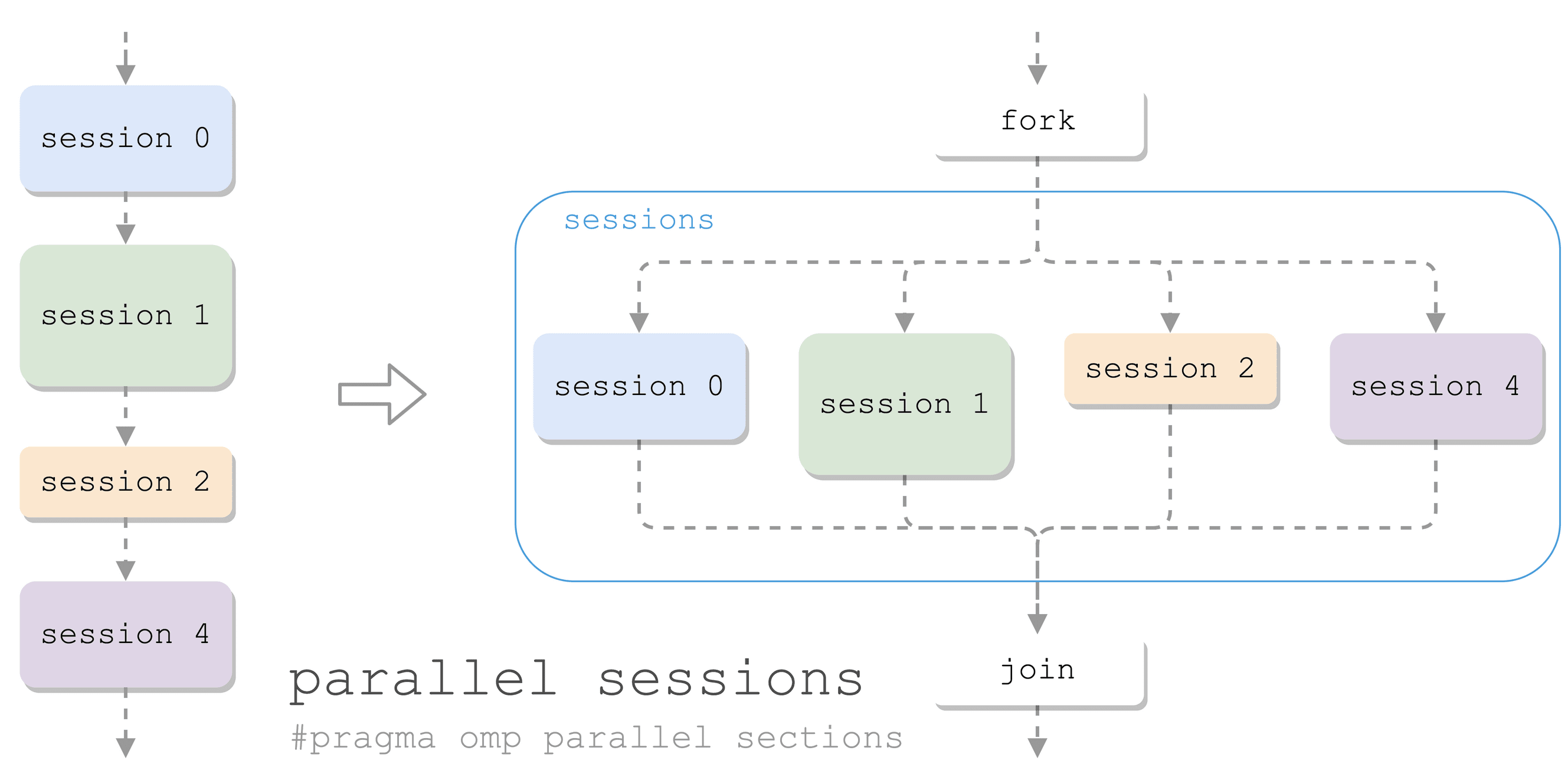
有多块代码要并发执行:
- 一个块称为一个 section
- 多个 section 在一个 sections 中并行
- 一个线程处理一个 section
#pragma omp parallel
{
#pragma omp sections
{
{ /* section 0 */ }
#pragma omp section
{ /* section 1 */ }
#pragma omp section
{ /* section 2 */ }
...
}
}
类似于 parallel for,如果开并行只是为了执行 sections,也可以用合并的 parallel sections:
#pragma omp parallel sections
{
{ /* section 0 */ }
#pragma omp section
{ /* section 1 */ }
...
}
一个例子:并行地对一列数据进行统计,求最值、均值、方差:
#include <omp.h>
#include <stdio.h>
#include <stdlib.h>
int main() {
const int N = (1<<29); // N doubles: 4 GiB
// const int N = 10;
double *x = calloc(N, sizeof(double));
// #pragma omp parallel for // 初始化
for (int i = 0; i < N; i++) {
x[i] = i;
}
// 总和、均值、平方的总和
double sum = 0.0, avg = 0.0, sum2 = 0.0;
#pragma omp parallel sections shared(x, sum, avg, sum2)
{
// section 0: 计算 最大最小值
{
double max = (1<<31), min = (1<<31) - 1;
for (int i = 0; i < N; i++) {
if (x[i] < min) min = x[i];
if (x[i] > max) max = x[i];
}
printf("min: %f\nmax: %f\n", min, max);
}
#pragma omp section // section 1: 计算总和、均值
{
for (int i = 0; i < N; i++) {
sum += x[i];
}
printf("sum: %f\n", sum);
avg = sum / N;
printf("avg: %f\n", avg);
}
#pragma omp section // section 2: 计算平方的均值
{
for (int i = 0; i < N; i++) {
sum2 += x[i] * x[i];
}
printf("sum2: %f\n", sum2);
}
}
// 方差 = 平方的均值 - 均值的平方
double var = sum2 / N - avg * avg;
printf("var: %f\n", var);
return 0;
}
注意这里使用了全局共享的 sum 等几个量,是为了在并行结束后,留下这些值,用于计算方差。
编译运行,对比去掉 parallel 的版本,似乎有一定的提升:
$ openmp gcc-11 -fopenmp sections.c; time ./a.out
min: 0.000000
max: 536870911.000000
sum2: 51580834826121141939077120.000000
sum: 144115187606093856.000000
avg: 268435455.125000
var: 24019198213991840.000000
./a.out 7.34s user 4.00s system 101% cpu 11.200 total
$ openmp gcc-11 -fopenmp no-sections.c; time ./a.out
min: 0.000000
max: 536870911.000000
sum: 144115187606093856.000000
avg: 268435455.125000
sum2: 51580834826121141939077120.000000
var: 24019198213991840.000000
./a.out 8.41s user 9.52s system 72% cpu 24.587 total
OpenMP 同步
共享内存:
- OpenMP 的多个并发线程之间共享全局数据
- 无需 send/recv 的消息传递在并发进程之间交换数值
同步机制:
- 协调并行程序中多个并行线程的执行
- 控制顺序:避免竞争 -> 冲突
- 隐式:join 栅栏
- 显示:critical、master、barrier、single
critical 指令
临界同步指令 critical:多个并行线程互斥访问共享变量。
#paragma omp critical
{ ... }
e.g. 尝试做个并行计数器:
#include <omp.h>
#include <stdio.h>
int main() {
int n = 0;
#pragma omp parallel for shared(n)
for (int i=0; i < 40000; i++) {
#pragma omp critical
n = n + 1;
}
printf("n: %d\n", n);
return 0;
}
编译运行(运行了很多次都是对的):
$ openmp gcc-11 -fopenmp critical.c; time OMP_NUM_THREADS=1000 ./a.out
n: 40000
OMP_NUM_THREADS=1000 ./a.out 0.01s user 0.05s system 16% cpu 0.390 total
如果删掉 #pragma omp critical,就会出现喜闻乐见的错误结果(多运行一些次就能看到各种不同的错误结果):
$ openmp gcc-11 -fopenmp no-critical.c; time OMP_NUM_THREADS=1000 ./a.out
n: 39960
OMP_NUM_THREADS=1000 ./a.out 0.01s user 0.06s system 63% cpu 0.104 total
master 指令
master 指令:只有主线程执行这一块代码,其他线程遇到则跳过。
- 主线程:执行这一块代码
- 其他线程:直接往下走,不等
#pragma omp master
{ ... }
barrier 指令
barrier 指令:同步所有并发线程:
- 遇到 barrier 的线程就停下来,等;
- 等所有进程都到了 barrier 才能继续。
#pragma omp barrier
single 指令
single 指令:宽松版 master + 隐式 barrier:
- 在代码块(
{ ... })后面放一个隐式 barrier; - 允许任意线程 Foo 执行代码块;
- 其他线程跳过代码块执行,但是阻塞在 barrier,等 Foo 酱执行完代码块再放行。
#pragma omp single
{ ... }
reduction 指令
规约:将大量值组合在一起,生成单个结果值。
Reduction:the action or fact of making a specified thing smaller or less in amount, degree, or size
—— New Oxford American Dictionary这里所谓规约就是让值的个数变少的操作。(回想一下 Lisp 就很形象了。)
OpenMP 可以用 reduction 指令做规约:
double result;
#pragma omp reduction(op : result)
{
result = ...; // 局部 result
}
// 全局 result: result = reduce(op, results)
op为某种运算:+,-,*,/,&,|,^中的一个;- 更复杂的规约也容易使用其他同步的方式实现。
result为结果变量,注意这个值在块内是各线程私有,出来之后变成全局的、规约得到的结果。
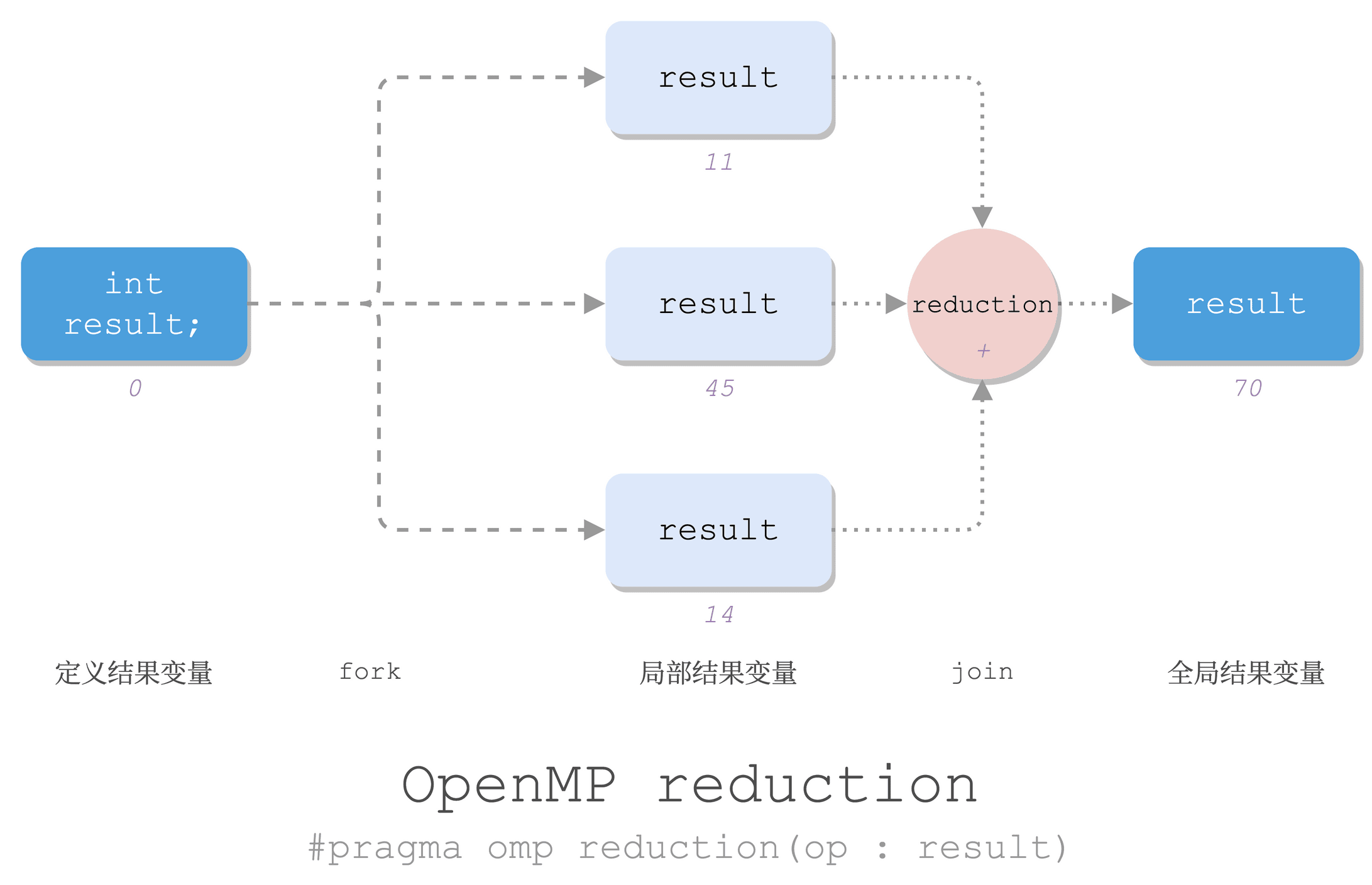
e.g.
#include <stdio.h>
#include <omp.h>
int main() {
const int N = 16;
float a[N], b[N], result;
for (int i = 0; i < N; i++) {
a[i] = i * 1.0;
b[i] = i * 2.0;
}
#pragma omp parallel for reduction(+ : result)
for (int i = 0; i < N; i++) {
result += a[i] * b[i];
}
printf("Result = %f\n", result);
return 0;
}
编译运行:
$ gcc-11 -fopenmp reduction.c; ./a.out
Result = 2480.000000
闲聊
Why pragma
#pragma 是什么鬼啊?pragma 来源于 pragmatic(务实的),,所以关联的点是什么。。
Pragma,也叫做 directive。Directive 就是“指示”的意思,不知到是如何惨遭毒手,被翻译为“制导语句”的。。不翻译成“42 号混凝土”我是不敢苟同的。
总之这东西就是用来指导编译器如何编译的。(教编译器做事)
(对了,我最讨厌这种要左手连打几个字母的词了,顺便吐槽一下“Database”,这个词简直了,尤其是要大写时。其实换一种角度来考虑,还是键盘键位设计的锅。)
Why private
private 子句有何用?[[#^b5e08c|前文]]提到,在各线程内定义局部变量可以完全避免 private,但这是站在一开始就编写 OpenMP 并行代码的角度来设计得到的结果。
OpenMP 设计的一项初衷是在尽可能少改动原有串行代码的基础上,加入并行支持。理想的情况只需加入尽可能少的制导语句(#pragma omp parallel、#pragma omp parallel for 等)就可以让原本串行的代码变并行。
所以就有这种场景:原本的代码如下:
int i, j;
for(i = 0; i < n; i++) {
for(j = 0; j < n; j++) {
//do something
}
}
要使其支持并发,有 private 的支持,只需加一行制导语句,完全不需要改动原有任何一行代码:
int i, j;
#pragma omp parallel for private(j)
for(i = 0; i < n; i++) {
for(j = 0; j < n; j++) {
//do something
}
}
但如果没有 private,就需要改动原有代码结构,把 j 的定义移动到第一层循环内:
int i;
#pragma omp parallel for
for(i = 0; i < n; i++) {
int j;
for(j = 0; j < n; j++) {
//do something
}
}
如果需要为 C89 (所有变量定义要写到 scope 顶部)写的代码加入并行性,这个 private 对于还是比较有意义的。
所以更多是一种兼容性吧。
最近学这些计算(有没有一种可能计算机本来就是用来做计算的😭),还真有好多代码是八几年、九几年写的,有些甚至写的是 K&R C,一直沿用至今,正确、高效、优雅、美观,真的 nb(褒义,由衷赞叹,写的确实漂亮,以带着最深沉偏见的、最批判的锋利目光去看,也无可挑剔)。
再看看现在好多所谓学“*”的 * 写的代码,我没有针对 * 语言,我是说 * 写的任何程序,真的 nb(贬义。那些“代码”,笑死,看别人接手是喜剧,要自己接手是悲剧;眼睁睁看着别人写出这种代码是人间炼狱)。
- StackOverflow: OpenMP: are local variables automatically private?
- StackOverflow: Is there any difference between variables in a private clause and variables defined within a parallel region in OpenMP?
- StackOverflow: Variable declaration placement in C