题目

给定一个由 0 和 1 组成的矩阵 mat ，请输出一个大小相同的矩阵，其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。

两个相邻元素间的距离为 1 。

示例 1：

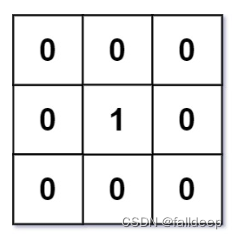
输入：mat = [[0,0,0],[0,1,0],[0,0,0]]
输出：[[0,0,0],[0,1,0],[0,0,0]]
示例 2：

 

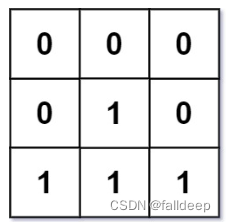
输入：mat = [[0,0,0],[0,1,0],[1,1,1]]
输出：[[0,0,0],[0,1,0],[1,2,1]]
 

提示：

m == mat.length
n == mat[i].length
1 <= m, n <= 104
1 <= m * n <= 104
mat[i][j] is either 0 or 1.
mat 中至少有一个 0 

思路

BFS,跟树的遍历不同，图的遍历刚开始可能有多个节点，我们首先需要将为0的节点插入到队列中，将为1的节点值设置为-1，防止重复查找，然后再遍历整个队列就行

代码

class Solution {
public:
    vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
        queue<pair<int, int>> q;
        int m = mat.size(), n = mat[0].size();
        //遍历一遍mat，队列中插入为0的点，并从这些点开始扩散
        for(int i = 0; i < m; i ++)
            for(int j = 0; j < n; j ++)
            {
                if(mat[i][j] == 0) q.push({i, j});
                else mat[i][j] = -1;//如果是1，都赋初值为-1，代表未查找过，防止重复查找
            }

        while(q.size())
        {
            auto t = q.front();
            q.pop();

            int x = t.first, y = t.second;
            int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
            for(int i = 0; i < 4; i ++)//上下左右
            {
                int a = dx[i] + x, b = dy[i] + y;
                if(a >= 0 && a < m && b >=0 && b < n && mat[a][b] == -1)
                {
                    mat[a][b] = mat[x][y] + 1;
                    q.push({a, b});
                }
            }
        }
        return mat;
    }
};