1.孤立核

        一看到核函数，我们第一时间想到的就是核函数通过升维或者降维的方式来计算数据之间的相似度。他在SVM和聚类算法中应用广泛。

        我们就直入主题来看一下孤核函数的数学推导。

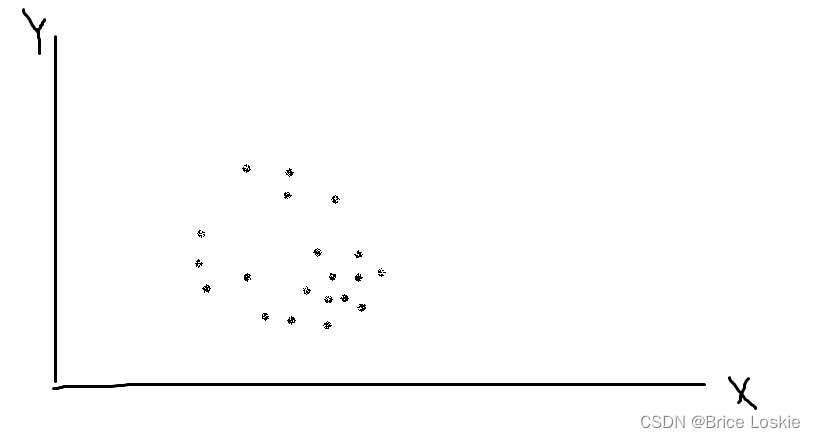
 在d维的空间分布着n个点。数学表达式为.

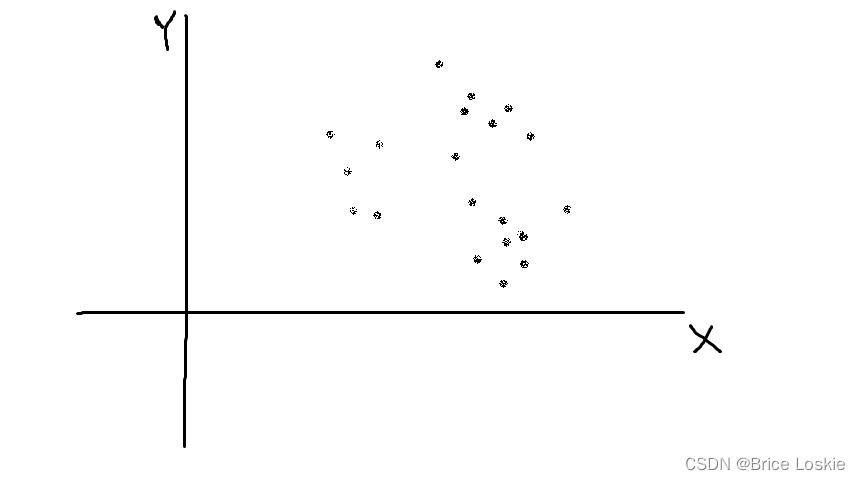
 如图：一共20个点分布在2维空间。即n=10,d=2

表示我们将数据集D划分为个分区分区的所有可行方案。

 ,即H是其中的一种划分。

如下图：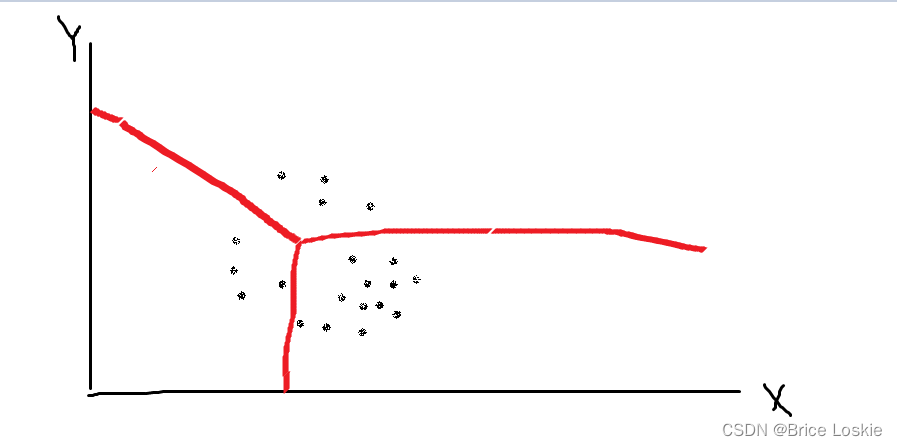

 

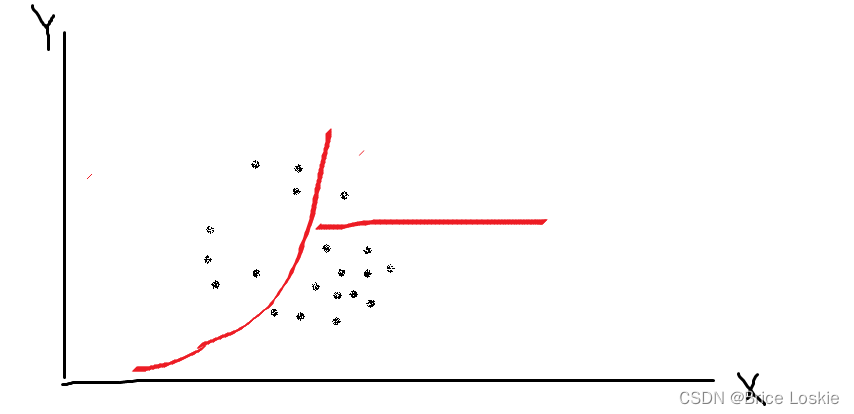
20个点时候会有成百上千个划分方法。

当我们精确到具体的一种划分方法的时候：

其中是具体到的某一种划分区域，如下图所示

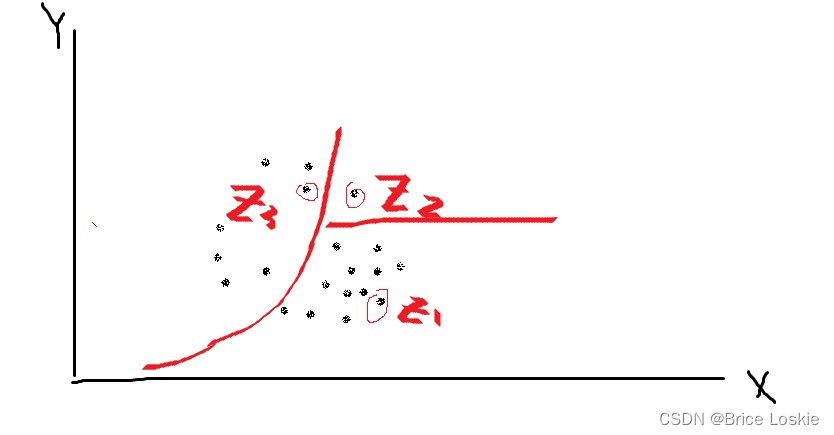
  我们先随机找个点，如上图，我们找3个点。是将和其他-1个点分开的区间划分

 

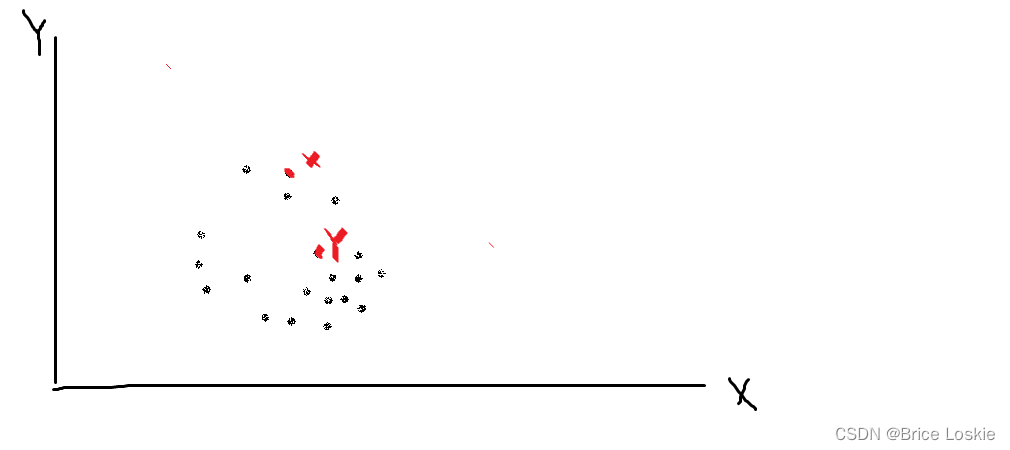
计算两个点的核距离：

我们来看一看：

我们随机取三点，用黄点随机取的3个点：

 

 

 

 

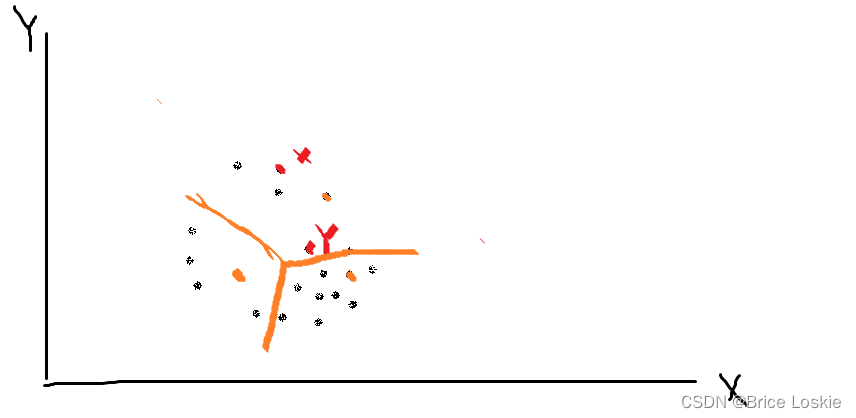
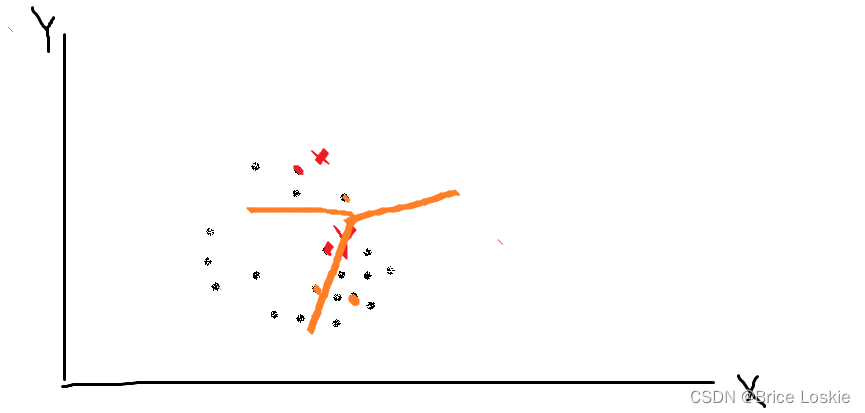
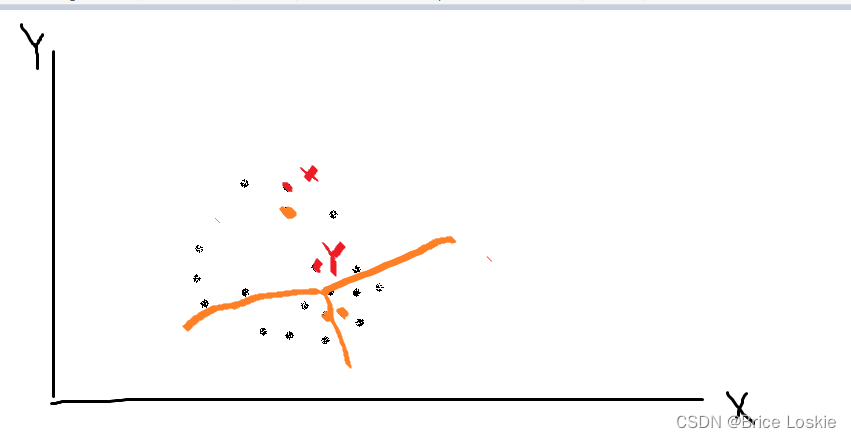
 如上图所示：X-Y有两次被分配到一起：所以X-Y核函数的距离为0.4

上面的划分方法是用的knn方法

用正规的数学表达来说就是：

我们照此方法，可以得到一个20×20的邻接表，存储了每个点到每个点的概率(相对于AHC算法中的欧氏距离)

2.点集合相似度

 

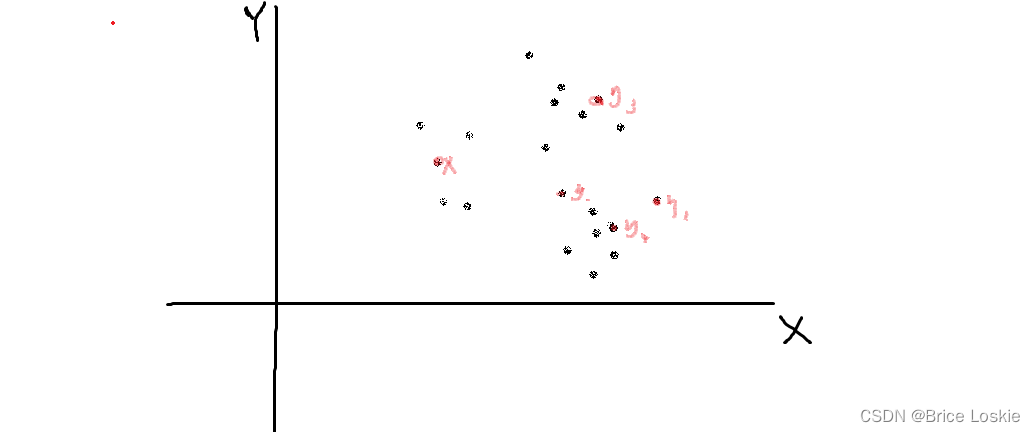
 如上图，找出一个x和4个y

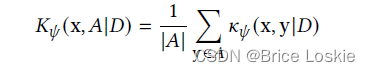
 A是的集合，x到A的核函数距离是x到所有的y的核函数距离和的平均。

3.特征映射

 

 

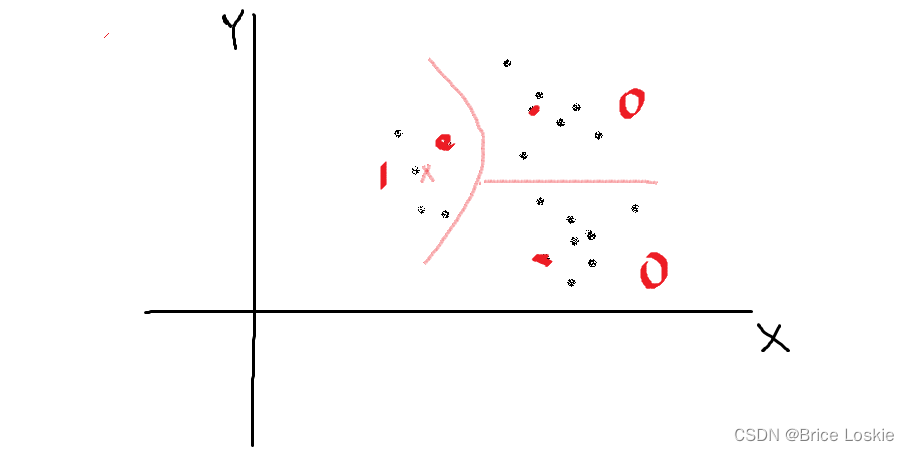
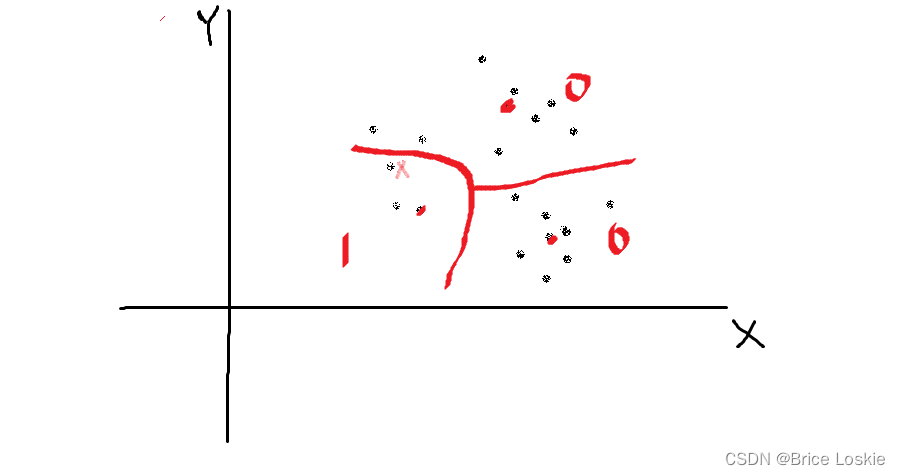
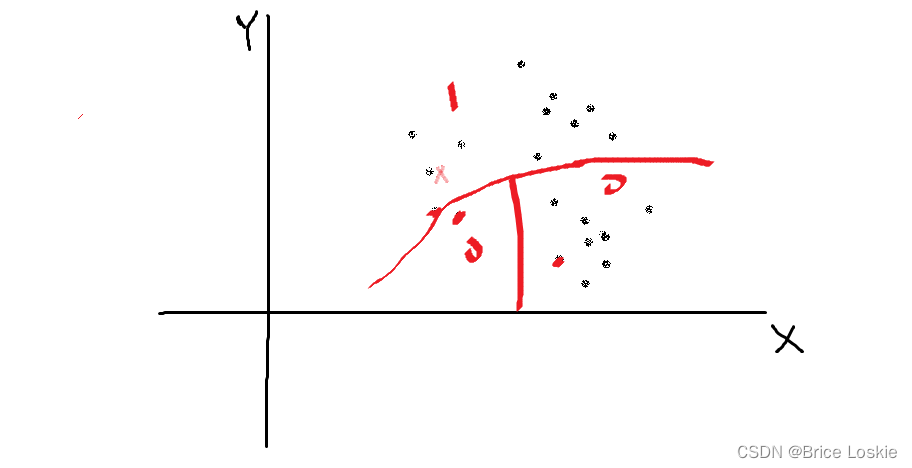
 如图每种划分H的每个分区都被1或者0映射，有X的分区映射为1，相反，没有x的分区映射为0

这是点集合相似度用映射的方法来表示的公式。

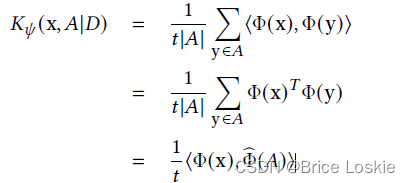
 是映射符号。