本文是Quantitative Methods and Analysis: Pairs Trading此书的读书笔记。

控制理论(control theory）是工程学的分支之一，主要应对工程系统控制的问题。比如控制汽车发动机的功率输出，稳定电动机的转速，控制“反应速率”（或化学过程的速度），通过所谓的控制变量（control variables)去控制系统。在控制汽车发动机的功率输出的例子中，控制变量可以是输入发动机的汽油量。

典型的控制系统的方法包括了规定数学模型来描述动态系统。这种模型通常用几个不同的式子表示。通过操纵模型中的变量实现控制。但是，现实中系统会有一些意想不到的波动、变化是无法使用一种确定的方法去建模。因而卡尔曼滤波被R.E.Kalman提出去解决这个问题。

卡尔曼滤波来自文章“A New Approach to Linear Filtering and Prediction Problems"。而Kalman的文章其中一个贡献就是提出系统状态（system state）的概念，或者说系统当前的状态。系统的状态表示为由不同的系统参数当前值组成的向量。向量本身是从系统上的一组观测值推导出来的，这些测量值又被转换成系统状态项（system-state terms）。这种转换通常被建模为线性方程。因此，进行观测的方法和将观测值转化为系统状态的方程式充分体现了系统状态的概念。

有了系统状态的概念后，看看使用系统状态去描述动态系统（dynamical system)。在卡尔曼滤波方法中，使用一系列的系统状态转移（即从一个系统状态转移到另一个系统状态）来对动态系统建模。这些转移（transistion)也被建模为线性方程。

接下来，为了有效地监控系统（出于控制的目的），对我们当前所处的状态以及我们预计在下一时间步骤中过渡到的状态进行评估是有必要的。换句话说，我们需要不断预测下一个系统状态并进行测量以验证预测得好不好。卡尔曼滤波器提供了一个方法来协调预测状态，然后进行测量这两个步骤得到的值，从而获得系统状态的最佳估计序列。这个方法把系统看作一系列的状态转移在当时是很颠覆的，开创了控制领域的一个新时代称为现代控制理论。

应用到风险套利的情形，我们可以用卡尔曼滤波方法来过滤观测到的spread价差中的噪声。

卡尔曼滤波方法还可以用来平滑一个随机游走。现在很多技术分析人员用所谓的移动平均（moving average)去平滑或者说过滤价格时间序列。这种使用移动平均的方法可以看作是在过滤了噪声之后尝试对股价时序进行估计（预测）。人们对移动平均线的普遍不满一直是，当价格走势发生剧烈而突然的变化时，移动平均线往往会滞后。而卡尔曼滤波帮助我们构造更好的平滑器（更好的平滑方法）。

---

卡尔曼滤波的过程可以概括为3个步骤：预测（prediction)，观测（observation)，协调或修正(correction)。

预测即根据系统当前的状态预测系统下一个状态，并且评估预测误差。

接下来，我们在经过一定时间后读取或者说观测系统的状态（系统现在转换到了新状态）。基于数学模型，把读取的信息转换为系统状态。同样，我们要评估观测误差。

下一步是协调两个状态估计（即预测状态和观测状态），并且要考虑两个相关误差的大小。即预测的估计值要根据观测值进行修正。因此，这被称为修正步骤。来自修正步骤的系统状态的协调估计是当前系统状态的最终估计。

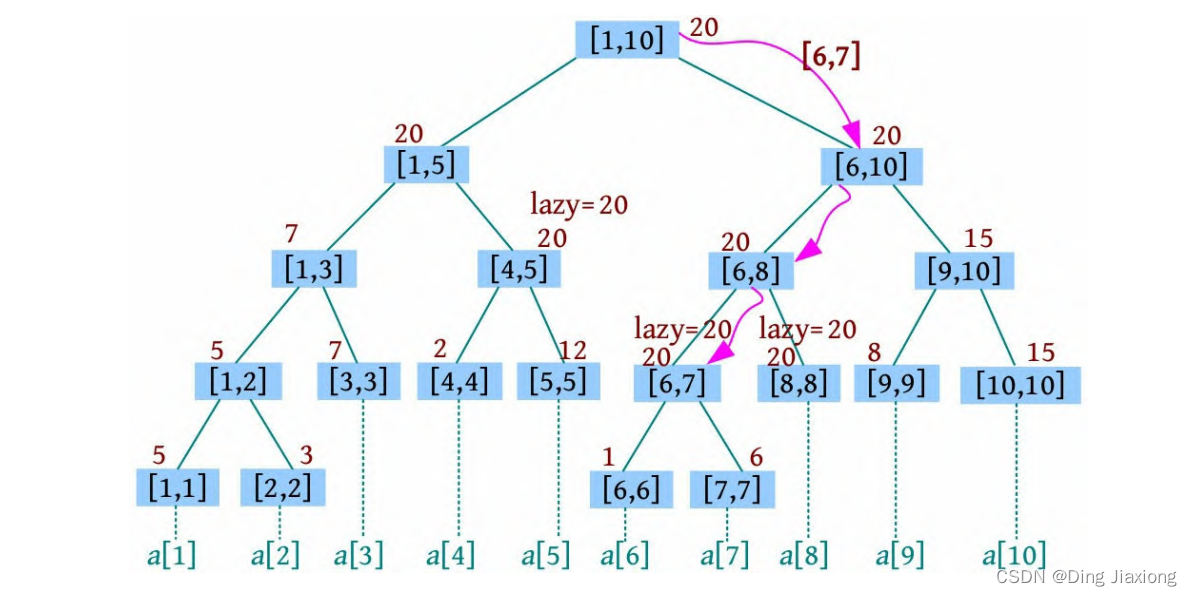
这样，我们去到下一个系统状态。然后，重复以上三个步骤继续估计下下个系统状态。卡尔曼滤波就是这样一个重复“预测-->修正”的方法。如下图：

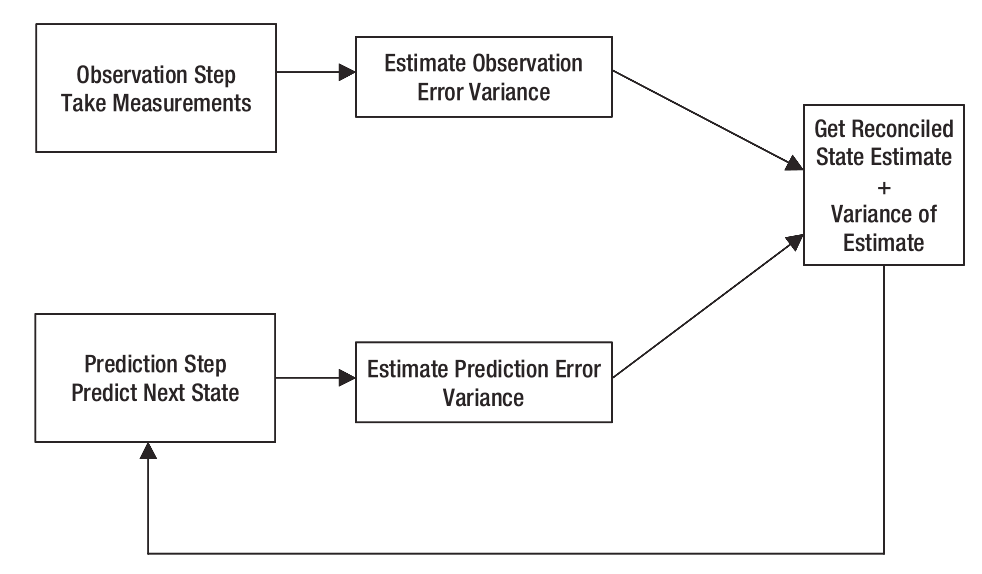
那么是如何修正预测值得的呢？我们可以把对下一个状态的预测值理解为期望的观测值(expected observation)，把这称为预测观测值（predicted observation）。修正状态在卡尔曼滤波器中表示为：

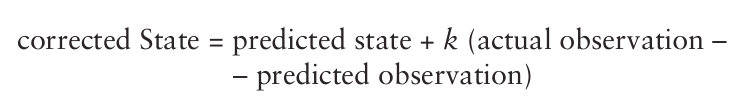
式子中，实际观测值（actual observation）和预测观测值（predcited observation)的差距称为observation innovation。称为Kalman gain卡尔曼增益。卡尔曼滤波方法规定了的取值为使得修正状态具有最小的误差方差。

卡尔曼还证明了在状态值和观测值的数学模型都是线性的，并且误差来自独立的高斯分布的情况下，该过程是最优的。

接下来看一下卡尔曼滤波步骤的正式规定：

表示在时间的状态。注意，状态可以是一个向量，说明这个状态是多维的。在卡尔曼滤波器中，用于预测时间的状态的数学模型是：

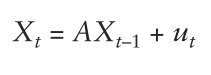
是一个矩阵，，分别表示在时间和时间的状态向量，是误差向量用来表示模型的不准确性。

表示在时间的观测值（即观测到的状态）。表示为：

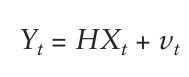
矩阵和是已知的。起初，根据到时间为止的状态信息，我们对时间的状态做一个预测，表示为。预测误差在一维状态的情况下表示为方差，在多维状态的情况中表示为协方差矩阵，用符号表示。类似地，观测误差在一维状态的情况下表示为方差，在多维状态的情况中表示为协方差矩阵，观测误差用表示。

这样卡尔曼滤波步骤的正式规定为：

这些步骤会在下一个时间步长重复执行。