1.常用手段
①区间对称,利用被积函数奇偶性
②放缩(利用常用不等式,结论等)
③将 1 转换成定积分
④直接算
⑤“拆区间,变量代换改区间再合并”
2.常用不等式
1.基本不等式
sinx < x < tanx (0 , Π/2) (几何或者夹逼证明)
ex >= 1 + x (-∞,+∞)(等价证明)
x/1+x < ln(1+x) <x (0,+∞) (拉格朗日中值定理证明)
2.绝对不等式
|a+b| <= |a| + |b|
3.均值不等式
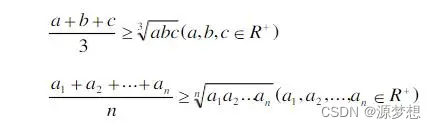
4.二项式展开式,可以用来放大缩小数列,求极限
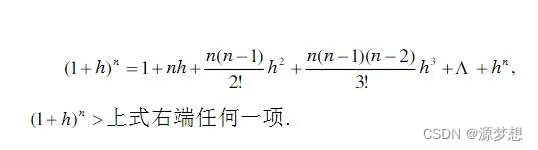
2.经典例题1
1,对称区间,被积函数直接有奇偶性
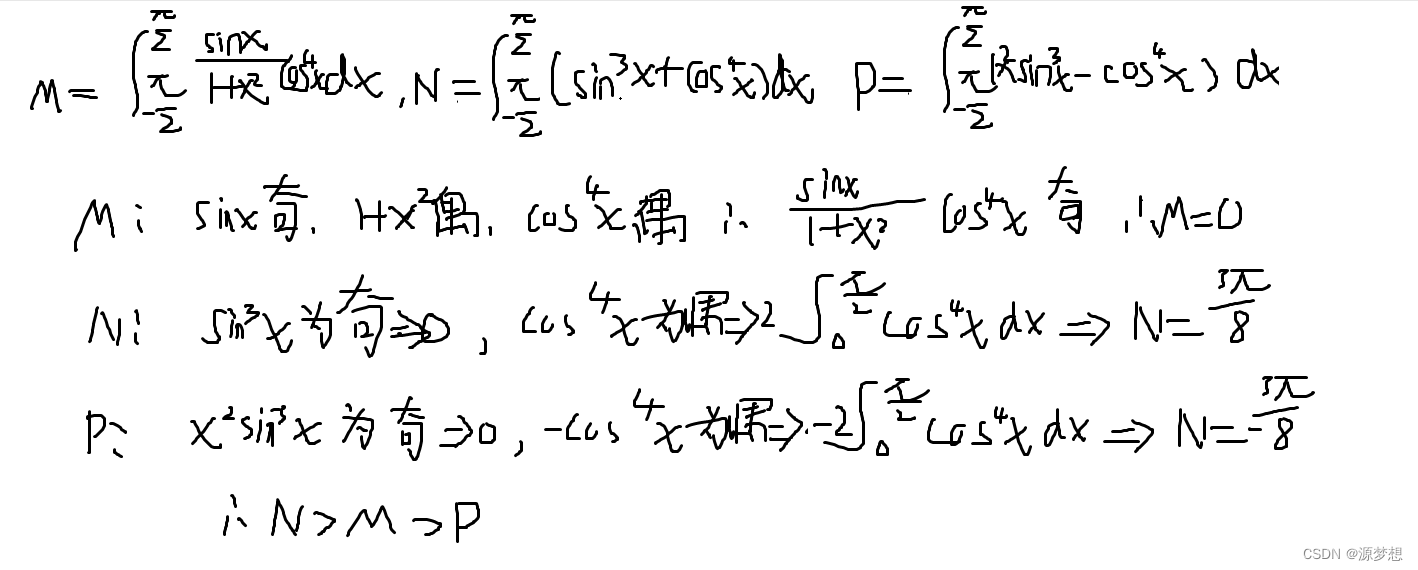
2.对称区间,被积函数没有奇偶性,用常用不等式,结论,放缩等手段创造奇偶性。
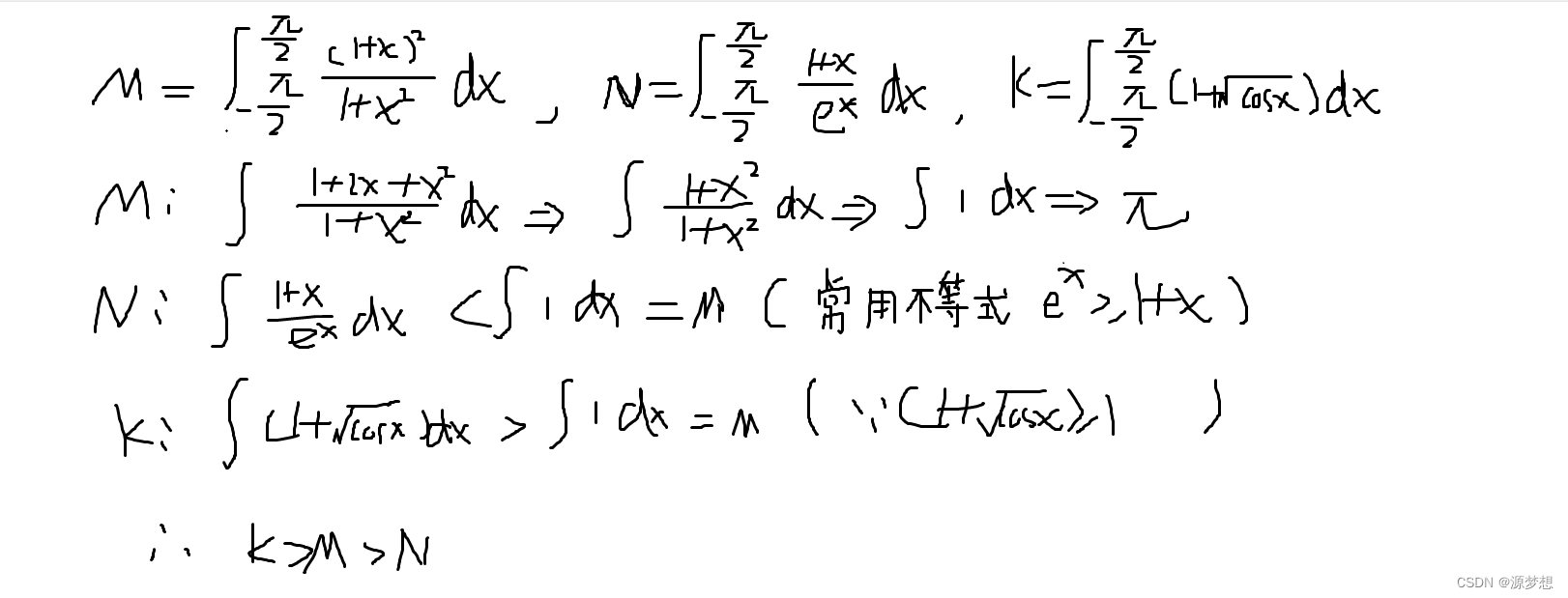
2.经典例题2
1.将 1 转换成定积分。
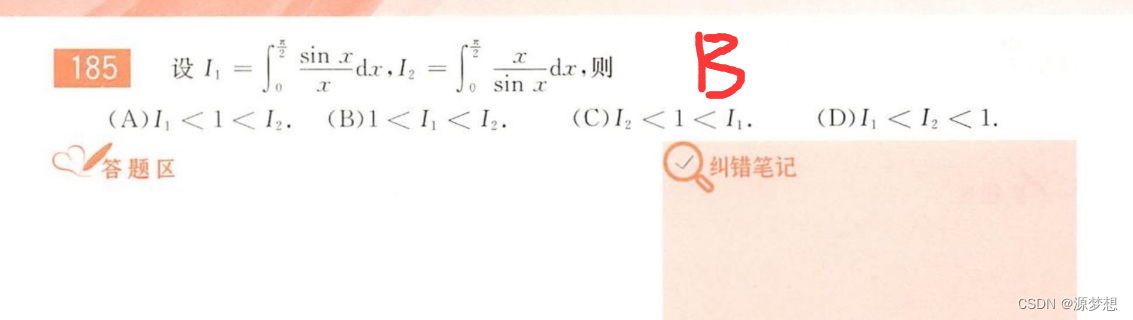
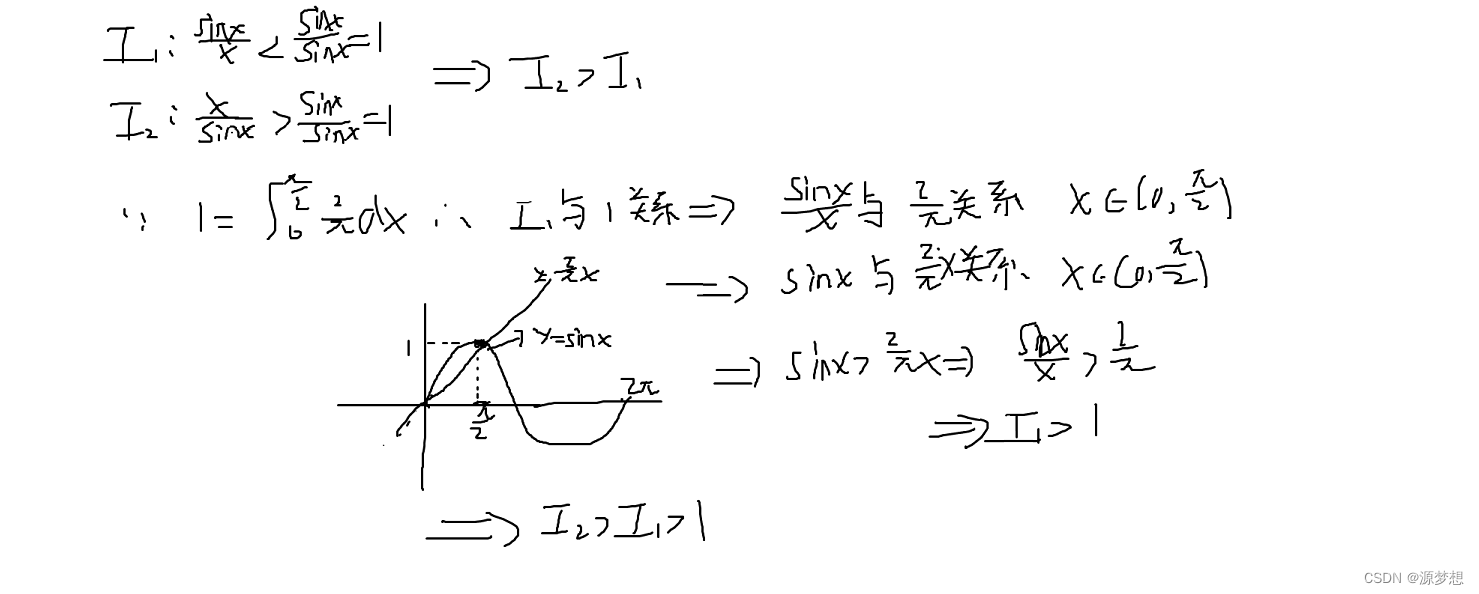
2.经典例题3
1.“拆区间,变量代换改区间再合并1”
C
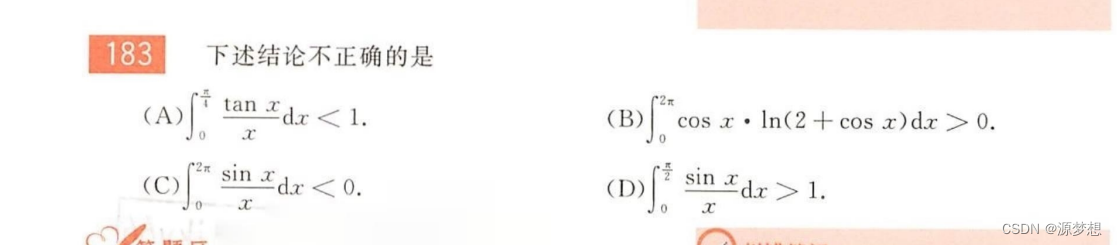

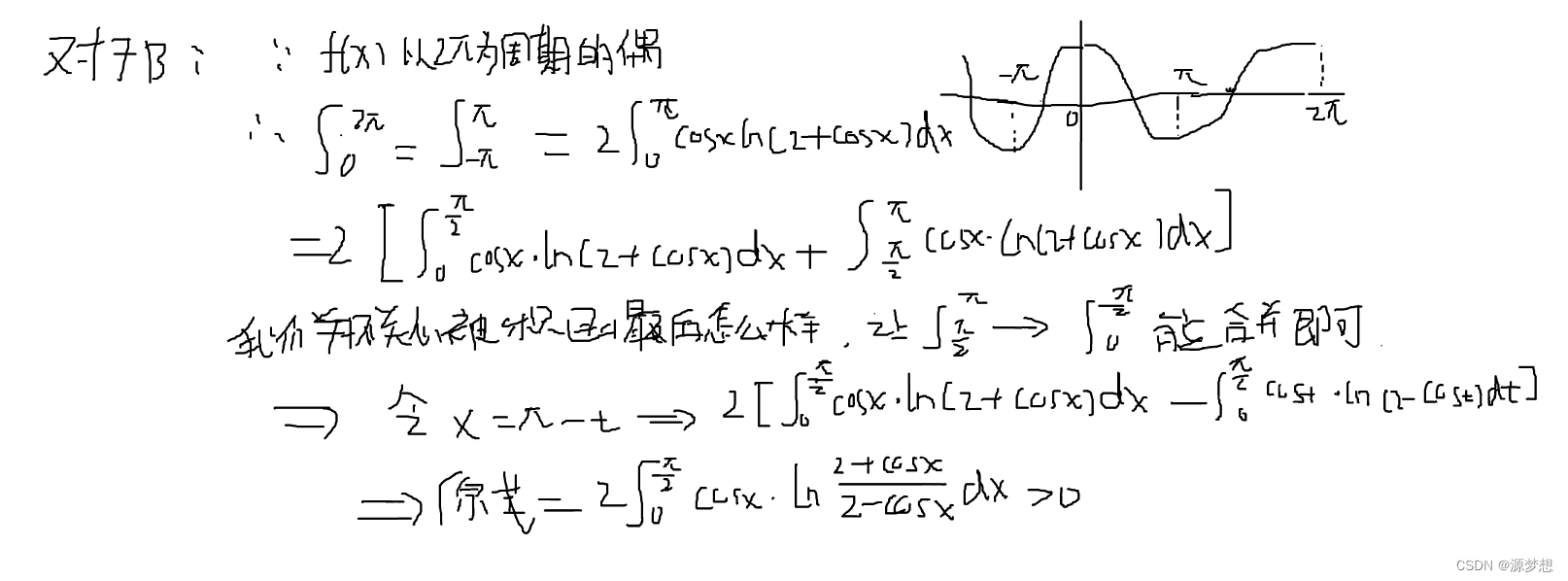




![[GFCTF 2021] day2](https://img-blog.csdnimg.cn/b1be61f140f8408f9e5e21fcf350aee5.png)