这一章讲移动机器人相关的内容。许久没有更新了,有人私聊我是不是烂尾了。写的这几篇屁文我本来是拿来当自己的笔记本的,不以为有人会认真看。没想到居然还有人追,真是受宠若惊。在这里深表感谢!一直没更新其实是因为年后的工作实在是太忙了,连休息的时间都没有,更何谈写这些博客。另外我还看到之前写的一些内容甚至我自己都没有印象了,看来还得抽时间再回顾一遍。
话不多说,开始吧:

开篇放了一个这样的公式:意为讲固定系s下的角速度、沿xy方向的线速度变换到body系下并用旋量表示。在2维平面中,角速度其实无所谓哪个系,因为尽管是body系,瞬间来说也是固定的,其旋转的角速度瞬间而言是相同的。而线速度,可以看出从s系到b系,是乘了一个二维的旋转矩阵Rbs,而从b系是乘了一个Rsb。
这要注意一下:标准的Rsb,第一列是cos,sin。回顾一下以前的知识:对绕轴旋转得到的旋转矩阵而言,对x,z轴旋转,除了把对应位置填成1,行和列其他位置填成0,剩下的第一列就是填cos,sin。写出了第一列,另一列就自然把sin取反即可。y则相反,头一列是cos,-sin。
轮式机器人类型
主要分为非完整(nonholonomic)类型和全向(omnidirectional)类型。
非完整类型主要受到Pfaffian速度约束,大意就是速度约束无法通过积分来转换成一个等效的位形约束,参见:【现代机器人学】学习笔记一:位形空间_grubler公式_zkk9527的博客-CSDN博客
而全向类型的又分为全向轮和麦克纳姆轮,书上有明确的图,就是一圈轮胎上还挂着横向的轮,全向轮的话横向的轮的旋转轴在车轮平面上,而麦克纳姆轮的旋转轴和轮的平面有一个夹角。
实际上,要实现全向移动,机器人底盘上至少需要有三个轮子,绕起来是一个圆,通过控制三个轮子的转速,才能实现全向功能。(为什么呢?因为我们移动机器人实际上是想生成三维底盘速度,即角速度和xy方向的线速度。我们既然不是非完整约束的轮子,三个自由度的输出,那我们就得需要三个自由度的输入,即三个轮子的转速)而我们图上的轮子:

它这个横向的轮子只是确保能横着转,这样不会对主动轮造成横向摩擦,并不是说上位机可以控制主动轮上面的一个一个小的滚轮主动运动,这点要注意。
和机械臂不同,轮式机器人的运动学,主要考虑车轮速度如何映射为机器人本体速度,而动力学则考虑车轮的扭矩如何映射为机器人的加速度。这章只考虑运动学的内容。实际上按我的工程经验而言,好像对移动机器人而言一般并不是很在意动力学,更重要的是避开障碍物。也许这些内容做自动驾驶的朋友们更关注,但目前我还没有接触过。
全向轮式机器人
建模
这本书很好,好就好在讲内容以前总是从宏观角度先说明,自己打算讲什么东西。让读者带着问题去继续读,总比稀里糊涂读下去好一些。
这里列出了两个关键问题:
1.车轮怎么转,才能使得底盘达到期望的速度?
2.根据车轮转速的极限,怎么得到底盘速度的极限?
好那让我们带着问题继续读下去。
单个全向轮是怎么运动的

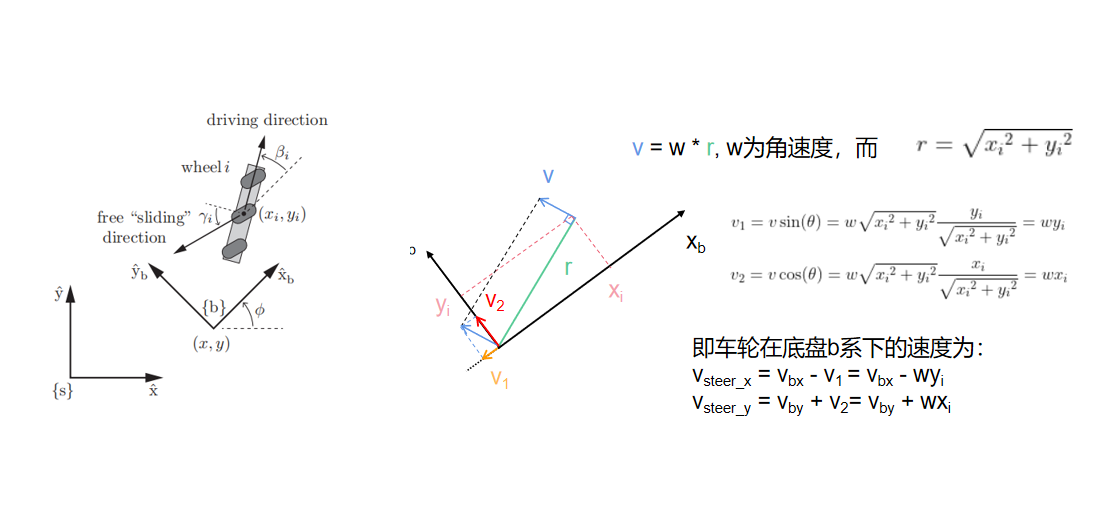
在说三个全向轮子组成的机器人的运动之前,我们需要先考虑单个轮子转起来会怎么样。如左一图所示,这个麦克纳姆轮上的被动轮,和主动轮的轴之间存在一个夹角γ,被动轮在转起来的时候,可能会发生一个“滑动”,这是被允许的。假设滑动的方向沿着左图的方向,因此我们可以得到如下的公式:

相信上面的公式大家都可以看明白,就是一个简单的几何关系。但是这个问题中呢,我们是想分清主次。我们事实上是想控制Vx,Vy的,但是我们这里只能控制主动速度Vdrive,因此需要解方程:

滑动速度Vslide是被动轮在转的,我们管不了,我们只能通过控制轮子的驱动角速度,来控制主动速度Vdrive:

因此我们想控制一个轮子的速度vx,vy的话,只要通过上式,控制主动轮的驱动角速度就可以了。
多个全向轮是如何带动底盘运动的
我们假设是第i个轮子的驱动角速度,
是期望的底盘速度,那么这里向做的就是计算出各个
,从而实现
。

书里二话不说,摆了一个公式。实际上这里摆快了,容易吓到读者。
现在我们不要急,从右到左一个一个看:
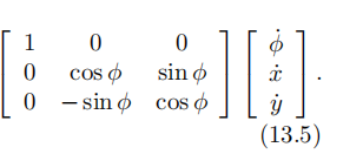
这一项是干嘛呢?别忘记我们开头的内容,是把s系下的线速度,通过Rbs,转换到body系下得到一个旋量速度。
这个公式难在第二个变换:

这是个什么玩意呢?看的让人一头雾水。
我们知道,这个东西得到一个3*1的向量,即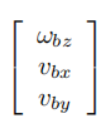 代表底盘在body系下的旋量。
代表底盘在body系下的旋量。
那左边再乘以 这样一个2*3的矩阵,会得到一个2*1的向量,目的是得到车轮在body系(也就是底盘坐标系)中xy方向的线速度。
这样一个2*3的矩阵,会得到一个2*1的向量,目的是得到车轮在body系(也就是底盘坐标系)中xy方向的线速度。
那这里我不得不放一个图,否则说不清楚:
假如蓝色的v是底盘瞬时的角速度引起的垂直于半径方向的线速度,我们要做的就是把它给拆分,得到xy分量上的速度,然后和原本xy方向的速度叠加在一起,得到
那么这时候 乘以
乘以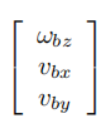 的含义就很清楚了。就是得到了车轮在body系下的线速度,去除了角速度的影响。
的含义就很清楚了。就是得到了车轮在body系下的线速度,去除了角速度的影响。
然后我们把车轮在body系下的速度,变换到车轮坐标系下,我们根据左图,可以看出有一个β的夹角。我们知道如果从A系到B系,如果根据右手坐标系,从A转到B的夹角为θ,那么旋转矩阵RAB为:
在上图中,从body系到车轮系的夹角为β,而我们已经有了body系下的线速度,因此,Rbody_steer 为
而Rsteer_body为:
即 中的第三个变换。
中的第三个变换。
这时得到了在车轮系下的线速度,我们要变成控制的驱动角速度,这是套用之前在 单个全向轮是怎么运动的 这部分的公式: ,我们采用向量的形式来写,就是:
,我们采用向量的形式来写,就是:
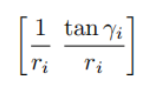 注意,这个里面它是一个1*2的向量,通过乘以右边的2*1的向量,得到一个1*1的角速度。可不能犯傻理解为这里是
注意,这个里面它是一个1*2的向量,通过乘以右边的2*1的向量,得到一个1*1的角速度。可不能犯傻理解为这里是啊。
这时候难点攻克下来了,我们这里化简,把H矩阵算出来,这样编码的时候就是一劳永逸,直接就可以从底盘期望速度得到各个车轮的速度了:
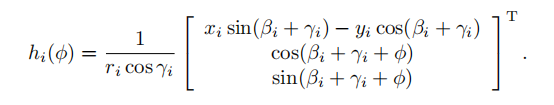
这个过程我就不想推了,毕竟不是在研究数学。
然后u就表示为:
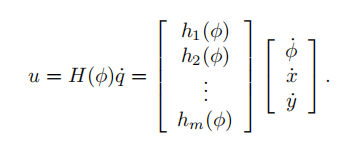
这里的u就是各个车轮的转速了,而不只是之前的ui代表第i个车轮的转速。
如果我们想让H中没有角度变量,那就是把

中的前三项合在一起,后两项合在一起:

这个的作用是,对车辆的构型可以起到指导作用,即选择车轮在底盘坐标系的位置,滑动方向,就可以合理选择,使得H(0)的秩为3。
那么到现在来说,实际上就完成了开篇的内容中的第一个重要问题:如何通过底盘的期望速度,计算得到各个车轮的转速。
那么根据上面得到的方法,再配合实际的机器人构型:

我们带入公式就可以得到实际的运动学模型:


那么上面的推导实际上就是授人以渔。
对于图示的四个麦克纳姆轮的全向小车,如果想沿着+x方向运动,所有车轮需要相同速度向前行驶。如果想沿着+y移动,1和3后驱动,2和4前驱动。如果想旋转,就是同侧相同驱动,另一侧反向。这个想想就可以理解。
第二个重要问题:根据车轮转速的极限,怎么得到底盘速度的极限?
我们知道,车轮速度是受到约束的:

那么我们就可以得到两个约束平面,只要在它之间的Vb就可以满足。
多个轮子,就是多个约束平面,构成的多面体,内部空间实际上就意味着在凸多面体内部的运动旋量都是可行的。
运动规划和反馈控制
对全向轮小车而言,好处就在于任何方向都可以直接移动。因此运动规划无需多讲,和前面的内容完全一致,参见:【现代机器人学】学习笔记九:运动规划_虚拟势场法_zkk9527的博客-CSDN博客
而反馈控制,也可以回顾一下:

通过这种方式来跟踪轨迹,其中q为传感器对实际位形的估计。我们在底层使用上面推导得到的公式,就可以把期望速度转化为车轮驱动速度进行控制了。
非完整约束轮式移动机器人
这个今天没有时间写了,明天继续,占坑。。
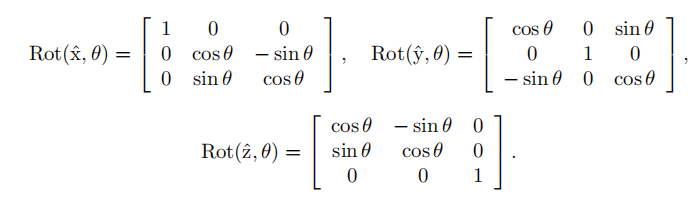


![[GFCTF 2021] day2](https://img-blog.csdnimg.cn/b1be61f140f8408f9e5e21fcf350aee5.png)