1143.最长公共子序列⭐️

• 题目链接：代码随想录

• 解题思路：
  1.dp数组：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp(i)[j]
  定义[0, i - 1]简化初始化逻辑
  2.递推公式：
  如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp(i - 1)[j - 1] + 1;
  如果text1[i - 1] 与 text2[j - 1]不相同，那么比较一下这两个的前一个元素的最长公共子串
  3.初始化：
  test1[0, i-1]和空串的最长公共子序列自然是0，所以dp(i)[0] = 0;
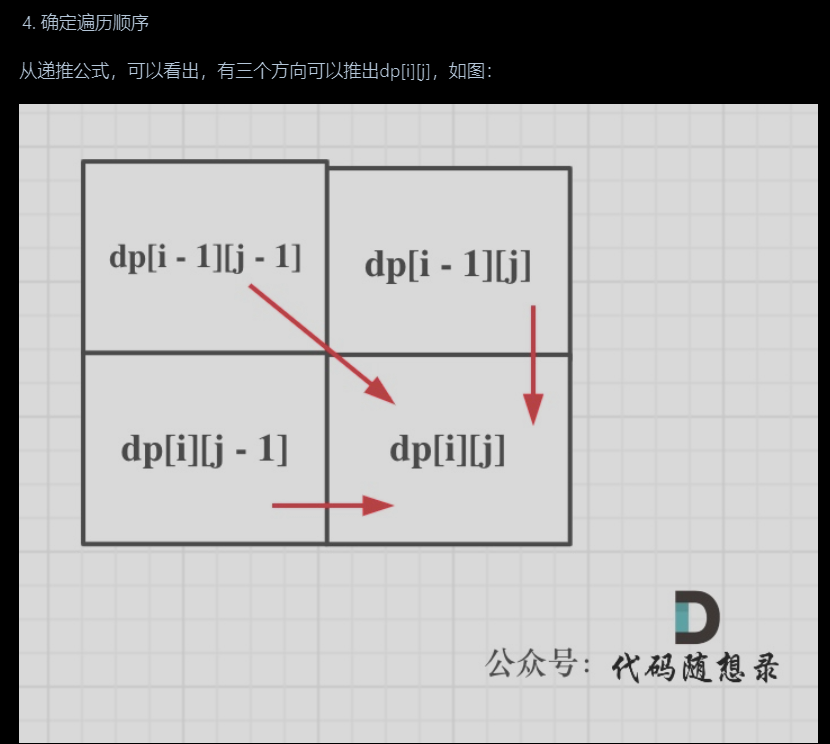
  4.遍历顺序：
  二维数组，本元素都由右上角的元素推导而来，所以一层一层的遍历

• 推导过程

  

public int longestCommonSubsequence(String text1, String text2) {
    //1.dp数组，dp[i][j]表示长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]
    int[][] dp = new int[text1.length() + 1][text2.length() + 1];
    for (int i = 1 ; i <= text1.length() ; i++) {
        char char1 = text1.charAt(i - 1);
        for (int j = 1; j <= text2.length(); j++) {
            char char2 = text2.charAt(j - 1);
            //递推公式
            if (char1 == char2) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    //2.返回dp数组
    return dp[text1.length()][text2.length()];
}

1035.不相交的线

直线不能相交，就是找两个串中相对顺序不变的子序列的问题

实际上是求两个字符串的最长公共子序列的长度

• 题目链接：代码随想录

public int maxUncrossedLines(int[] nums1, int[] nums2) {
    int len1 = nums1.length;
    int len2 = nums2.length;
    int[][] dp = new int[len1 + 1][len2 + 1];

    for (int i = 1; i <= len1; i++) {
        for (int j = 1; j <= len2; j++) {
            if (nums1[i - 1] == nums2[j - 1]) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }

    return dp[len1][len2];
}

53. 最大子序和 动态规划

1. 暴力解法：只需要先两层for循环确定两个数组起始位置，然后再来一个循环可以是for或者while，来从两个起始位置开始比较，取得重复子数组的长度

2. 本题动态规划就是记录下暴力解法的所有可能性结果下，以某下表结尾的连续子数组的最大长度。记忆状态换时间

• 题目链接：代码随想录

• 解题思路：
  1.dp数组：dp[i]：包括下标i（以nums[i]为结尾）的最大连续子序列和为dp[i]
  2.递推公式：
  递推公式推导来源：①dp[i - 1] + nums[i]，即：nums[i]加入当前连续子序列和②nums[i]，即：从头开始计算当前连续子序列和
  3.初始化：dp[0]应为nums[0]即dp[0] = nums[0]
  4.遍历顺序：从前向后遍历

• 推导过程：

  

public int maxSubArray(int[] nums) {
    if(nums.length == 1){
        return nums[0];
    }
    //1.定义dp数组，表示索引为i的元素的最大子序列和
    int[] dp = new int[nums.length];
    //2.初始化
    dp[0] = nums[0];
    int result = nums[0];
    for (int i = 1; i < nums.length; i++) {
        //递推公式
        dp[i] = Math.max(nums[i],dp[i - 1] + nums[i]);
        result = Math.max(result,dp[i]);
    }
    return result;
}