利用空档期时间学习一下计算机系统基础,以前对这些知识只停留在应试层面,今天终于能详细理解一下了。参考课程为南京大学袁春风老师的计算机系统基础MOOC,参考书籍也是袁老师的教材,这是我的听课+自查资料整理后的笔记
补码表示法
补码表示可以实现加减运算的统一,即用加法来实现减法运算。在计算机中,补码用来表示带符号整数。补码表示法也称“2-补码”( two’s complement)表示法,由符号位后跟上真值的模2"补码构成,因此,在介绍补码概念之前,先讲一下有关模运算的概念。
模运算(modular运算)
在一个模运算系统中,一个数与它除以“模”后的余数等价。在模运算系统中,若 A , B , M A,B,M A,B,M满足下列关系: A = B + K × M ( K 为整数) A=B+K\times M(K为整数) A=B+K×M(K为整数),则记为 A ≡ B ( m o d M ) A\equiv B(modM) A≡B(modM),即 A , B A,B A,B各除以 M M M后的余数相同,故称 B B B和 A A A为模 M M M同余。现实世界中的模运算系统比如:时钟是一种模12系统
假定钟表时针指向10点,要将它拨向6点, 则有两种拨法:
- 倒拨4格: 10 − 4 = 6 10- 4 = 6 10−4=6
- 顺拨8格: 10 + 8 = 18 ≡ 6 ( m o d 12 ) 10+8 = 18 ≡ 6(mod 12) 10+8=18≡6(mod12)
模12系统中:
10
−
4
≡
10
+
8
(
m
o
d
12
)
10- 4 ≡ 10+8(mod 12)
10−4≡10+8(mod12). 则,称8是- 4对模12的补码 (即:- 4的模12补码等于8)。同样有 -3 ≡ 9 (mod 12)
,
,
,-5 ≡ 7 (mod 12)$等
【结论1】一个负数的补码等于模减该负数的绝对值。比如-5的补码,模
12
−
∣
−
5
∣
=
7
12-|-5|=7
12−∣−5∣=7,所以-5的补码是7
【结论2】对于某一确定的模,某数减去小于模的另一数,总可以用该数加上另一数负数的补码来代替,比如模12系统中,
10
−
4
=
10
+
(
−
4
)
的补码
10-4 = 10 +(-4)的补码
10−4=10+(−4)的补码
12
−
∣
−
4
∣
=
8
12-|-4|=8
12−∣−4∣=8,所以-4的补码是8
即
10
−
4
≡
10
+
8
10-4 ≡ 10 + 8
10−4≡10+8
补码(2’s complement)的表示
现实世界的模运算系统举例
【例】“钟表”模运算系统,假定时针只能顺拨,从10点倒拨4格后是几点?
【解】
10
−
4
=
10
+
(
12
−
4
)
=
10
+
8
=
6
(
m
o
d
12
)
10- 4 = 10+(12- 4) = 10+8 = 6(mod 12)
10−4=10+(12−4)=10+8=6(mod12)
【例】“4位十进制数” 模运算系统,假定算盘只有四档,且只能做加法,则在算盘上计算9828-1928等于多少?
【解】由结论可知:
【结论2】对于某一确定的模,某数减去小于模的另一数,总可以用该数加上另一数负数的补码来代替
模为 1 0 4 10^{4} 104,则 9828 − 1928 = 9828 + ( 1 0 4 − 1928 ) = 9828 + 9072 = < 1 > 7900 = 7900 ( m o d 1 0 4 ) 9828-1928=9828+(10^{4}-1928)=9828+9072=<1>7900=7900(mod 10^{4}) 9828−1928=9828+(104−1928)=9828+9072=<1>7900=7900(mod104),取模即只留余数,高位<1>被丢弃!相当于只有低4位留在算盘上。
关于-1928的补码,可以不用这么复杂得求出,按位取反改为加法(正数)末位加1即可,在十进制数中(0,1,2,3,4,5,6,7,8,9),0的反数是9,1的反数是8,2的反数是7,3的反数是6,4的反数是5,按中心对称互相对应,由上述规则,-1928的按位取反改为加法(正数)末位加1的结果是8071+1=8072
计算机中的运算器是模运算系统
计算机是8位二进制加法器模运算系统
【例】计算 0111 1111 - 0100 0000
【解】0111 1111B - 0100 0000B相当于0111 1111B + 0100 0000B的补码
0100 0000B按位取反加1为1011 1111B + 0000 0001B=1100 0000B
则0111 1111B - 0100 0000B = 0111 1111B - 1100 0000B= <1> 0011 1111B,<1>被丢弃,只留余数,即结果为0011 1111B
【结论】一个负数的补码等于将对应正数补码各位取反、末位加一。
运算器适合用补码表示和运算
运算器只有有限位,假设为n位,则运算结果只能保留低n位,故可看成是个只有n档的二进制算盘,因此,其模为
2
n
2^{n}
2n
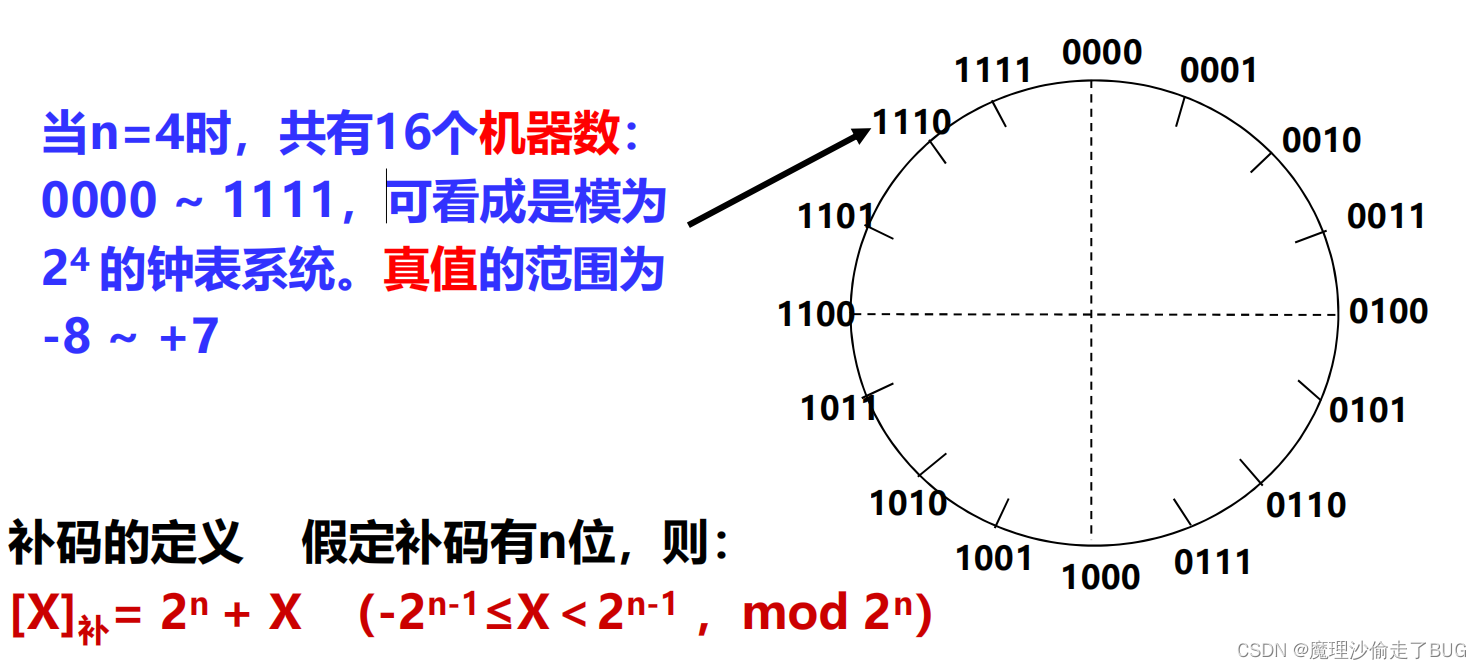
补码的定义
根据上述同余概念和数的互补关系,可引出补码的表示:正数的补码符号为0,数值部分是它本身;负数的补码等于模与该负数绝对值之差。因此,数
X
T
X_{T}
XT的补码可用如下公式表示:
(1)当
X
T
X_{T}
XT为正数时,
[
X
T
]
补
=
X
T
=
M
+
X
T
(
m
o
d
M
)
[X_{T}]_{补}=X_{T}=M+X_{T}(mod\space M)
[XT]补=XT=M+XT(mod M)
(2)当
X
T
X_{T}
XT为负数时,
[
X
T
]
补
=
M
−
∣
X
T
∣
=
M
+
X
T
(
m
o
d
M
)
[X_{T}]_{补}=M-|X_{T}|=M+X_{T}(mod\space M)
[XT]补=M−∣XT∣=M+XT(mod M)
综合(1)和(2),得到以下结论:对于任意一个数
X
T
X_{T}
XT,
[
X
T
]
补
=
M
+
X
T
(
m
o
d
M
)
[X_{T}]_{补}=M+X_{T}(mod\space M)
[XT]补=M+XT(mod M)
对于具有一位符号位和
n
−
1
n-1
n−1位数值位的
n
n
n位二进制正数的补码来说,其补码定义如下:
[
X
T
]
补
=
2
n
+
X
T
(
−
2
n
−
1
≤
X
T
<
2
n
−
1
,
m
o
d
2
n
)
[X_{T}]_{补}=2^{n}+X_{T}(-2^{n-1}\le X_{T}<2^{n-1}, mod\space 2^{n})
[XT]补=2n+XT(−2n−1≤XT<2n−1,mod 2n)
【注】用大白话解释上面的理论就是,正数的补码就是原码,负数的补码是按位取反后再加1.
求特殊数的补码