前言

2023-5-3 22:12:46

以下内容源自《【编译原理】》
仅供学习交流使用

推荐

第四章 作业（123）【编译原理】

第五章 作业

1

1.令文法G为:
E→E+T|T
T→T*F|F
F→(E)|i

证明E+T*F是它的一个句型,指出这个句型的所有短语,直接短语和句柄。

E+T*F是文法G的一个句型
语法树如下：

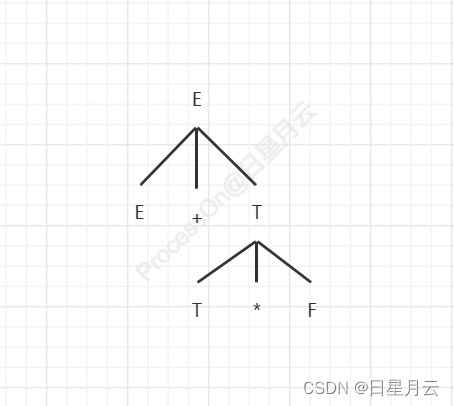
短语：E+T*F,T*F
直接短语：T*F
句柄：T*F

2

2.考虑下面的表格结构文法G2:
S->a|∧|(T)
T→T，S|S
(1)给出(a，(a，a))和(((a，a)，∧，(a))，a)的最左和最右推导。
(2)指出(((a，a)，∧，(a))，a)的规范归约及每一步的句柄。根据这个规范归约,给出“移进-归约”的过程,并给出它的语法树自下而上的构造过程。

(1) (a，(a，a))
最左推导：S=>(T)=>(T，S)=>（S，S）=>(a，S)=>(a，(T))=>(a，(T，S))=>(a，(S，S))=>(a，(a，S))=>(a，(a，a))
最右推导：S=>(T)=>(T，S)=>(T，(T))=>(T，(T，S))=>(T，(T，a))=>(T，(S，a))=>(T，(a，a))=>(S，(a，a))=>(a，(a，a))
(2)(((a，a)，∧，(a))，a)
最左推导：S=>(T)=>(T，S)=>(S，S)=>((T)，S)=>((T，S)，S)=>((T，S，S)，S)
=>((S，S，S)，S)=>(((T)，S，S)，S)=>(((T，S)，S，S)，S)=>(((S，S)，S，S)，S)=>(((a，S)，S，S)，S)
=>(((a，a)，S，S)，S)=>(((a，a)，∧，S)，S)=>(((a，a)，∧，(T))，S)=>(((a，a)，∧，(S))，S)
=>(((a，a)，∧，(a))，S)=>(((a，a)，∧，(a))，a)
最右推导：S=>(T)=>(T，S)=>(T，a)=>(S，a)=>((T)，a)=>((T，S)，a)=>((T，(T))，a)=>((T，(S))，a)
=>((T，(a))，a)=>((T，S，(a))，a)=>((T，∧，(a))，a)=>((S，∧，(a))，a)=>(((T)，∧，(a))，a)
=>(((T，S)，∧，(a))，a)=>(((T，a)，∧，(a))，a)=>(((S，a)，∧，(a))，a)=>(((a，a)，∧，(a))，a)

(2)
(((a，a)，∧，(a))，a)的规范归约：
	最右推导倒着来
具体可见符号栈+输入串的变化：
	共17步归约：6,7,10,11,13,14,17,18,22,23,25,26,28,29,32,33,35
	
(((a，a)，∧，(a))，a)：“移进-归约”的过程
步骤		符号栈				输入串 						操作			说明
1		#					(((a，a)，∧，(a))，a)# 		预备
2		#(					((a，a)，∧，(a))，a)# 		进
3		#((		    		(a，a)，∧，(a))，a)# 		进
4		#(((				a，a)，∧，(a))，a)# 			进
5		#(((a				，a)，∧，(a))，a)# 			进
6		#(((S				，a)，∧，(a))，a)# 			归			 S->a
7		#(((T				，a)，∧，(a))，a)# 			归			 T->S
8		#(((T，				a)，∧，(a))，a)# 			进	
9		#(((T，a			)，∧，(a))，a)# 				进		
10		#(((T，S			)，∧，(a))，a)# 				归	 		 S->a
11		#(((T				)，∧，(a))，a)# 				归	 		 T->T,S
12		#(((T)				，∧，(a))，a)# 				进
13		#((S				，∧，(a))，a)# 				归			 S->(T)
14		#((T				，∧，(a))，a)# 				归			 T->S
15		#((T，				∧，(a))，a)# 				进			
16		#((T，∧				，(a))，a)# 					进	
17		#((T，S				，(a))，a)# 					归			 S->∧
18		#((T				，(a))，a)# 					归			 T->T，S
19		#((T，				(a))，a)# 					进			 
20		#((T，(				a))，a)# 					进			 
21		#((T，(a			))，a)# 					进	
22		#((T，(S			))，a)# 					归			 S->a
23		#((T，(T			))，a)# 					归			 T->S
24		#((T，(T)			)，a)# 						进			
25		#((T，S				)，a)# 						归		 	 S->(T)		
26		#((T				)，a)# 						归			 T->T，S
27		#((T)				，a)# 						进			 
28		#(S					，a)# 						归			 S->(T)	
29		#(T					，a)# 						归			 T->S
30		#(T，				a)# 						进			  
31		#(T，a				)# 							进
32		#(T，S				)# 							归			 S->a
33		#(T					)# 							归			 T->T，S
34		#(T)				# 							进			
35		#S					# 							归			 S->(T)	
36		#S					# 							接受

(((a，a)，∧，(a))，a)语法树如下

3

3.(1)计算练习2文法G2的FIRSTVT 和 LASTVT。
(2)计算G2的优先关系。G2是一个算符优先文法吗?
(3)计算G2的优先函数。
(4)给出输入串(a，(a，a))的算符优先分析过程。

(1)文法G2的FIRSTVT 和 LASTVT。
FIRSTVT(S)={a ∧ (}          LASTVT(S)={a ∧ )}
FIRSTVT(T)={a ∧ ( ，}      LASTVT(T)={a ∧ ) ，}
2)G2的优先关系矩阵：
	a	^	(	)	,	#
a				>	>	>
^				>	>	>
(	<	<	<	=	<
)				>	>	>
,	<	<	<	>	>
#	<	<	<			=
G2是一个算符优先文法
(4)输入串(a，(a，a))的算符优先分析过程：
步骤		符号栈		输入串 			操作			说明
（1）	#			(a，(a，a))#		预备
（2）    #(  		a，(a，a))#	    移进			[#][(]=<
（3）	#(a			，(a，a))#	    移进			[(][a]=<		
（4）	#(T 		，(a，a))#	    归约			[a][，]=>
（5）	#(T， 		(a，a))#	    移进			[(][，]=<
（6）	#(T，(		a，a))#	    	移进			[，][(]=<
（7）	#(T，(		a，a))#	    	移进			[(][a]=<
（8）	#(T，(a		，a))#	    	移进			[(][a]=<
（9）	#(T，(T		，a))#	    	归约			[a][，]=>
（10）	#(T，(T，	a))#	    	移进			[(][，]=<
（11）	#(T，(T，a	))#	    		移进			[，][a]=<
（12）	#(T，(T，S	))#	    		归约			[a][)]=>
（13）	#(T，(T)	)#	    		移进			[(][)]==
（14）	#(T，S		)#	    		归约			[)][)]=>
（15）	#(T			)#	    		归约			[，][)]=>
（16）	#(T)		#	    		移进			[(][)]==
（17）	#S			#	    		归约			[)][#]=>
（18）	#S#				    	 	接受		

2023-5-7 00:00:54

随堂练习

2023-5-3 22:12:50

课前热身04-17

1(多选题) 语法分析按照分析的方向分为：
A. 自上而下的语法分析
B. 自下而上的语法分析
C. 自左而右的语法分析
D. 自右而左的语法分析

正确答案: AB 我的答案: AB

2(简答题) 有文法G:
E—>T|E+T
T—>F|T*F
F—>（E）|i

请说明句型E+T*F+i的短语，直接短语和句柄。

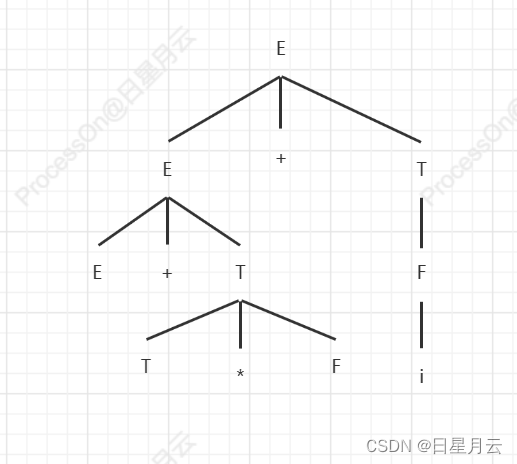
短语：E+T*F+i,E+T*F,T*F,i
直接短语：T*F,i
句柄：T*F

随堂练习04-17

1(简答题) 请构造该文法中所有非终结符的LASTVT集

E->E+T|T
T->T*F|F
F->(E)|i

	+ 	* 	( 	) 	i
E	1	1		1	1
T		1 		1 	1
F				1	1

课前热身04-24

1(单选题) 若a、b均为终结符，且a的优先级低于b，则说明:
A. 推导的符号串中，a位于b之前，a先于b被规约
B. 推导的符号串中，a位于b之前，b先于a被规约
C. 推导的符号串中，a位于b之后，a先于b被规约
D. 推导的符号串中，a位于b之后，b先于a被规约，也有可能同时被规约

正确答案: B 我的答案: B

2(判断题) 在算符优先分析中，待分析串的界符#，其优先级一定低于文法所有终结符号。
对
错

正确答案: 错 我的答案: 错

3必答 (简答题) 已知文法G[S]:
S → a|^|(T)
T → T,S|S
非终结符的FIRSTVT、LASTVT集如下所示：
FIRSTVT(S)={a ^ (} LASTVT(S)={a ^ )}
FIRSTVT(T)={a ^ ( ，} LASTVT(T)={a ^ ) ，}
请构造文法G的优先关系矩阵。

	a	^	(	)	,	#
a				>	>	>
^				>	>	>
(	<	<	<	=	<
)				>	>	>
,	<	<	<	>	>
#	<	<	<			=

2023-5-3 22:22:20

最后

2023-5-7 00:01:02

你对我百般注视，
并不能构成万分之一的我，
却是一览无余的你。

祝大家逢考必过
点赞收藏关注哦