4943. 方格迷宫 - AcWing题库
1、题目
给定一个 n 行 m 列的方格矩阵。
行从上到下依次编号为 1∼n,列从左到右依次编号为 1∼m。
第 i 行第 j 列的方格表示为 (i,j)。
矩阵中的方格要么是空地(用 . 表示),要么是陷阱(用 # 表示)。
初始时,你位于方格 (x₁,y₁),你需要前往方格 (x₂,y₂)。
每次移动,你可以任选上、下、左、右四个方向之一,并沿该方向移动 1∼k 步。
从一个方格移动至相邻方格视为一步。
但是,你要保证在你的移动过程中不能走出矩阵,也不能进入陷阱方格。
请你计算从方格 (x₁,y₁) 移动至方格 (x₂,y₂),所需要的最少移动次数。
保证方格 (x₁,y₁) 和方格 (x₂,y₂) 都是空地。
方格 (x₁,y₁) 和方格 (x₂,y₂) 可能是同一个方格。
注意:注意区分本题中移动次数与移动步数的区别。
输入格式
第一行包含三个整数 n,m,k。
接下来 n 行,每行包含 m 个字符,其中第 i 行第 j 个字符,要么是 .,表示方格 (i,j) 是空地;要么是 #,表示方格 (i,j) 是陷阱。
最后一行包含四个整数 x₁,y₁,x₂,y₂。
输出格式
一个整数,表示所需要的最少移动次数。
如果无法从方格 (x₁,y₁) 移动至方格 (x₂,y₂),则输出 -1。
数据范围
前 6 个测试点满足 1≤n,m≤10。
所有测试点满足 1≤n,m,k≤1000,1≤x₁,x₂≤n,1≤y₂,y₂≤m。
输入样例1:
3 4 4
....
###.
....
1 1 3 1
输出样例1:
3
输入样例2:
3 4 1
....
###.
....
1 1 3 1输出样例2:
8
输入样例3:
2 2 1
.#
#.
1 1 2 2
输出样例3:
-12、题目解读
走迷宫_牛客题霸_牛客网 (nowcoder.com)
牛客网这题就是正常,普通求解最短步数的迷宫问题,而这题添加了一个条件:每次移动,你可以任选上、下、左、右四个方向之一,并沿该方向移动 1∼k 步。这称为 一次移动。
我们使用BFS去正常解答这道题目时间复杂度为O(nmk)最大为10⁹,这就会超时。
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
public class Main {
static int n,m,k,x1,x2,y1,y2;
static char[][] ch;
static int[][] move ={{0,1},{0,-1},{1,0},{-1,0}};//四个方向,偏移量
static int inf=0x3f3f3f3f;//初始化移动次数
static int[][] ans;//记录移动次数
public static void main(String[] args){
Scanner sc=new Scanner(System.in);
n=sc.nextInt();
m=sc.nextInt();
k=sc.nextInt();
ch =new char[n][];
ans =new int[n][m];
for(int i=0;i<n;i++){
ch[i]=sc.next().toCharArray();
}
x1=sc.nextInt()-1;
y1=sc.nextInt()-1;
x2=sc.nextInt()-1;
y2=sc.nextInt()-1;
for(int i=0;i<n;i++){//初始化移动次数
Arrays.fill(ans[i],inf);
}
System.out.println(bfs());
}
public static int bfs(){
ans[x1][y1]=0;
Queue<int[]> q=new LinkedList<>();
q.add(new int[]{x1,y1,0});
while(!q.isEmpty()){
int[] a =q.poll();
for(int[] mo :move){//四个方向
for(int i=1;i<=k;i++){//移动一次:移动1-k步
int x=a[0]+mo[0]*i,y=a[1]+mo[1]*i;
if(x<0||x==n||y<0||y==m||ch[x][y]=='#'){//不能出去,不能跨越陷阱
break;
}
if(ans[x][y]>a[2]+1){//修改移动次数
ans[x][y]=a[2]+1;
q.add(new int[]{x,y,a[2]+1});
}
}
}
}
//走完整个地图,判断目的地是否可以走到
return ans[x2][y2]==inf?-1:ans[x2][y2];
}
}

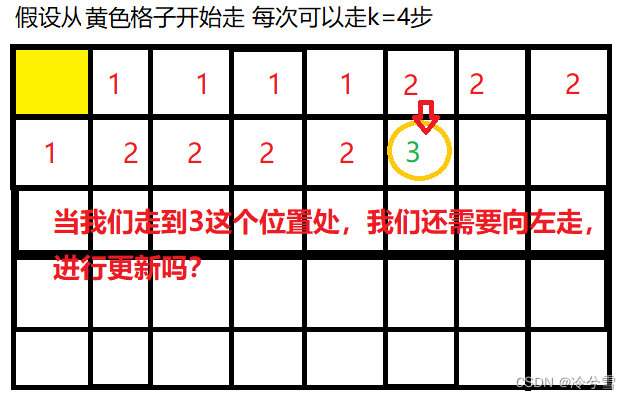
我们需要优化代码,看下面图:
所以我们应该 更新到格子发现不是最优,就应该停止。这样时间复杂度就退化到了O(nm)
需要在判断条件处新加:ans[x][y]<a[2]+1
3、代码
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
public class Main {
static int n,m,k,x1,x2,y1,y2;
static char[][] ch;
static int[][] move ={{0,1},{0,-1},{1,0},{-1,0}};//四个方向,偏移量
static int inf=0x3f3f3f3f;//初始化移动次数
static int[][] ans;//记录移动次数
public static void main(String[] args){
Scanner sc=new Scanner(System.in);
n=sc.nextInt();
m=sc.nextInt();
k=sc.nextInt();
ch =new char[n][];
ans =new int[n][m];
for(int i=0;i<n;i++){
ch[i]=sc.next().toCharArray();
}
x1=sc.nextInt()-1;
y1=sc.nextInt()-1;
x2=sc.nextInt()-1;
y2=sc.nextInt()-1;
for(int i=0;i<n;i++){//初始化移动次数
Arrays.fill(ans[i],inf);
}
System.out.println(bfs());
}
public static int bfs(){
ans[x1][y1]=0;
Queue<int[]> q=new LinkedList<>();
q.add(new int[]{x1,y1,0});
while(!q.isEmpty()){
int[] a =q.poll();
for(int[] mo :move){//四个方向
for(int i=1;i<=k;i++){//移动一次:移动1-k步
int x=a[0]+mo[0]*i,y=a[1]+mo[1]*i;
//不能出去,不能跨越陷阱,还有更新到格子发现不是最优,就应该停止
if(x<0||x==n||y<0||y==m||ch[x][y]=='#'||ans[x][y]<a[2]+1){
break;
}
if(ans[x][y]>a[2]+1){//修改移动次数
ans[x][y]=a[2]+1;
q.add(new int[]{x,y,a[2]+1});
}
}
}
}
//走完整个地图,判断目的地是否可以走到
return ans[x2][y2]==inf?-1:ans[x2][y2];
}
}