搜索旋转排序数组

news2025/1/11 19:56:22

题目链接

搜索旋转排序数组

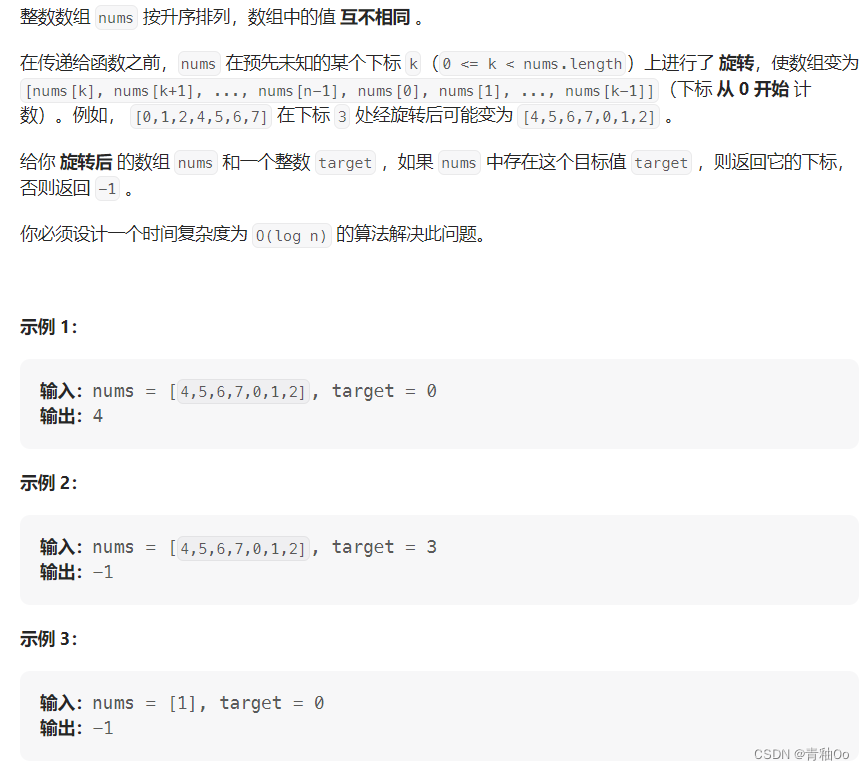
题目描述

注意点

nums 中的每个值都独一无二
题目数据保证 nums 在预先未知的某个下标上进行了旋转

解答思路

因为本题数组基本递增（仅在某个位置进行旋转），可以看作由两个递增的数组组合而成，所以要想在O(log n)的时间复杂度解决本题初始想到的是使用二分查找
但是本题并不是严格递增的，所以在对中点元素判断与目标值关系的同时，还要判断该位置是否是旋转后的数组位置以及与目标值之间的关系
相较于严格递增数组二分查找mid位置仅有两种情况，本题旋转一次二分查找会出现四种情况，如下：
（1） mid处元素小于数组第一个元素，目标值小于数组第一个元素，则target在mid左侧
（2） mid处元素小于数组第一个元素，目标值大于数组第一个元素，则target在mid右侧
（3） mid处元素大于数组第一个元素，目标值小于数组第一个元素，则target在mid右侧
（4） mid处元素大于数组第一个元素，目标值小于数组第一个元素，则target在mid左侧

代码

class Solution {
    public int search(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int mid = (left + right) / 2;
            if (target == nums[mid]) {
                return mid;
            }
            if (nums[mid] < nums[0] && target >= nums[0]) {
                nums[mid] = Integer.MAX_VALUE;
            }
            if (nums[mid] >= nums[0] && target < nums[0]) {
                nums[mid] = Integer.MIN_VALUE;
            }
            if (nums[mid] < target) {
                left = mid + 1;
            }
            if (nums[mid] > target) {
                right = mid - 1;
            }
        }
        return -1;
    }
}