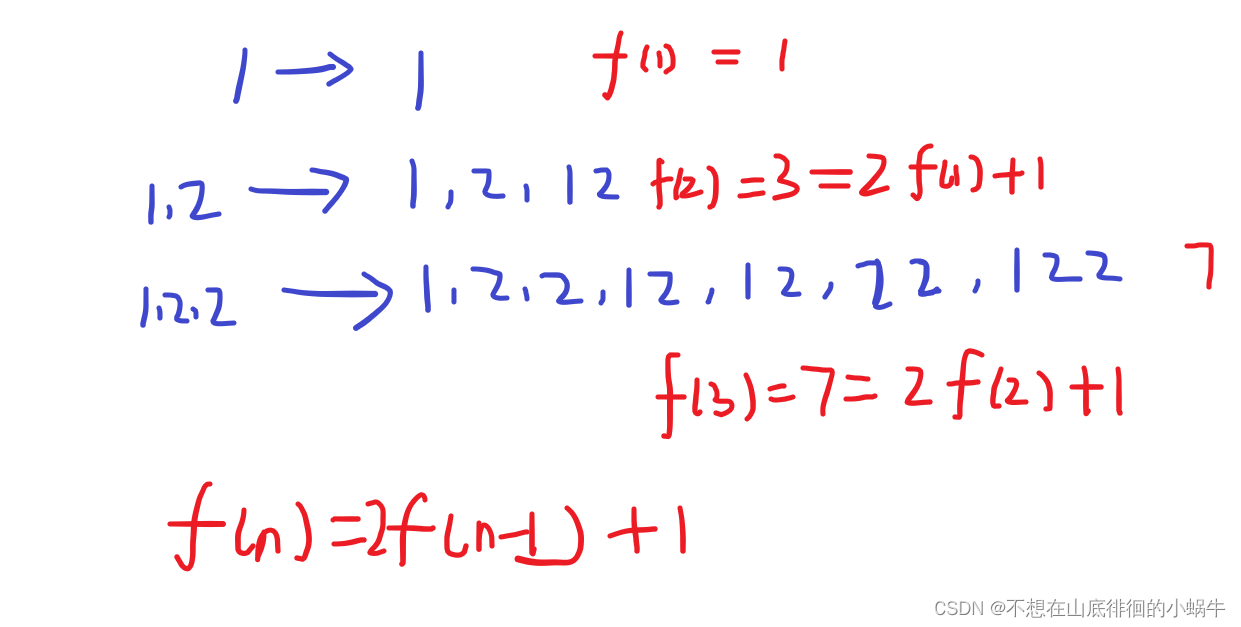目录链接：

力扣编程题-解法汇总_分享+记录-CSDN博客

GitHub同步刷题项目：

https://github.com/September26/java-algorithms

原题链接：力扣

描述：

有两种形状的瓷砖：一种是 2 x 1 的多米诺形，另一种是形如 "L" 的托米诺形。两种形状都可以旋转。

给定整数 n ，返回可以平铺 2 x n 的面板的方法的数量。返回对 109 + 7 取模 的值。

平铺指的是每个正方形都必须有瓷砖覆盖。两个平铺不同，当且仅当面板上有四个方向上的相邻单元中的两个，使得恰好有一个平铺有一个瓷砖占据两个正方形。

示例 1:

输入: n = 3
输出: 5
解释: 五种不同的方法如上所示。

示例 2:

输入: n = 1
输出: 1

提示：

• 1 <= n <= 1000

解题思路：

* 解题思路：
* 这一定是一道动态规划的题，如果我们去掉L型，那么就是一个斐波那契额数列，F(n)=F(n-1)+F(n-2)
* 加上L形状，我们仍然可以按照这个思路来。
* 开头只有四种可能，-，=，L,「。
* -和=开头的，我们可以归结为斐波那契额数列，f(n)=f(n-1)+f(n-2)
* L和「开头的，我们可以归结为一类问题，使用F(n)来表示，所以可以转换为f(n)=f(n-1)+f(n-2)+F(n)
* 我们再来看下F(n)怎解决？
* L开头的话，只有两种可能：
* L开头，以┐结尾，中间包含若干-形，其数量为f(n-3)+f(n-5)+f(n-7)...
* L开头，以」结尾，中间包含若干-形状，其数量为f(n-4)+f(n-6)+f(n-8)...
* 两种类型累加，就是F(n)的数量。
* 最后，每次计算对值求模，得到我们想要的结果

代码：

public class Solution790 {

    Map<Integer, Integer> fMap = new HashMap<>();
    int flag = 10_0000_0000 + 7;

    public int numTilings(int n) {
        fMap.put(0, 1);
        fMap.put(1, 1);
        fMap.put(2, 2);
        int index = 3;
        while (index <= n) {
            int indexValue = fMap.get(index - 1) % flag + fMap.get(index - 2) % flag;
            indexValue = indexValue % flag;
            indexValue += (2 * F(index)) % flag;
            indexValue = indexValue % flag;
            fMap.put(index, indexValue);
            index++;
        }
        return fMap.get(n);
    }

    private int F(int index) {
        //L开头，」结尾
        int sum = 0;
        for (int i = 0; i <= index - 3; i += 2) {
            sum += fMap.get(index - 3 - i) % flag;
            sum = sum % flag;
        }
        if (index <= 3) {
            return sum;
        }
        for (int i = 0; i <= index - 4; i += 2) {
            sum += (fMap.get(index - 4 - i) % flag);
            sum = sum % flag;
        }
        //L开头，┐结尾
        return sum;
    }
}