基本原理
数学推导
最小二乘法是通过输入数据与输出数据来拟合已知结构的函数关系,也就是说已知二者的函数关系,通过最小二乘法估计函数的相关参数。假设
x
,
y
x,y
x,y存在以下函数关系:
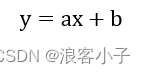
但是在实际中,测量数据时存在测量误差或者噪声影响,故而实际的函数关系为
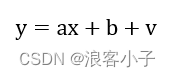
v
v
v表示测量误差,这是一个小范围内的随机值。将所有测量误差相加
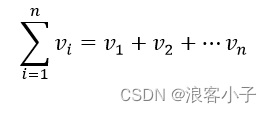
我们以测量误差的平方和最小代表测量总误差最小,即
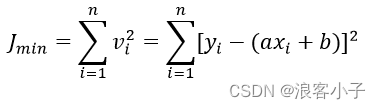
用求极值的方法使
J
J
J对
a
,
b
a,b
a,b求一阶导并等于
0
0
0:
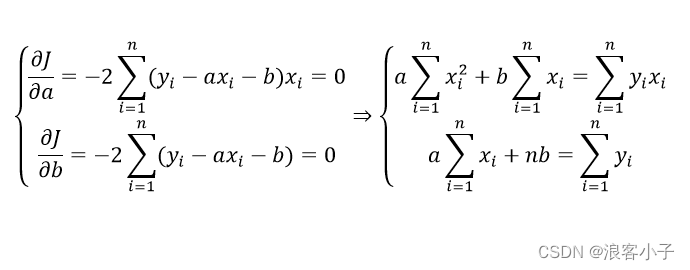
解方程组得
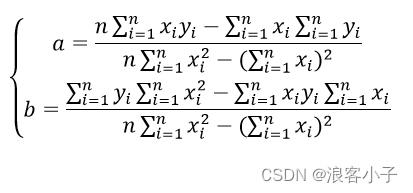
实例验证
某函数为

计算
12
12
12组值如下表所示:
| x | 10 | 21 | 33 | 54 | 66 | 68 | 90 | 100 | 121 | 133 | 150 | 181 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| y | 46.2 | 72 | 120.6 | 179.5 | 215.4 | 229.3 | 275.7 | 317.8 | 384.9 | 419.1 | 467.2 | 558.9 |
以下为 m a t l a b matlab matlab程序:
clear all
close all
clc
x=[10,21,33,54,66,68,90,100,121,133,150,181];
y=[46.2,72,120.6,179.5,215.4,229.3,275.7,317.8,384.9,419.1,467.2,558.9];
n=12;
S_x=0;
S_y=0;
S_xy=0;
S_xx=0;
for i=1:n
S_x=S_x+x(i);
S_y=S_y+y(i);
S_xy=S_xy+x(i)*y(i);
S_xx=S_xx+x(i)*x(i);
end
b=(S_y*S_xx-S_xy*S_x)/(n*S_xx-S_x*S_x)
a=(n*S_xy-S_x*S_y)/(n*S_xx-S_x*S_x)
%最小二乘拟合
A=polyfit(x,y,1);
z=polyval(A,x);
%画图
figure
plot(x,y,'b+')
figure
plot(x,z);
figure
plot(x,y,'b+')
hold on
plot(x,z,'r');
hold off
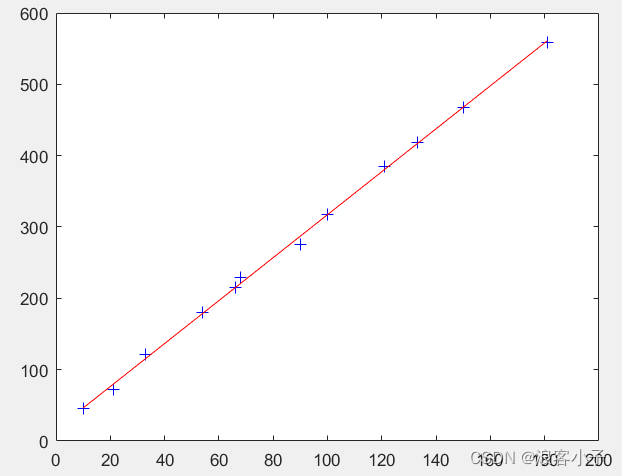
最终计算得
a
,
b
a,b
a,b值为

可见其与原函数参数很相近了,参数辨识较为理想,拟合曲线如下
一般最小二乘法
对于
s
i
s
o
siso
siso系统,其模型如下:
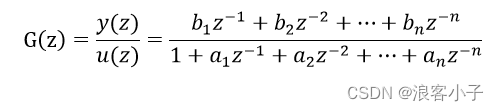
转换成差分方程形式
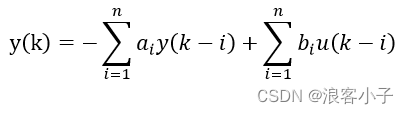
考虑到测量噪声存在,故而实际差分方程为
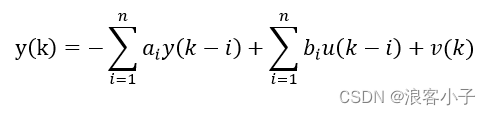
令
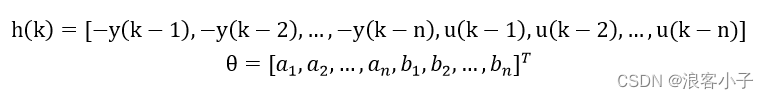
则可将原系统改写成

其中,
k
=
1
,
2
,
3...
n
k=1,2,3...n
k=1,2,3...n,则有
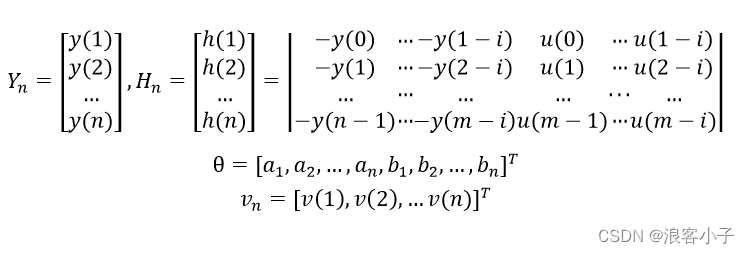
写成矩阵形式
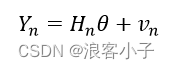
同理,使测量误差的平方和最小
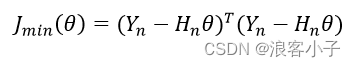
根据极值定理,得
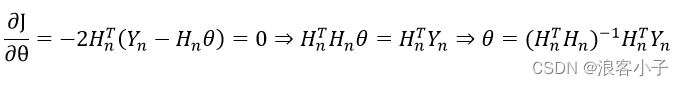
这种方法进行系统辨识是可行的,但并不一定满足使用要求,因为这种方法需要全部的数据,也就是说先采集数据然后再估计参数,不仅不能实时估计,还占用大量的存储空间,故而仍需进一步改善。
递推最小二乘法
递推最小二乘法的思想就是用上一次的估计值加上修正项得到当前估计值,这样就可以实时得到参数估计值。设
k
k
k时刻的参数估计为
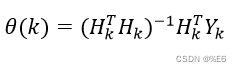
式中
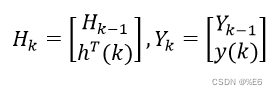
令
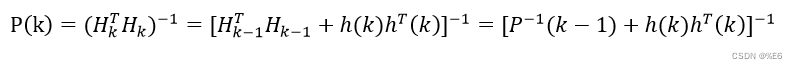
得
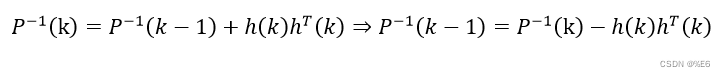
那么
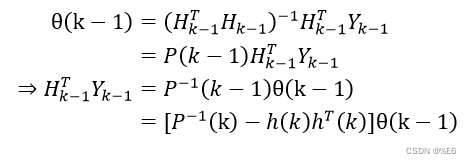
故而第
k
k
k时刻的最小二乘估计为
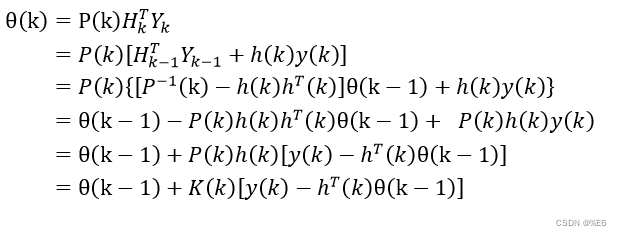
其中
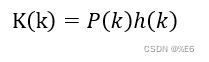
前面提到式子
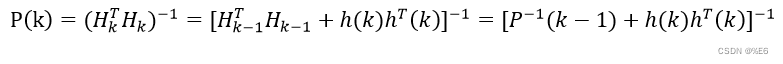
由矩阵求逆公式
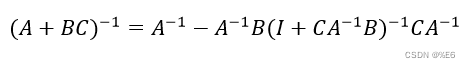
得
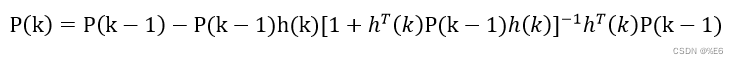
于是归纳
K
(
k
)
K(k)
K(k)得
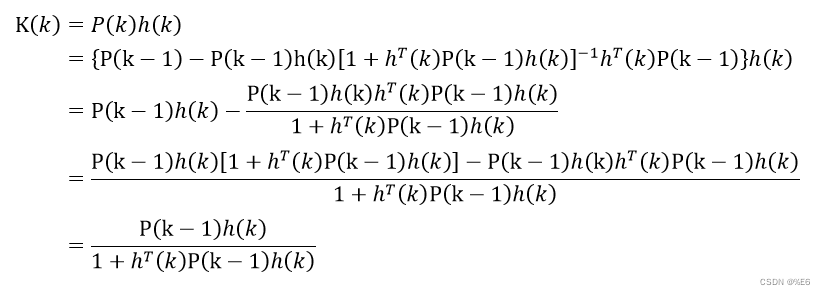
再次归纳
P
(
k
)
P(k)
P(k)得
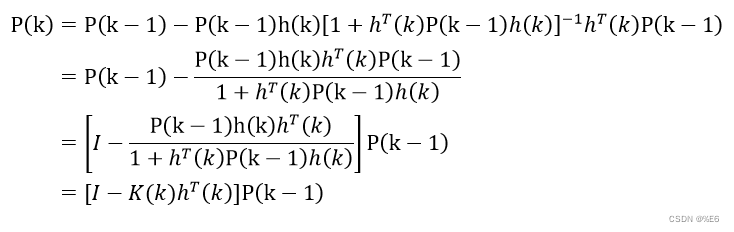
最终得到递推最小二乘法公式为
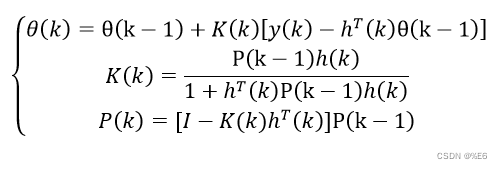
式中
I
I
I表示单位矩阵,且令
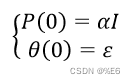
其中
α
α
α为一个较大的正实数
(
1
0
4
−
1
0
9
)
(10^4 -10^9)
(104−109),
ε
ε
ε为一个充分小的正实数或向量
(
ε
<
0.01
)
(ε<0.01)
(ε<0.01)。
实例验证
已知有系统模型为
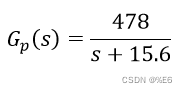
取采样周期为
T
s
=
0.01
s
Ts=0.01s
Ts=0.01s,将该模型离散化
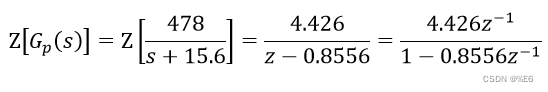
s
i
n
m
u
l
i
n
k
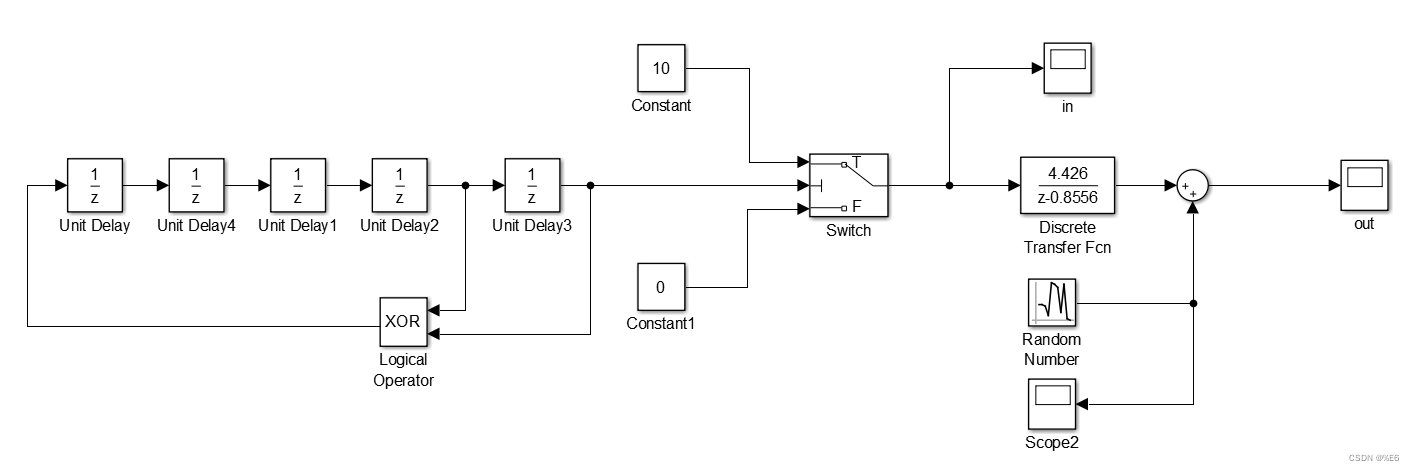
sinmulink
sinmulink中采集数据,如下图
m
a
t
l
a
b
matlab
matlab代码如下
L=length(in);
c0=[0.001 0.001]';
p0=1000*eye(2,2);
for k=2:L;
h1=[out(k-1),in(k-1)]';
k1=p0*h1*inv(h1'*p0*h1+1);
new=out(k)-h1'*c0;
c1=c0+k1*new;
p1=(eye(2)-k1*h1')*p0;
c0=c1;
p0=p1;
end
c1
得结果为

即
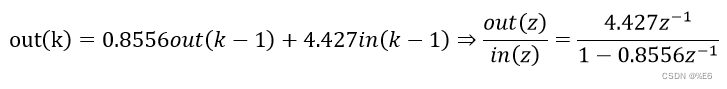
可见参数与原系统相差无几,精度较为理想。