数组与广义表

文章目录

数组与广义表
数组
- 数组的基本概念
- 性质
- 数组的存储结构
- - 一维数组的存储结构
  - 二维数组的存储结构
特殊矩阵的压缩存储
- 对称矩阵
- 上三角矩阵
- 下三角矩阵
- 对角矩阵
稀疏矩阵
- 定义
- 稀疏矩阵的三元组表示
- 稀疏矩阵的存储结构及其基本运算算法
- - 定义
  - 存入三元组
  - 三元组元素赋值
  - 取元素
  - 输出三元组
- 十字链表法
- - 定义
广义表
- 定义
- 广义表的重要概念
- 广义表的存储结构
- - 广义表的结点定义
- 广义表算法设计方法
- 求广义表的长度
- 求广义表的深度
- 输出广义表
- 建立广义表的链式存储结构
- 销毁广义表
- main函数测试
广义表例题--求原子个数

数组

数组的基本概念

在这里插入图片描述

性质

数组中的数据元素数目固定。一旦定义了一个数组，其数据元素数目不再有增减的变化。
数组中的数据元素具有相同的数据类型。
数组中的每个数据元素都和一组唯一的下标对应。
数组是一种随机存储结构。可随机存取数组中的任意数据元素。

注意

考研数据结构中的数组是作为一种数据结构讨论的。
而编程语言中的数组是一种数据类型。
前者可以借助后者来存储，像线性表的顺序存储结构即顺序表就是借助一维数组这种数据类型来存储的。但两者不能混淆。

数组的存储结构

数组特别适合采用顺序存储结构->将数组所有元素存储在一块地址连续的内存单元中。

数组不能采用链式存储结构吗？

答：数组可以采用链式存储结构，但是不常见。链式存储结构是用一组任意的存储单元存储线性表的数据元素，每个元素包括数据域和指针域。数组的数据域可以存储在链表的节点中，指针域可以指向下一个数组元素的位置。这样的链式存储结构称为静态链表，它是用一片连续的空间（数组，顺序）来存储实现的。

为什么数组一般采用顺序存储结构？

答：数组一般采用顺序存储结构，因为这样可以利用数组的随机访问特性，通过索引快速找到对应元素，而且相对节约存储空间。顺序存储结构就是把线性表中的所有元素按照某种逻辑顺序，依次存储到从指定位置开始的一块连续的存储空间。如果数组采用链式存储结构，就无法根据一个索引算出对应元素的地址，所以不能随机访问；而且由于每个元素必须存储指向前后元素位置的指针，会消耗相对更多的储存空间。

一维数组的存储结构

在这里插入图片描述

二维数组的存储结构

以行序为主

在这里插入图片描述

若首元素是a00(此时尾元素是n-1),那么LOC(ai,j)=LOC(a00)+[ixn+j]xk

以列序为主

在这里插入图片描述

特殊矩阵的压缩存储

特殊矩阵是指非零元素或零元素的分布有一定规律的矩阵。

为了节省存储空间，特别是当高阶矩阵的情况下，可以利用特殊矩阵的压缩存储来提高存储空间效率。

特殊矩阵的主要形式有:

(1)对称矩阵

(2)上三角矩阵/下三角矩阵

(3)对角矩阵

它们都是方阵，即行数和列数相同。

对称矩阵

在这里插入图片描述

上三角矩阵

在这里插入图片描述

下三角矩阵

在这里插入图片描述

对角矩阵

在这里插入图片描述

以三对角矩阵为例

在这里插入图片描述

稀疏矩阵

定义

一个阶数较大的矩阵中的非零元素个数s相对于矩阵元素的总个数t十分小时，即s<<t时，称该矩阵为稀疏矩阵。

因子&=s/t<=0.05

例如一个100×100的矩阵，若其中只有100个非零元素，就可称其为稀疏矩阵。

疏矩阵和特殊矩阵的不同点:

特殊矩阵的特殊元素(值相同元素、常量元素)分布有规律。
稀疏矩阵的特殊元素（非0元素）分布没有规律。

稀疏矩阵的三元组表示

在这里插入图片描述

稀疏矩阵的存储结构及其基本运算算法

在这里插入图片描述

定义

把稀疏矩阵的三元组线性表按顺序存储结构存储，则称为稀疏矩阵的三元组顺序表。

// 定义最大容量为100
#define MaxSize 100

// 定义稀疏矩阵的三元组结构体
typedef struct {
    int r; // 非零元素的行下标
    int c; // 非零元素的列下标
    int d; // 非零元素的值
} TupNode;

// 定义稀疏矩阵的结构体
typedef struct {
    int rows; // 矩阵的行数
    int cols; // 矩阵的列数
    int nums; // 非零元素的个数
    TupNode data[MaxSize]; // 三元组表
} TSMatrix;

在这里插入图片描述

约定: data域中表示的非零元素通常以行序为主序顺序排列，它是一种下标按行有序的存储结构。

这种有序存储结构可简化大多数矩阵运算算法。

存入三元组

在这里插入图片描述

// 将二维矩阵A转换为稀疏矩阵t
void CreatMat(TSMatrix &t, int A[M][N]) {
    t.rows = M; // 稀疏矩阵的行数为A的行数
    t.cols = N; // 稀疏矩阵的列数为A的列数
    t.nums = 0; // 稀疏矩阵的非零元素个数初始化为0
    for (int i = 0; i < M; ++i) { // 遍历A的每一行
        for (int j = 0; j < N; ++j) { // 遍历A的每一列
            if (A[i][j] != 0) { // 如果A[i][j]不为0
                t.data[t.nums].r = i; // 将其行下标存入稀疏矩阵的三元组
                t.data[t.nums].c = j; // 将其列下标存入稀疏矩阵的三元组
                t.data[t.nums].d = A[i][j]; // 将其值存入稀疏矩阵的三元组
                t.nums++; // 稀疏矩阵的非零元素个数加1
            }
        }
    }
}

三元组元素赋值

在这里插入图片描述

// 在稀疏矩阵t中插入元素x，行下标为i，列下标为j
bool Value(TSMatrix &t, int x, int i, int j) {
    int k = 0, k1; // 定义k和k1
    if (i >= t.rows || j >= t.cols) return false; // 如果i大于等于t的行数或j大于等于t的列数，返回false
    while (k < t.nums && i > t.data[k].r) k++; // 找到第一个行下标大于等于i的元素
    while (k < t.nums && i == t.data[k].r && j > t.data[k].c) k++; // 找到第一个行下标等于i且列下标大于等于j的元素
    if (i == t.data[k].r && j == t.data[k].c) { // 如果找到了行下标为i，列下标为j的元素
        t.data[k].d = x; // 将其值改为x
    } else { // 如果没有找到行下标为i，列下标为j的元素
        for (k1 = t.nums - 1; k1 >= k; k1--) { // 从后往前遍历，将第k个元素及其后面的元素后移一位
            t.data[k1 + 1].r = t.data[k1].r;
            t.data[k1 + 1].c = t.data[k1].c;
            t.data[k1 + 1].d = t.data[k1].d;
        }
        t.data[k].r = i; // 将新元素的行下标存入第k个元素的位置
        t.data[k].c = j; // 将新元素的列下标存入第k个元素的位置
        t.data[k].d = x; // 将新元素的值存入第k个元素的位置
        t.nums++; // 稀疏矩阵的非零元素个数加1
    }
    return true; // 返回true
}

取元素

在这里插入图片描述

// 在稀疏矩阵t中查找元素，行下标为i，列下标为j，将其值存入x中
bool Assign(TSMatrix t, int &x, int i, int j){
    int k = 0; // 定义k
    if (i >= t.rows || j >= t.cols) return false; // 如果i大于等于t的行数或j大于等于t的列数，返回false
    while (k < t.nums && i > t.data[k].r) k++; // 找到第一个行下标大于等于i的元素
    while (k < t.nums && i == t.data[k].r && j > t.data[k].c) k++; // 找到第一个行下标等于i且列下标大于等于j的元素
    if (i == t.data[k].r && j == t.data[k].c) { // 如果找到了行下标为i，列下标为j的元素
        x = t.data[k].d; // 将其值存入x中
    } else { // 如果没有找到行下标为i，列下标为j的元素
        x = 0; // 将x赋值为0
    }
    return true; // 返回true
}

输出三元组

// 输出稀疏矩阵t的三元组表
void DispMat(TSMatrix t){
    if (t.nums<=0)return; // 如果稀疏矩阵的非零元素个数为0，直接返回
    printf("\t%d\t%d\t%d\n",t.rows,t.cols,t.nums); // 输出稀疏矩阵的行数、列数和非零元素个数
    printf("-------------------------------\n"); // 输出分隔线
    for (int i = 0; i < t.nums; ++i) { // 遍历稀疏矩阵的每一个非零元素
        printf("\t%d\t%d\t%d\n",t.data[i].r,t.data[i].c,t.data[i].d); // 输出该元素的行下标、列下标和值
    }
}

十字链表法

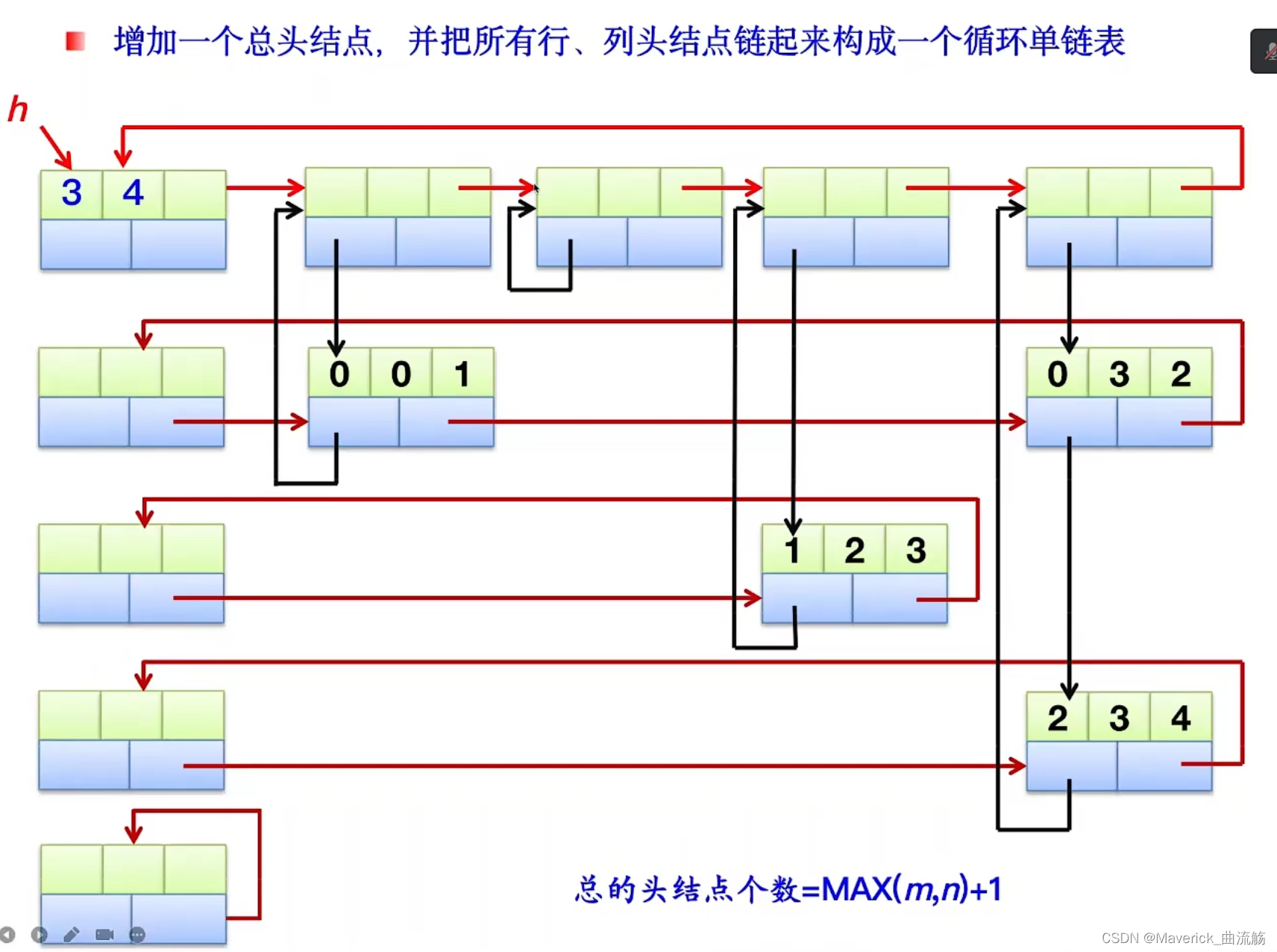
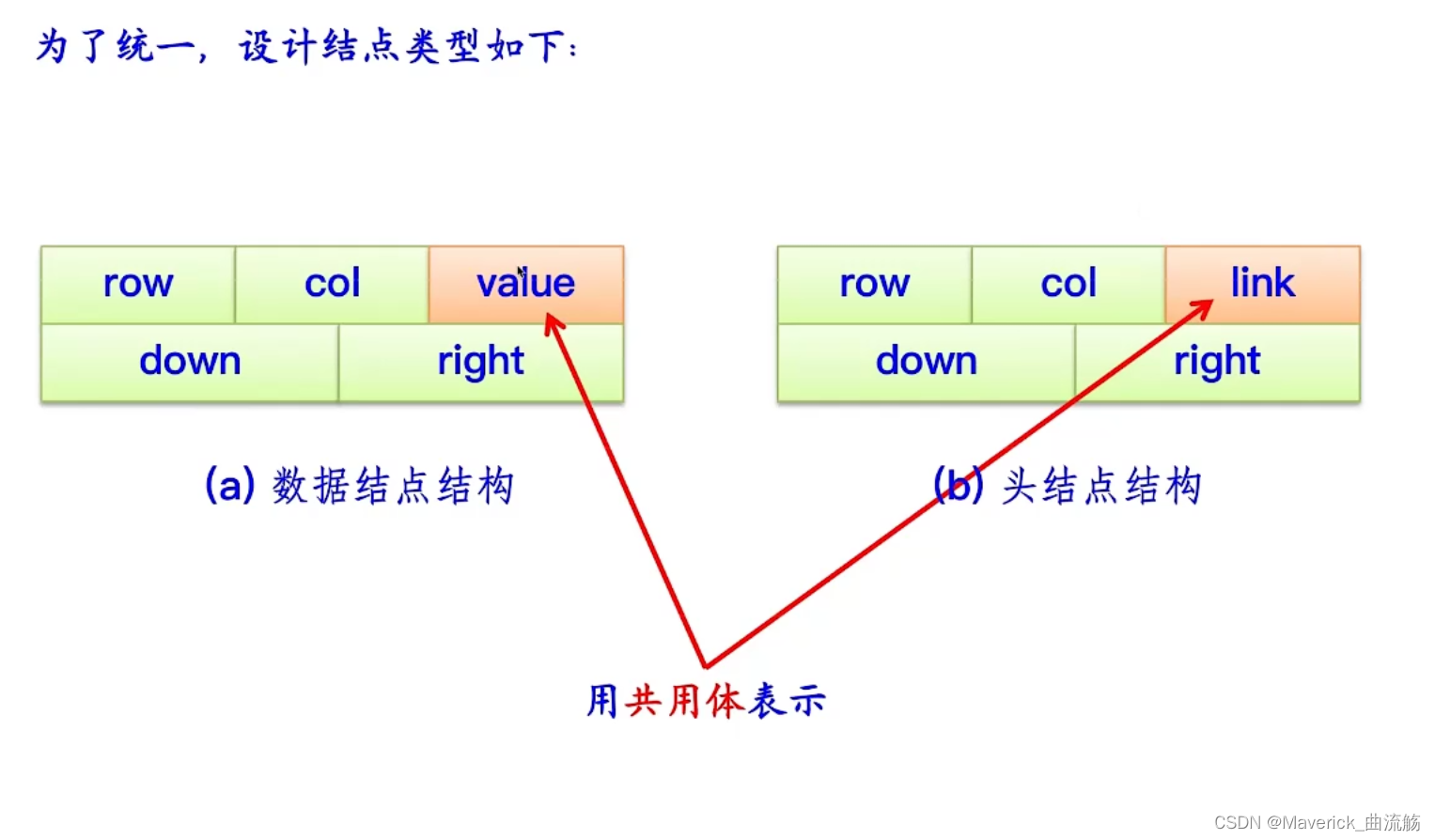
在这里插入图片描述

定义

// 定义常量M和N
#define M 3
#define N 2

// 定义常量Max，表示M和N中的最大值
#define Max ((M)>(N)?(M):(N))

// 定义结构体MatNode，表示稀疏矩阵的节点
typedef struct mtxn{
    int row; // 行下标
    int col; // 列下标
    struct mtxn *right,*down; // 指向右边和下面的节点
    union {
        int value; // 节点的值
        struct mtxn *link; // 指向另一个节点的指针
    } tag;
} MatNode;

广义表

定义

广义表的定义：广义表是线性表的推广，它是由零个或多个原子或子表组成的有限序列。
广义表可以用递归方法定义为：
- 广义表是由原子和广义表组成的列表；
- 原子是不可再分的数据单位；
- 列表是由零个或多个原子或广义表组成的有限序列。

广义表通常用圆括号括起来表示，例如：(a,b,c)是一个由三个原子组成的广义表；(a,(b,c),d)是一个由两个原子和一个子表组成的广义表。

在这里插入图片描述

广义表的重要概念

在这里插入图片描述

广义表的存储结构

在这里插入图片描述

广义表的结点定义

typedef struct Inode{
    int tag; // 标记，用于区分是数据还是子表
    union {
        int data; // 数据域
        struct Inode *sublist; // 子表指针
    } val; // 共用体，用于存储数据或子表指针
    struct Inode *link; // 指向下一个节点的指针
} GLNode;

广义表算法设计方法

在这里插入图片描述

求广义表的长度

// 计算广义表的长度
int GLLength(GList g){
    if (g == NULL){ // 如果当前节点为空
        return 0; // 返回 0
    }
    return 1 + GLLength(g->link); // 递归计算下一个节点的长度
}

在这里插入图片描述

求广义表的深度

int GLDepth2(GList g){
    GList g1; // 用于遍历所有子表的指针
    int maxDep = 0; // 储存最大深度值
    int dep; // 储存当前深度值
    if (g->tag == 0) return 0; // 如果为原子结点，返回 0，即深度为 0
    g1 = g->val.sublist; // 指针 g1 指向 g 的子表
    if (g1 == NULL) return 1; // 如果子表为空，返回 1，即深度为 1
    while (g1 != NULL){ // 遍历所有子表
        if (g1->tag == 1){ // 如果该子表非空
            dep = GLDepth2(g1); // 递归计算深度值
            if (dep > maxDep) maxDep = dep; // 更新最大深度值
        }
        g1 = g1->link; // 指针 g1 移动到下一个节点
    }
    return maxDep+1; // 返回最大深度加上当前节点的深度（即 1）
}

在这里插入图片描述

输出广义表

在这里插入图片描述

// 定义一个函数，用于输出打印广义表
void PrintGL(GList g){
    if (g == NULL){ // 如果当前广义表为空表
        printf("#"); // 输出井号
    } else if (g->tag == 0){ // 如果当前元素是原子
        printf("%c", g->val.data); // 输出原子的值
    } else{ // 如果当前元素是子表
        printf("("); // 输出左括号
        PrintGL(g->val.sublist); // 递归打印子表
        printf(")"); // 输出右括号
    }
    if (g != NULL && g->link != NULL){ // 如果当前元素不是最后一个元素
        printf(","); // 输出逗号
        PrintGL(g->link); // 递归打印下一个元素
    }
}

// 定义一个函数，用于输出打印广义表
void DispGL(GList g){
    if (g != NULL){ // 如果当前节点不为空
        if (g->tag == 0){ // 如果当前节点是原子节点
            printf("%c", g->val.data); // 输出当前节点的值
        } else{ // 如果当前节点是子表节点
            printf("("); // 输出左括号
            if (g->val.sublist == NULL){ // 如果子表为空
                printf("#"); // 输出 #
            } else{ // 如果子表不为空
                DispGL(g->val.sublist); // 递归打印子表
            }
            printf(")"); // 输出右括号
        }
        if (g->link != NULL){ // 如果当前元素不是最后一个元素
            printf(","); // 输出逗号
            DispGL(g->link); // 递归打印下一个元素
        }
    }
}

在这里插入图片描述

建立广义表的链式存储结构

在这里插入图片描述

// 创建广义表
GList CreateGL(char *&s){
    GList g; // 定义一个广义表
    char ch = *s++; // 取出当前字符
    if (ch !='\0'){ // 如果当前字符不是结束符
        g = (GLNode *) malloc(sizeof(GLNode)); // 分配内存
        if (ch == '('){ // 如果当前字符是左括号
            g->tag = 1; // 标记为子表
            g->val.sublist = CreateGL(s); // 递归创建子表
        } else if (ch == '#'){ // 如果当前字符是井号
            g = NULL; // 标记为空表
        } else{ // 如果当前字符是其他字符
            g->tag = 0; // 标记为原子
            g->val.data = ch; // 存储原子的值
        }
    } else{ // 如果当前字符是结束符
        g = NULL; // 标记为空表
    }
    ch = *s++; // 取出下一个字符
    if (g != NULL){ // 如果当前广义表不为空表
        if (ch == ','){ // 如果下一个字符是逗号
            g->link = CreateGL(s); // 递归创建下一个元素
        } else{ // 如果下一个字符不是逗号
            g->link = NULL; // 标记为最后一个元素
        }
    }
    return g; // 返回创建好的广义表
}

// 创建广义表
GList CreateGL2(char *&s){
    GList g; // 定义一个指向广义表的指针
    char ch = *s++; // 获取字符串中的下一个字符
    switch (ch) {
        case '(':
            g = (GLNode *) malloc(sizeof(GLNode)); // 分配内存以存储广义表节点
            g->tag = 1; // 设置节点标记为1，表示这是一个子列表
            g->val.sublist = CreateGL(s); // 递归调用CreateGL函数来创建子列表
            break;
        case '#':
            g = NULL; // 如果字符是#，则表示这是一个空列表，将指针设置为NULL
            break;
        default:
            g = (GLNode *) malloc(sizeof(GLNode)); // 分配内存以存储广义表节点
            g->tag = 0; // 设置节点标记为0，表示这是一个原子
            g->val.data = ch; // 将字符转换为整数并将其存储在节点中
            break;
    }
    if (g == NULL || *s == '\0') { // 如果指针为NULL或字符串已经结束，则返回指针
        g->link = NULL;
        return g;
    }
    g->link = CreateGL(s); // 递归调用CreateGL函数来创建广义表的下一个节点
    return g;
}

在这里插入图片描述

图解

在这里插入图片描述

销毁广义表

void DestroyGL(GList g){
    if (g != NULL){ // 如果当前节点不为空
        if (g->tag == 1){ // 如果当前节点是子表节点
            DestroyGL(g->val.sublist); // 递归销毁子表
        }
        DestroyGL(g->link); // 递归销毁下一个元素
        free(g); // 释放当前节点的内存
    }
}

在这里插入图片描述

main函数测试

int main(){
    char *s = "(a,b,(c,d),e,(#))";
    char *s2 = "(a,b,(c,d),e)";
    GList g = CreateGL(s);
    GList g2 = CreateGL2(s2);
    PrintGL(g);
    PrintGL(g2);
    printf("销毁广义表");
    DestroyGL(g);
    return 0;
}