1.如何理解卷积？
t时刻的输出信号是t时刻之前的无数小的脉冲序列冲击引起的。
2. 如何理解欧拉公式，复指数信号呢？

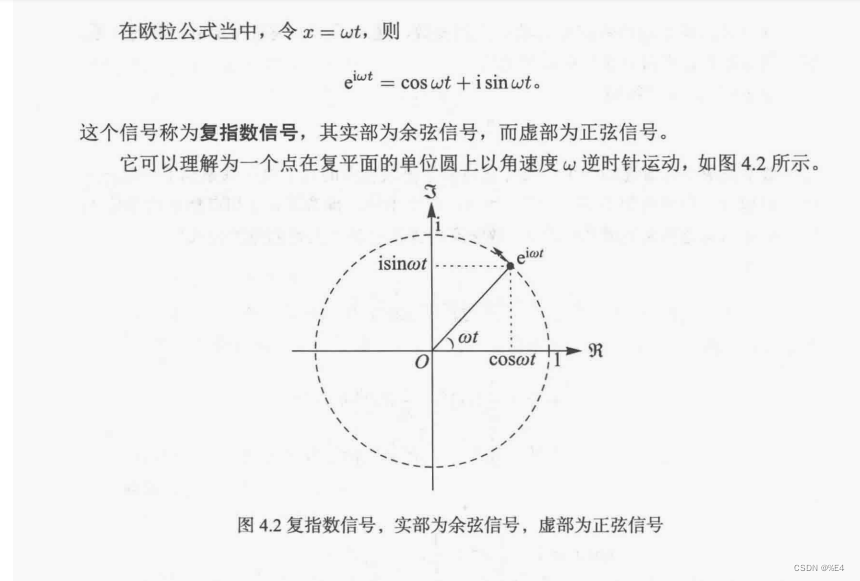
可以看成一个点在复平面上以角速度w进行逆时针的旋转。
傅里叶分析：
整体到部分，把一个信号分解成无数个基频组成的信号的和的过程。
ofdm就用到了傅里叶分析实现，但是ofdm并不是信号分析，只是傅里叶变换的一个应用，因为ofdm中的
基频是确定的。

3. 如何理解负频率？
负频率在物理世界中是不存在的，但是在研究信号的时候有用吗？
有的，因为信号在调制的时候，实际上是对信号频谱的一个搬移的过程，比如说载波频率为Wc，基带信号经过傅里叶变换之后
的频率只有±w1，那么搬移之后的频谱是Wc±w1. Wc>>w1, 但是正负频率承载的信息实际是一样的，这样就造成了频谱的浪费。

4.如何理解离散傅里叶变换？离散信号的连续傅里叶变换？以及连续信号的连续傅里叶变换？
最容易理解的就是连续信号的连续傅里叶变换，这个是初次学习傅里叶分析的时候的公式表示的内容，即信号是一个时间t的函数，而傅里叶变换的正交频率空间也是关于t的函数，即e^{-jwt}
首先将2Π的弧度进行离散化，那么这样的基频率就构成了一组正交基。
信号也是离散的，离散傅里叶变换就是求这个信号在这个正交基上的坐标。
离散傅里叶反变化就是利用正交基合成这个离散的信号。

5.如何理解奈奎斯特采样定理？
从频谱搬移的角度理解，因为采样之后相当于对基带信号的频谱搬移到了采样频率上去。
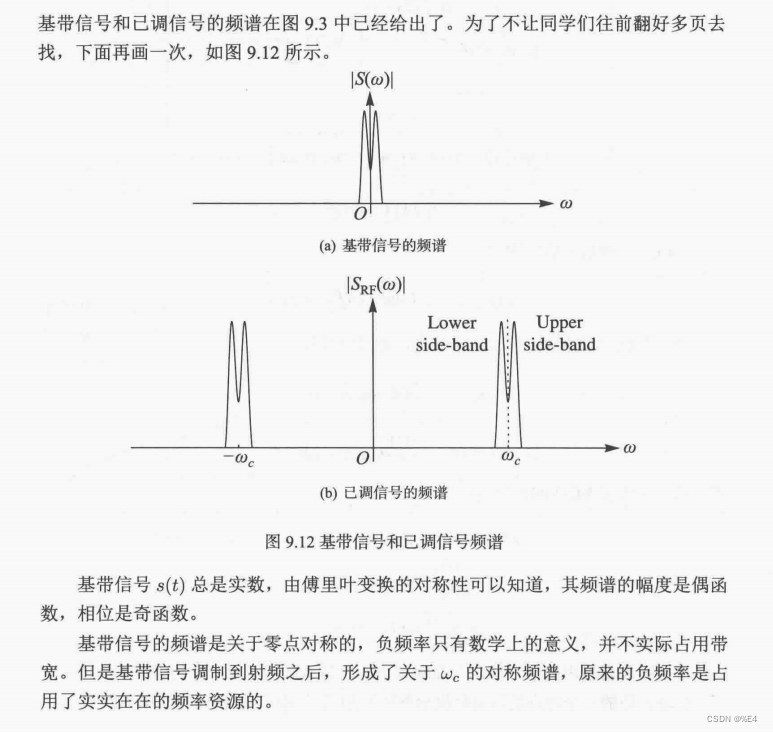
频谱搬移之后，正负频率就都存在了，回忆下，基带信号的频谱是关于中心0处的频率对称的。

6.从线性空间角度理解傅里叶变换以及傅里叶级数的展开。
正变换就是求一个信号在一组正交的频率空间上的系数，反变换则是利用这个正交的频率空间合成所需要的信号。

7.浅谈一下为什么引入IQ调制？
从频带利用率到希尔伯特变换再到IQ调制。是什么以及为什么要用？要用它肯定是因为它简单并且可以解决我们想要解决的问题啊。
希尔伯特变换与单边带信号
回忆下，基带信号调制之后，频谱发生了搬移，正负频率在载频处都出现了，但是时候下边带信号（也就是载频的左边的信号）和右边的信号占据的带宽是一样的，并且二者携带了相同的信息。实际上是对频谱资源的浪费。
那怎么更加合理的利用频谱资源呢？当然是只保留一半的频谱了。这时候就要对调制信号的频谱滤除一半部分的带宽就ok了。
所以我需要在频域设计一个滤波函数，滤除一半的频谱，保留单边带的信号。

8. 请解释一下这个公式9.6表达的含义。
基地啊脉冲成型函数以及复基带函数的表示。

这个公式的意思是将时间t轴分成无数的小段，每一个映射之后的符号(对应一个星座点，就是一个复数值)都被在一个Ts周期内传输，Ts就是传输一个星座点的时间。每一个星座点都被g()函数调制，把g()函数在时间轴上的波形叠加起来，就得到了脉冲成型之后的时域信号的波形，即s(t).哈哈哈哈，我自己翻译的似乎不是很好，贴一下，专业的翻译：

安利《通信之道》这本书！！