Java中进制基础知识与算法题

本篇文章旨在给大家普及下计算机内部数据的机器级表示方式，即：二进制、八进制、十进制、十六进制…

对于进制，我们从小最先接触的是十进制，这个也是我们日常生活中应用最多的数值统计方式。然而，现实中我们感觉到的媒体信息(如图文、音频、动画等)，在计算机世界里，它们又是怎么表现的呢？也是1,2,3,4…这样表示？

显然，是不可能的。你可能会问为什么呢？在计算机中所有信息都采用二进制编码表示，因为机器处理指令的硬件都是双态的，只要是涉及到数据的，就用电位的 “高” 或 “低”表示，即二进制的 “1” 或 “0”，这样就方便通过逻辑运算电路来实现算术运算了。

但是对于我们程序员来编写程序，需要考虑这些进制转换吗？可以负责任的说，不需要的。因为，我们开发中是使用的高级程序设计语言，即：较为接近日常所用的英语书面语言的程序设计语言。它能成为可执行的机器语言之前，是需要经过编译成二进制才能执行的。

这里的文章主要是为了让大家了解数据在计算中存储与网络传输中表示形式，和应付一些面试题。

进制知识体系：

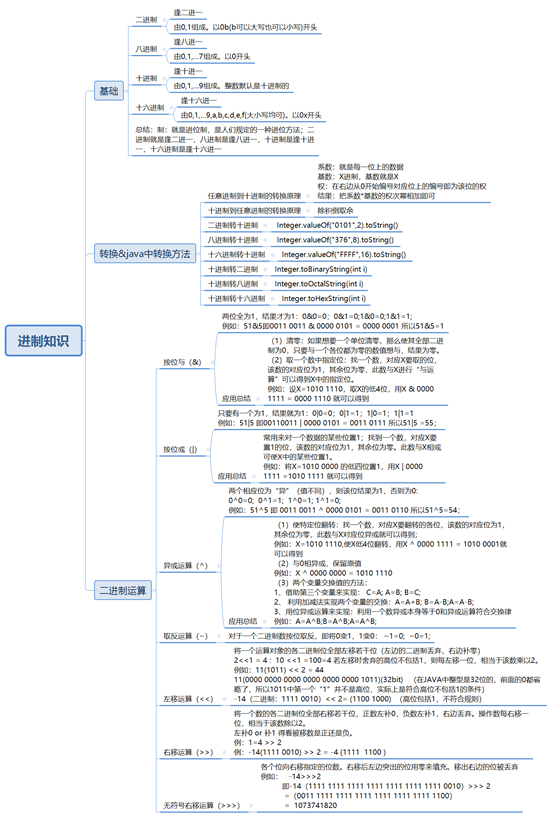
进制表：

十进制	二进制	八进制	十六进制
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
…	…	…	…
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
…	…	…	…
15	1111	17	F
16	10000	20	10
17	10001	21	11
18	10010	22	12
…	…	…	…

二进制知识补充：

计算机中的数据都以二进制数字保存。

二进制：逢二进一。即只有 0、1 两个值。如：十进制的 10 在计算机内保存为二进制的 1010。

计算机中信息的存储单位：

位(Bit)：表示一个二进制数码 0 或 1，是计算机存储处理信息的最基本的单位。

字节(Byte)：一个字节由 8 个位组成。它表示作为一个完整处理单位的 8 个二进制数码。

事实上，计算机内的二进制数值是以补码形式表示的。

一个正数的补码和其原码的形式是相同的。

负数的补码是：将该数的绝对值的二进制形式，按位取反再加 1。

由此可知，二进制补码数值的最高位(最左位)是符号位：该位为 0，表示数值为正数；该位为 1，表示数值为负数。

10=	00000000 00000000 00000000 00001010
-10=	11111111 11111111 11111111 11110110

主要原因：使用补码，可以将符号位和其它位统一处理；同时，减法也可按加法来处理。另外，两个用补码表示的数相加时，如果最高位(符号位)有进位，则进位被舍弃。

负数以其正值的补码形式表示：

原码：一个整数按照绝对值大小转化成的二进制数为原码

例如：14的原码为0000 0000 0000 0000 0000 0000 0000 1110

反码：将二进制数按位取反，所得的新二进制数称为原二进制数的反码。

例如：14的反码为1111 1111 1111 1111 1111 1111 1111 0001

补码：反码加1称为补码

例如：1111 1111 1111 1111 1111 1111 11110001 +1 = 1111 1111 1111 1111 1111 1111 11110010

-14(1111 1111 1111 1111 1111 1111 1111 0010)<< 2

=(1111 1111 1111 1111 1111 1111 1100 1000)

=？(即为-56)

分析：只需要求出该补码的原码对应的正值，然后取相反数：

1、补码减一得到反码：(...1100 0111)

2、补码取反得到原码(即该负数的正值) (...0011 1000)

3、计算正值按照二-十进制转换规则，正值为56

4、取相反数就会得到负数：-56

算法题一：数字机制处理

反馈机制：

(1)接收字符串s不包含连续1，返回s

(2)否则，返回一个大于s对应二进制数字，且不包含连续1的最小二进制。

根据此机制返回结果。

例子1：

输入：s=”101010”，输出：”101010”

例子2：

输入：s=”100011”，输出：”100100”

例子3：

输入：s=”110011”，输出：”1000000”

提示：s.length =[1, 10^5]

解题思路：

1)递归处理

2)出现”11”，那么大于11二进制计算:11+01=100，则该值可以按照规则处理成100

 1     public String getSResult(String s) {
 2         if(!s.contains("11")) {
 3             return s;
 4         } else {
 5             StringBuilder sb = new StringBuilder();
 6             int idx = s.indexOf("11");
 7             if(idx > 0) {
 8                 sb.append(s.substring(0, idx - 1));
 9             }
10             sb.append("1");
11             for (int i=0; i<s.length()-idx; i++) {
12                 sb.append("0");
13             }
14             return getSResult(sb.toString());
15         }
16     }

总结说明：这里使用到字符串快速拼接StringBuild，如果可以确定拼接长度的话，建议创建的时候就初始化好空间，减少频繁扩容操作。

算法题二：校验和

内容中每个字节用2位十六进制数字表达，处理规则如下：

(1) 待校验和字节长度不是4的倍数，就在尾部加0xFF字节补齐成4的倍数，最多可加3字节；

(2) 若补齐后是4的倍数，那么除以4得到一个正整数n

1)n=1,那么补齐后的校验和就是结果(16进制)

2)n>1,先取开头4字节与第5~8字节进行异或运算，然后得到的结果再与随后4字节进行异或运算，直到最后，得到的结果就是校验和(16进制4字节)。

例子1：

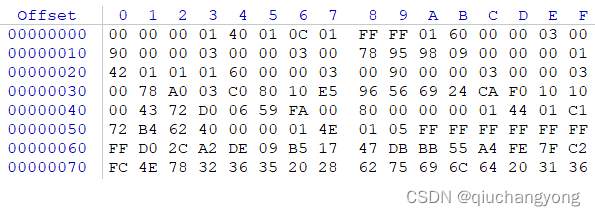
输入：43 66 53 74 34 39 42 2A 21 AC 11

输出：56F300A1

说明：1)输入报文长度是11，那么补齐4的倍数为43 66 53 74 34 39 42 2A 21 AC 11 FF，倍数n=3 >1

2)每次取4个字节，第一个0x43665374，与第二个0x3439422A，异或运算结果为0x775f115e，再与第三个0x21AC11FF异或运算结果为0x56F300A1，那么最终输出结果为56F300A1。

例子2：

输入：32

输出：32FFFFFF

说明：1)输入报文长度是1，那么补齐4的倍数为32 FF FF FF，倍数n=1==1，那么得到的校验和即为32FFFFFF。

解题思路：

1)考点是16进制异或运算

2)每4个字节进行异或运算，注意数值前面要加0x表示16进制。

 1     public static void getResult(String s) {
 2         int len = s.length();
 3         int n = len % 8 == 0 ? len >> 3 : (len >> 3) + 1;
 4         String resTmp = StringUtils.rightPad(s, n<<3, "F");
 5         if (n == 1) {
 6             System.out.println(resTmp);
 7         } else {
 8             String tmp = resTmp.substring(0, 8);
 9             for (int i=1; i< n; i++) {
10                 int idx = i << 3;
11                 tmp = Integer.toHexString(Integer.valueOf(tmp,16) ^ Integer.valueOf(resTmp.substring(idx, idx+8),16));
12             }
13             System.out.println(StringUtils.leftPad(tmp, 8, "0").toUpperCase());
14         }
15     }

总结说明：

(1) 这里使用到>>移位操作符，其实>>3意义就是除以8，每移一位就是2的次幂。含义可详见前面进制知识。总结说明：

(2) 还用到或运算^和java中进制相互转换的方法。

(3)字符串左补齐leftPad或者右补齐rightPad方法，再JDK中是不存在，需要添加相应的jar包才可以实现，当然，也可以自己实现方法。

算法题三：编码格式处理

题目大概意思是这样的，一个特殊的编码格式，各字节按照以下规则：

1)单字节(n=1)，字节第一位0，其余为有效位

2)多字节(n>1且n<=6)，第一个字节前n位都为1，第n+1位为0；后面每个字节前2位都为10，其余是有效位。

二进制规则格式如下：

N=1：0xxxxxxx

N=2：110xxxxx 10xxxxxx

N=3：1110xxxx 10xxxxxx 10xxxxxx

…

N=6：1111110x 10xxxxxx 10xxxxxx 10xxxxxx 10xxxxxx 10xxxxxx

其中x表示有效位，从左边开始将所有字节有效位拼接，形成的十进制为结果。

若合法，返回该字符的结果；否则，返回-1。

例子1：

输入：F1B180A5

输出：462885

说明：1)输入长度为n=3，第一字节E9为11101001，第二个字节80为10000000，第三个字节A5为10100101。

那么二进制表示：11110001 10110001 10000000 10100101

有效位拼接为：1001 000000 100101 ，那么十进制为462885。

例子2：

输入：C1C2

输出：-1

说明：1)输入长度为n=2，第一个字节C0为11000001，第二个字节C0为11000010

那么二进制表示：11000001 11000010，那么第二位不是10开头，不合法。

解题思路：

1)判断：取出某几位方法使用按位与运算，把无关的位都置成0，然后用移位操作把几个需要的位移到最低位置。

2)输出：把几个位的数据复制到待输出数据的指定位置上，则可先统移位操作把几个位移到对应位置，然后通过按位或运算是的结果包含这几个位。这种也可以使用字符串截取、拼接完成得到结果。

 1     public static void getResult(String s) {
 2         int len = s.length();
 3         int n = len % 8 == 0 ? len >> 3 : (len >> 3) + 1;
 4         String resTmp = StringUtils.rightPad(s, n<<3, "F");
 5         if (n == 1) {
 6             System.out.println(resTmp);
 7         } else {
 8             String tmp = resTmp.substring(0, 8);
 9             for (int i=1; i< n; i++) {
10                 int idx = i << 3;
11                 tmp = Integer.toHexString(Integer.valueOf(tmp,16) ^ Integer.valueOf(resTmp.substring(idx, idx+8),16));
12             }
13             System.out.println(StringUtils.leftPad(tmp, 8, "0").toUpperCase());
14         }
15     }

思路二：

可以使用进制与或运算，消除无效位置数字

1)消除有效位，只保留首位几个判断位，分别进行判断，是否合规；

2)消除判断位，保留有效位，拼接得到最终结果。

 1     public static int getEncode(String encode) {
 2         int len = encode.length() >> 1;
 3         int byteNum = len;
 4         String tmpEncode = encode;
 5         StringBuilder sb = new StringBuilder(48);
 6         while (byteNum > 0) {
 7             Integer tmp = Integer.valueOf(tmpEncode.substring((byteNum - 1) << 1), 16);
 8             if (byteNum == 1) {
 9                 Integer subTmp = Integer.valueOf((tmp & ((1 << len) - 1) << (8 - len))) >> (7 - len);
10                 if (subTmp != (((1 << len) - 1) << 1)) {
11                     return -1;
12                 }
13                 sb.insert(0, Integer.toBinaryString(tmp & ((1 << (7 - len)) - 1)));
14             } else {
15                 Integer subTmp = Integer.valueOf((tmp & ((1 << 7) | (1 << 6))) >> 6);
16                 if (subTmp != 2) {
17                     return -1;
18                 }
19                 sb.insert(0, strRightPad(Integer.toBinaryString(tmp & ((1 << 6) - 1)), 6, '0'));
20             }
21             tmpEncode = tmpEncode.substring(0, (byteNum - 1) << 1);
22             byteNum--;
23         }
24         return Integer.valueOf(sb.toString(), 2);
25     }
26 
27     private static String strRightPad(String str, int size, char cha) {
28         if (str == null || str.length() >= size) {
29             return str;
30         }
31         StringBuilder sb = new StringBuilder();
32         char[] chars = str.toCharArray();
33         int idx = str.length();
34         for (int i = size; i > 0; i--) {
35             if (idx > 0) {
36                 sb.insert(0, chars[i - 1]);
37                 idx--;
38             } else {
39                 sb.insert(0, cha);
40             }
41         }
42         return sb.toString();
43     }

拓展延伸题：

算法题目三，是先判断字符是否满足特殊格式要求，满足后提取有效位进行拼接获取结果。然而，如果现在提供有效位，按照这种特殊格式进行拼接，获取拼接后的结果该如何做？

题目大概意思差不多：

1)单字节(n=1)，字节第一位1，其余为有效位

2)多字节(n>1且n<=6)，第一个字节前n位都为0，第n+1位为1；后面每个字节前2位都为01，其余是有效位。

二进制规则格式如下：

N=1：1xxxxxxx

N=2：001xxxxx 01xxxxxx

N=3：0001xxxx 01xxxxxx 01xxxxxx

…

N=6：0000001x 01xxxxxx 01xxxxxx 01xxxxxx 01xxxxxx 01xxxxxx

输入10进制数据，输出16进制结果(偶数位)，不足首位补0(即：右对齐，左侧补0)