C++ 不知算法系列之深入动态规划算法思想

1. 前言

前面写过一篇博文，介绍了什么是动态规划算法。动态规划算法的最大特点，原始问题可以通过分解成规模更小的子问题来解决，子问题之间互成依赖关系，先计算出来的子问题的结果会影响到后续子问题的结果。

有点类似于武侠片中，主角受伤后，一群江湖侠士排成一排，最后一人把真气传递给前面的、前面的再传递给他前面……如此传递，最后传递给主角，主角最终获取到所有人的真气。

真气传递过程中，每一个人就是一个子问题，如果每一个人传递出去的真气是个体最大的，则最后主角获取到的真气必然也是最大的。这便是动态规划的最优子结构的概念。

本文通过几个案例，深入探讨动态规划。

2. 案例

2.1 最短路径

2.1.1 问题描述

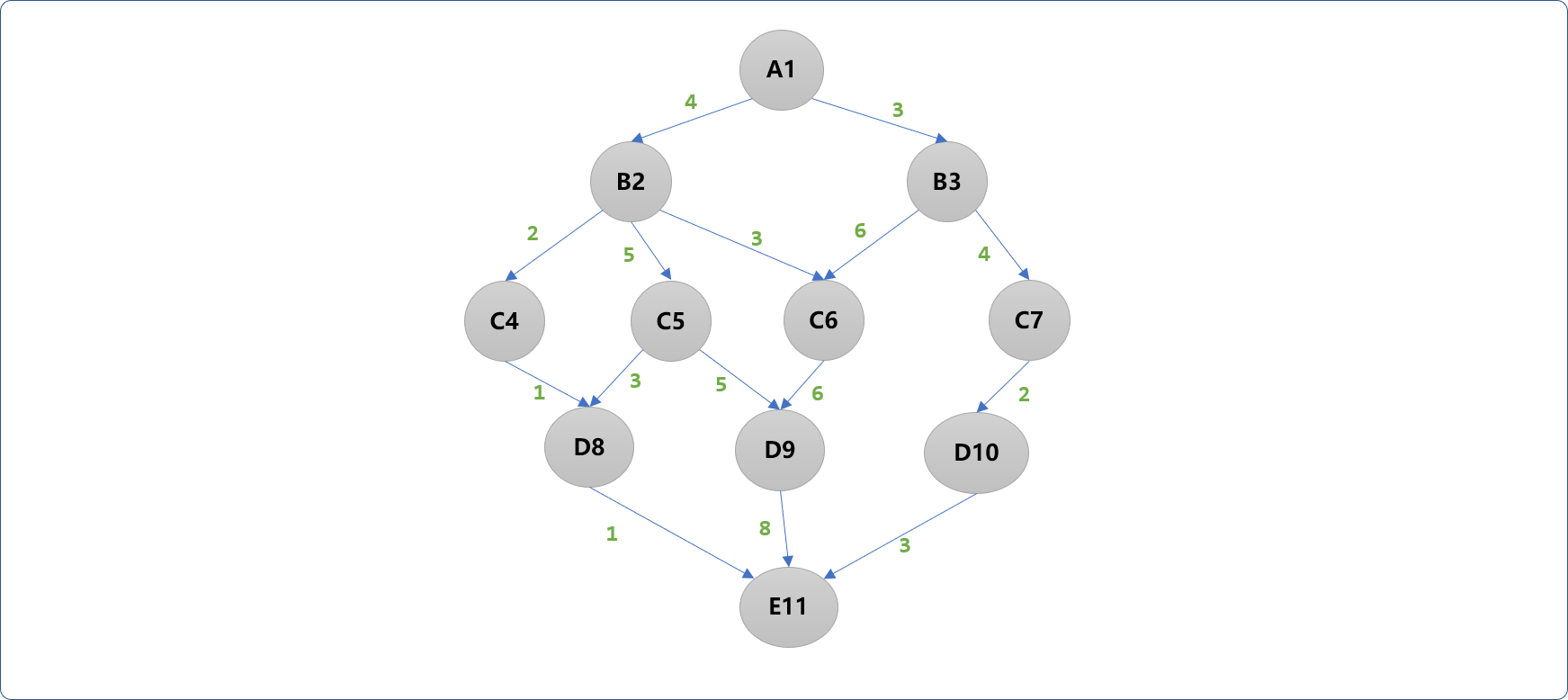
求解如下有向权重图中从A城市到E城市之间的最短路程。城市与城市之间的连接线上的数字表示城市之间的路程。

2.1.2 问题分析

动态规划是一种从下向上的解决方案，也就是逆推思维。

顺着这个思路，本题目可以先计算离E最近的D层到E的最短路程。D层上有 3 个顶点，意味着需要单独计算 3 次。如此可见，原始问题是可以拆分成多个子问题进行解决的，符合动态规划的条件之一：存在子问题。

为了分析问题的方便，给每一个结点一个编号（如上图，字母后面的数字便是结点的编号）。并且把任一结点到E结点的最短路程存储在一维数组中(也称为 db 数组)。

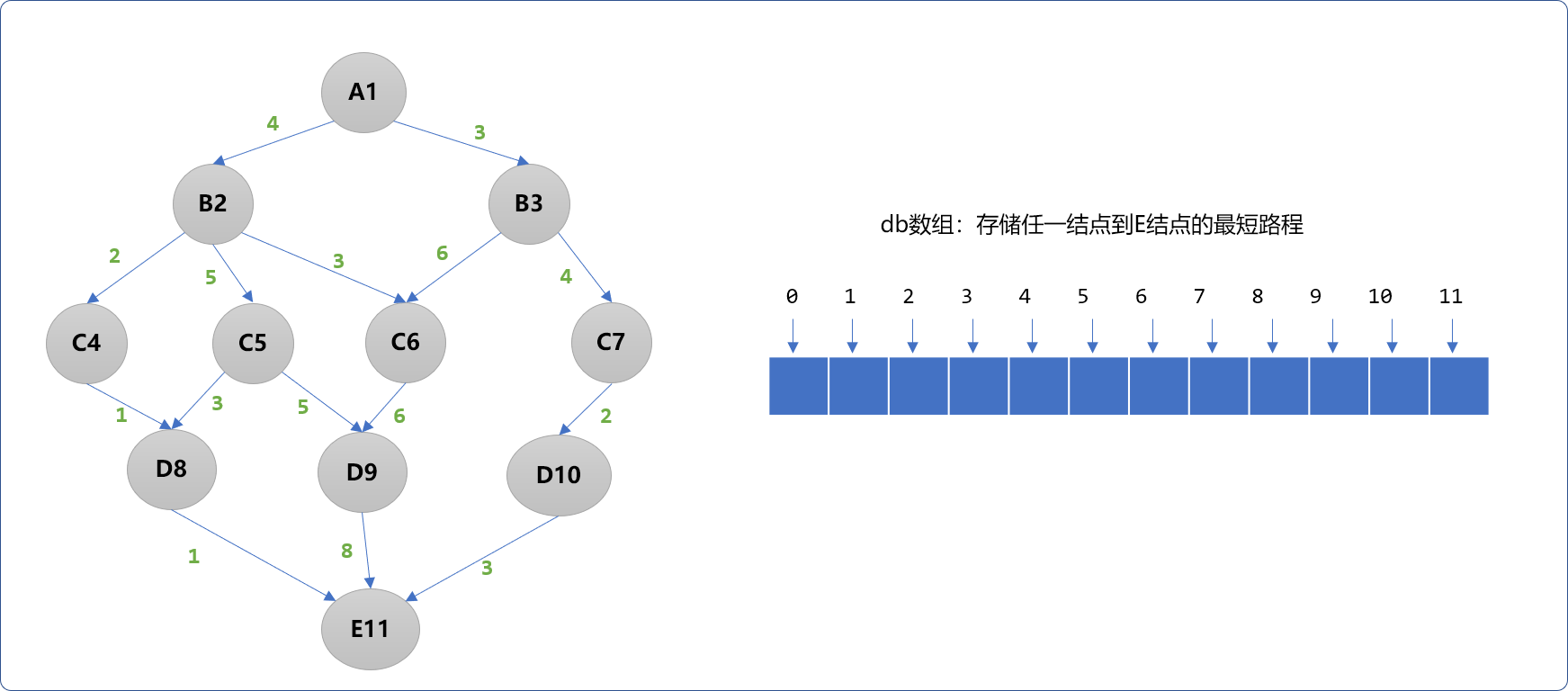
从D层到E是直达的，权重值即是最小值，可以直接存储。

C层到E层的路程计算原则。C4~E中间只经过D8，路程数为2，即C4～E 的最短路程为2。但是，C5~E中间可以经过D8和D9，C5~D8~E的路程数是4，C5~D9~E的路程数是13，则需要在两者中选择最小值，即min(4,13)，或说C5~E的最短路程是4。C6~E的最短路程为14,C7~E的最短路程为5。

Tips：

路径计算法则 ：当前结点到中间结点的权重加上中间结点到最终结点的最小路程值。

如 C5到E结点可以通过中间结点D8、D9到达，即有 2 条可行路径。

如计算 C5~D8~……E的路程值：C2到D8的权重加上D8到E 的最小路程值（可以从db数组中获取）。即：3+1。

路径选择原则：当存在多条路径时，选择值最小的。如上分别计算出 2 条路程值(4，13)后，再选择最小值，如此能得到C5~E的路径值 4 是最小的。

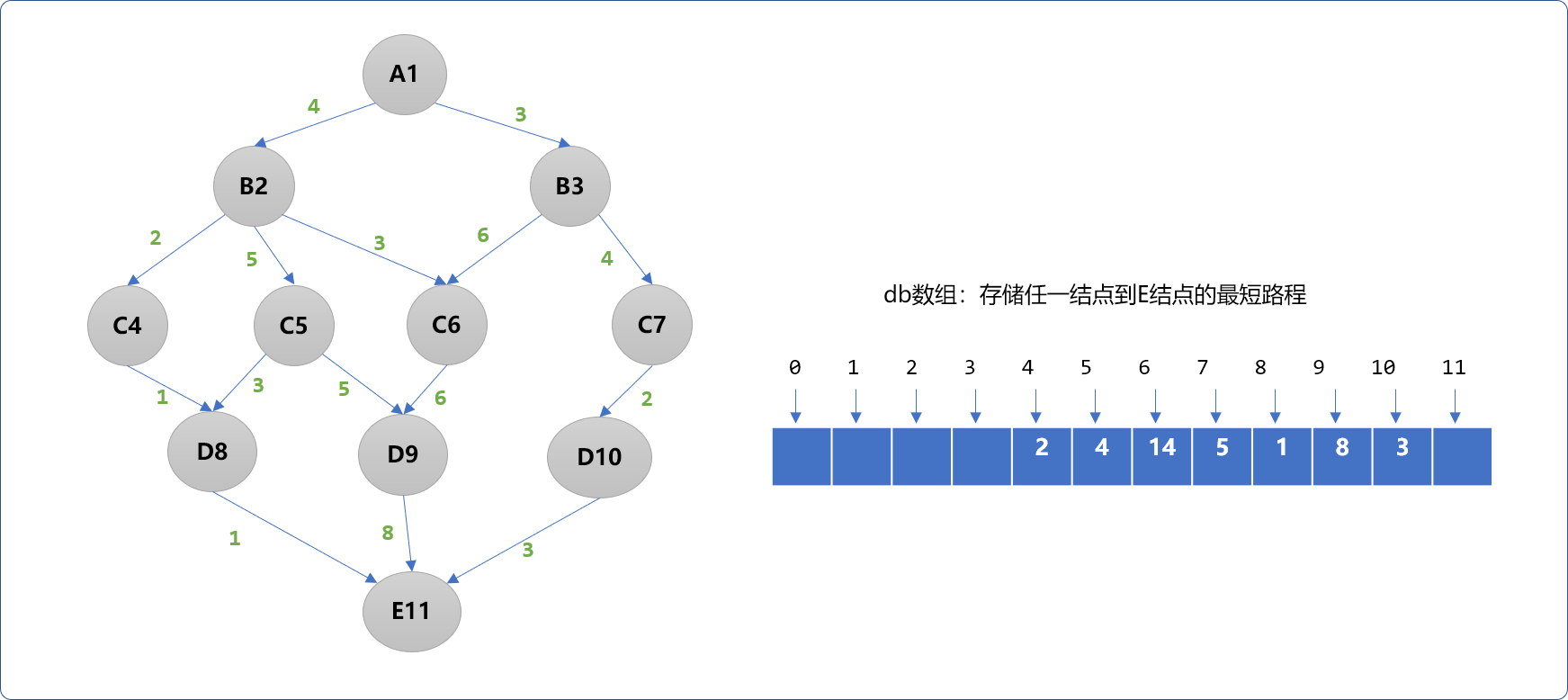
B层到E的最路短路程计算和上述是一样的。B2可以经过C4、C5、C6到达E，在 3 条路径中选择最小值 min(4,9,17)，即B2~E最短路程为4。B3可以经过C6、C7到达 E，同样在 2 条路径中选择最小值 min(20,9)。即B2~E 最短路径为9。

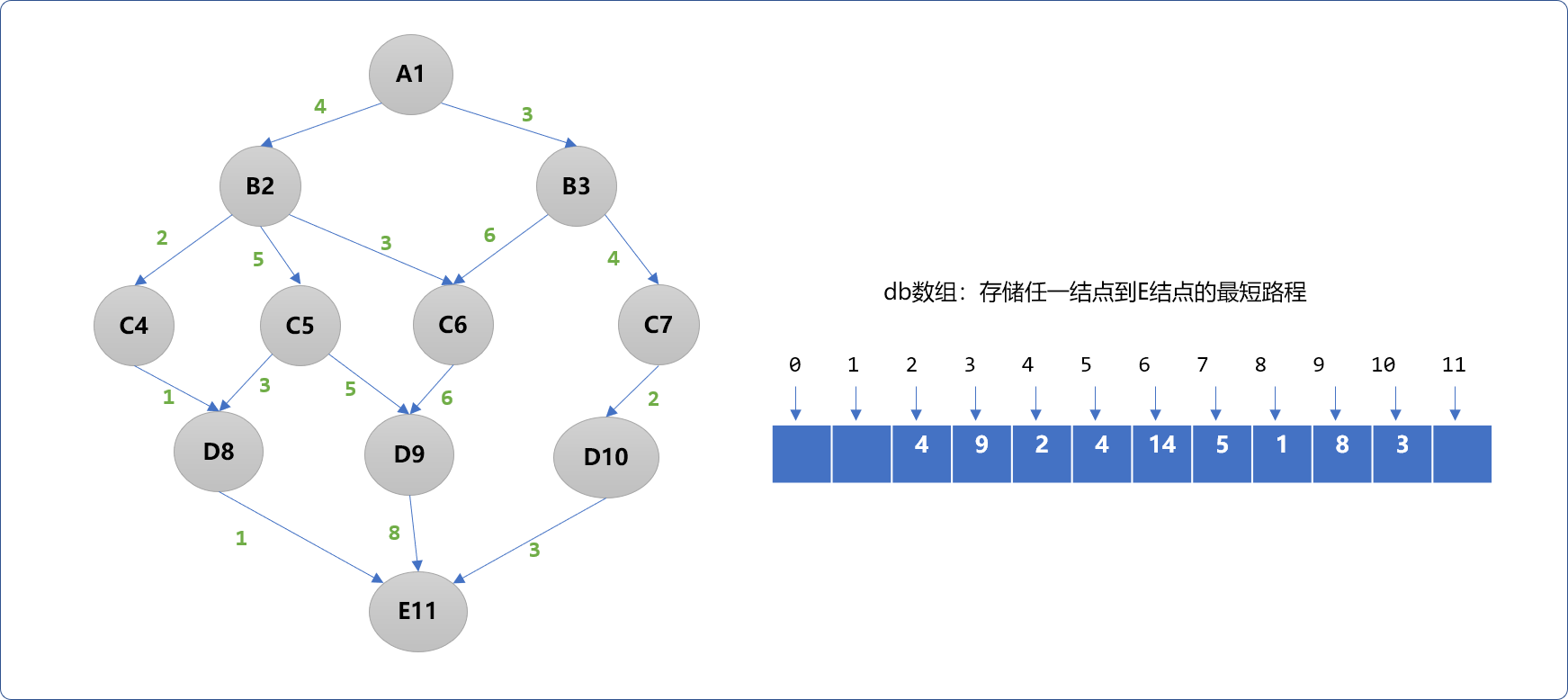
A1可以经过B2、B3到达E，在 2 条路径中选择最小值，即min(8,12)。最终可知A~E的最短路程为8。

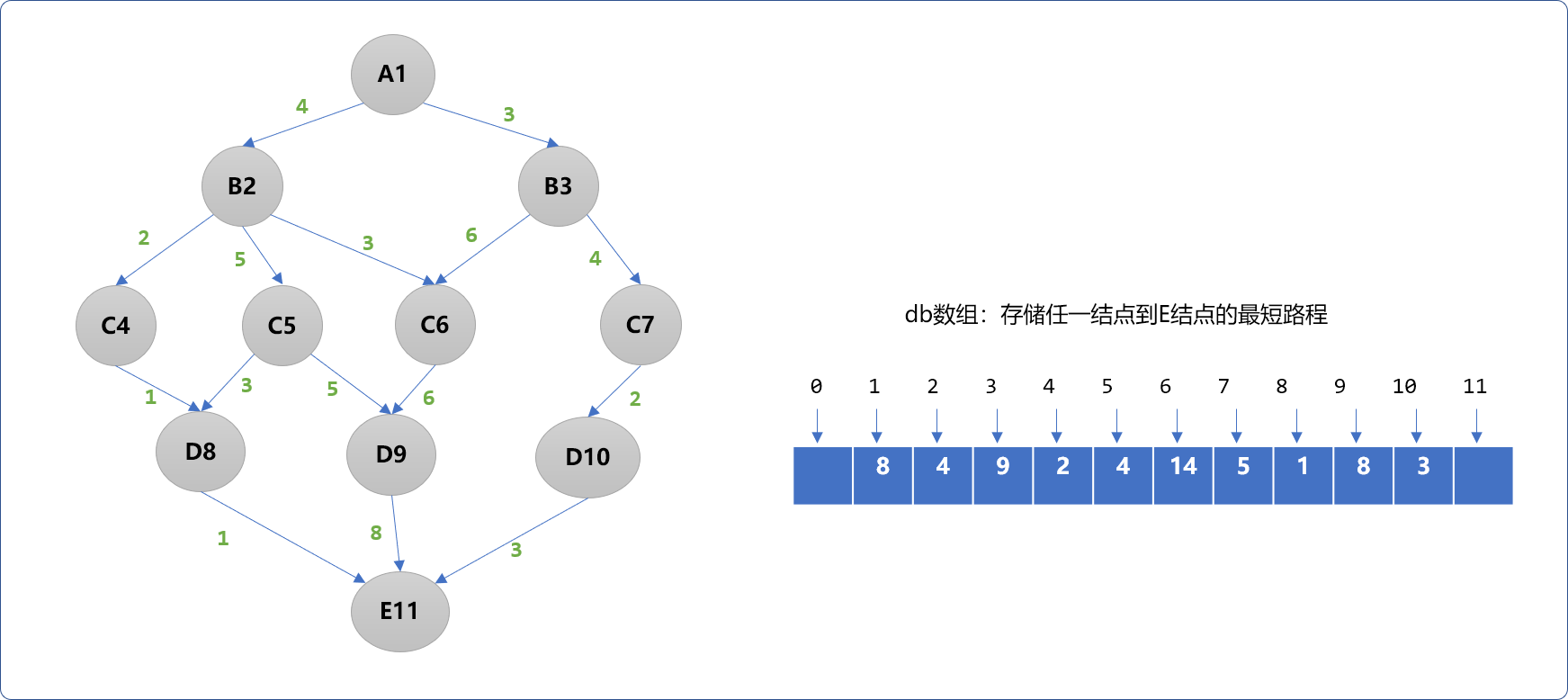
如上述流程可知，向上逆推过程中，求解到每一层到达E结点的最短路程后，再把最小值向上层提供，显然，最后所求解的值一定是最小值，也称为最优子结构思想。不仅能求解出A~E的最短路径，并且能求解出每一个结点到达E的最短路程。

2.2.3 编程实现

动态规划算法中，有 2 个非常重要的信息需要获取：

存储子问题的状态信息(本题指子问题到最终结点的最短路程)。如上述演示图中的db一维数组。
另就是状态求解方程式。通过上述分析可知，f(v)=min( w(v,v1)+db(v1), w(v,v2)+db(v2),…… )。

问题域本身也有 2 个信息：

结点数据。
结点之间的关系数据。

#include <iostream>
#include <map>
#define INT_MAX 0x7fffffff
using namespace std;
int getMin(int num1,int num2) {
	return num1<num2?num1:num2;
}
//测试
int main(int argc, char** argv) {
	//状态信息表
	int db[12]= {0};
	//对结点进行编号，并存储存结点信息
	string verNames[12]= {"","A1","B2","B3","C4","C5","C6","C7","D8","D9","D10","E11"};
	//邻接矩阵表，存储结点之间的关系
	int matrix[12][12]= {  { 0,0,0,0,0,0,0,0,0,0,0,0 },
		{	0,0,4,3,0,0,0,0,0,0,0,0 },
		{	0,0,0,0,2,5,3,0,0,0,0,0 },
		{	0,0,0,0,0,0,0,4,0,0,0,0 },
		{	0,0,0,0,0,0,0,0,1,0,0,0 },
		{	0,0,0,0,0,0,0,0,3,5,0,0 },
		{	0,0,0,0,0,0,0,0,0,6,0,0 },
		{	0,0,0,0,0,0,0,0,0,0,2,0 },
		{	0,0,0,0,0,0,0,0,0,0,0,1 },
		{	0,0,0,0,0,0,0,0,0,0,0,8 },
		{	0,0,0,0,0,0,0,0,0,0,0,3 },
		{	0,0,0,0,0,0,0,0,0,0,0,0 }
	};
	//从编号为 10 的结点开始向上计算
	for(int i=10; i>0; i--) {
		//最小值
		int minVal=INT_MAX;
		for(int j=1; j<12; j++) {
            //得到相邻结点的权重和相邻结点到最终点的最短路程，
			if( matrix[i][j]!=0 &&  matrix[i][j]+db[j] < minVal ) {
                 //找到最小值，本题目的关键所在
				minVal= matrix[i][j]+db[j];
			}
		}
		db[i]=minVal;
	}
    //输出所有最小短路
	for(int i=1; i<11; i++) {
		cout<<verNames[i]<<"~E 的最短路程："<< db[i]<<endl;
	}
	return 0;
}

输出结果：

2.2 找零钱

2.2.1 问题描述

给你k种面值的硬币，面值分别为c1, c2 ... ck，每种硬币的数量无限，再给一个总金额amount，问最少需要几枚硬币凑出这个金额，如果不可能凑出，算法返回 -1 。

比如说k = 3，面值分别为 1，2，5，总金额amount = 11。那么最少需要 3 枚硬币凑出，即 11 = 5 + 5 + 1。

2.2.2 分析问题

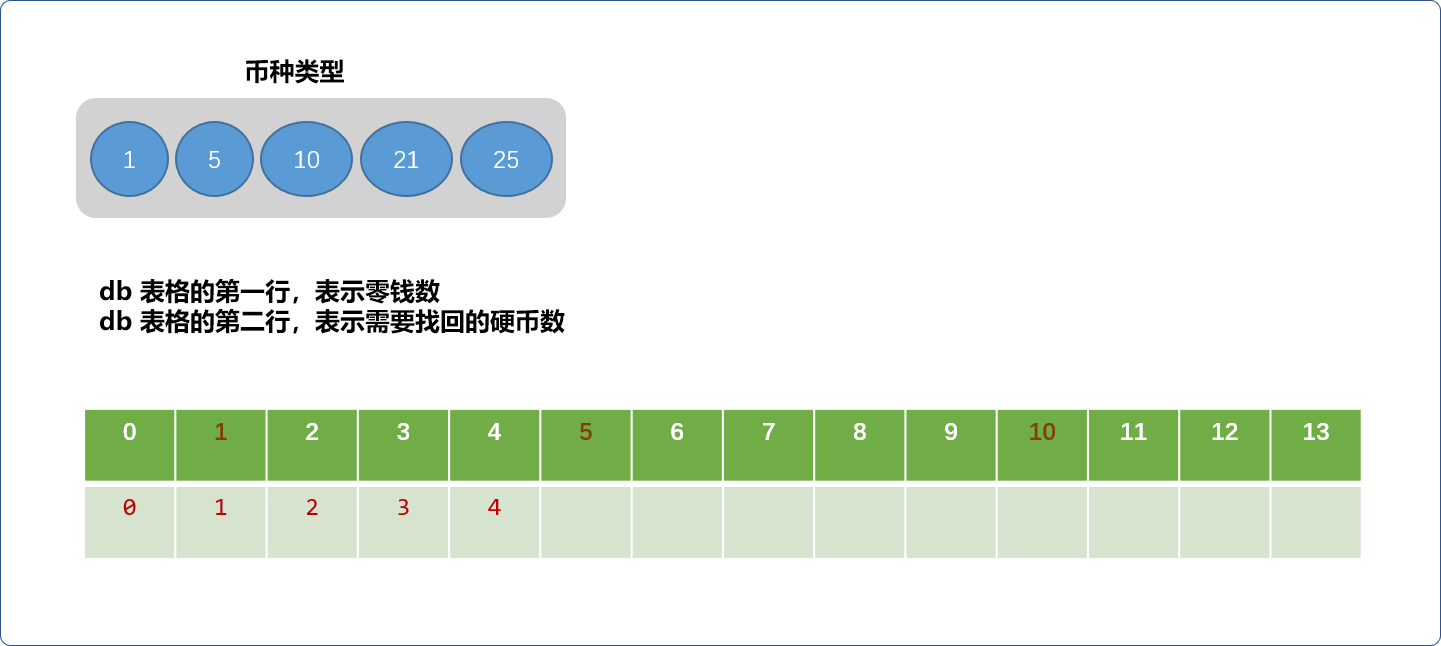
假设现有面值为 {1,5,10,21,25}的币种，需要找的零钱是 63（单位都是分）。

当零钱为 1,2，3,4分时，都只能由 1 分的硬币组成，找回的硬币数分别是：1枚，2枚，3枚，4枚。如下图所示：

当找零为 5 时，可以有 2 种选择方案。先找出 1 枚 1 分硬币，然后计算 5-1=4分钱需要找回多少硬币，因为 4分要找回 4个硬币，共需要 5 枚。另就是直接拿出一枚 5 分硬币，显然，1 枚更少。

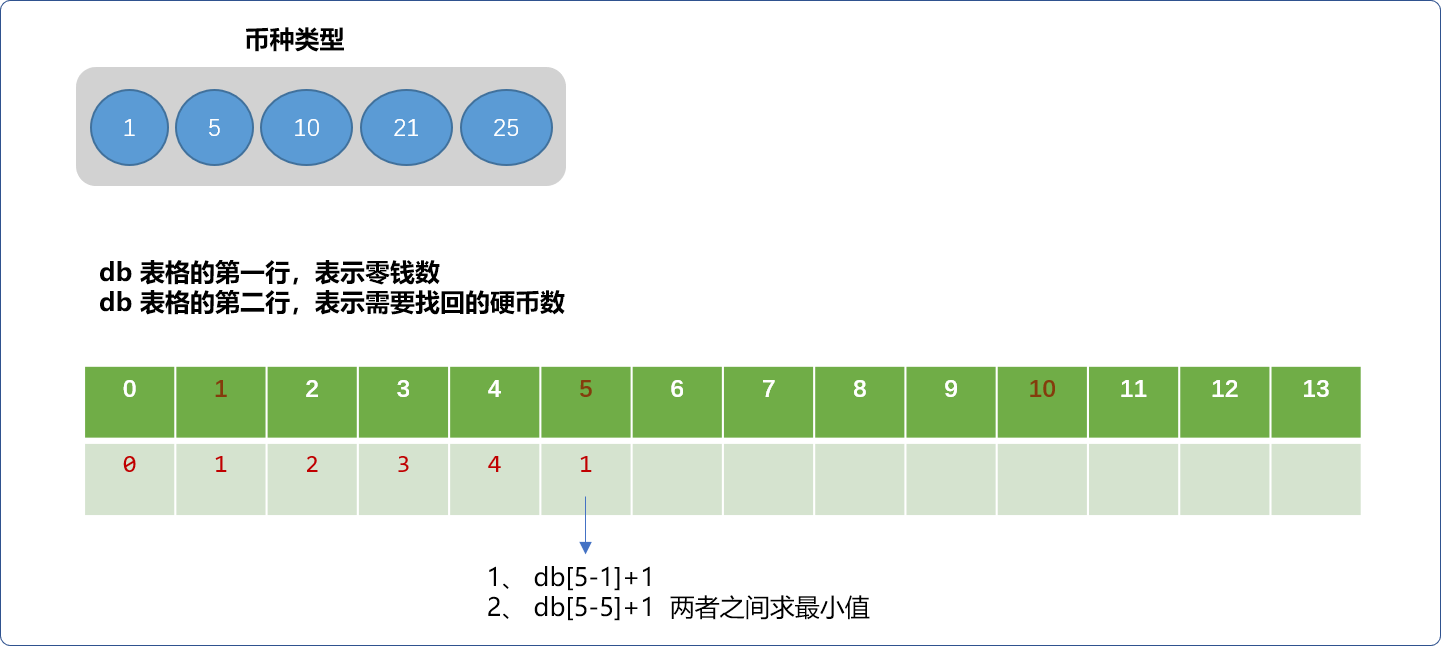
当找零为 6 时，也有 2 种方案，先拿出一枚 1 分硬币，再计算剩下的 5 分钱最少需要找回多少硬币。另一个方案就是拿出一枚 5分硬币，计算剩下的 1 分钱需要找回的最少硬币。

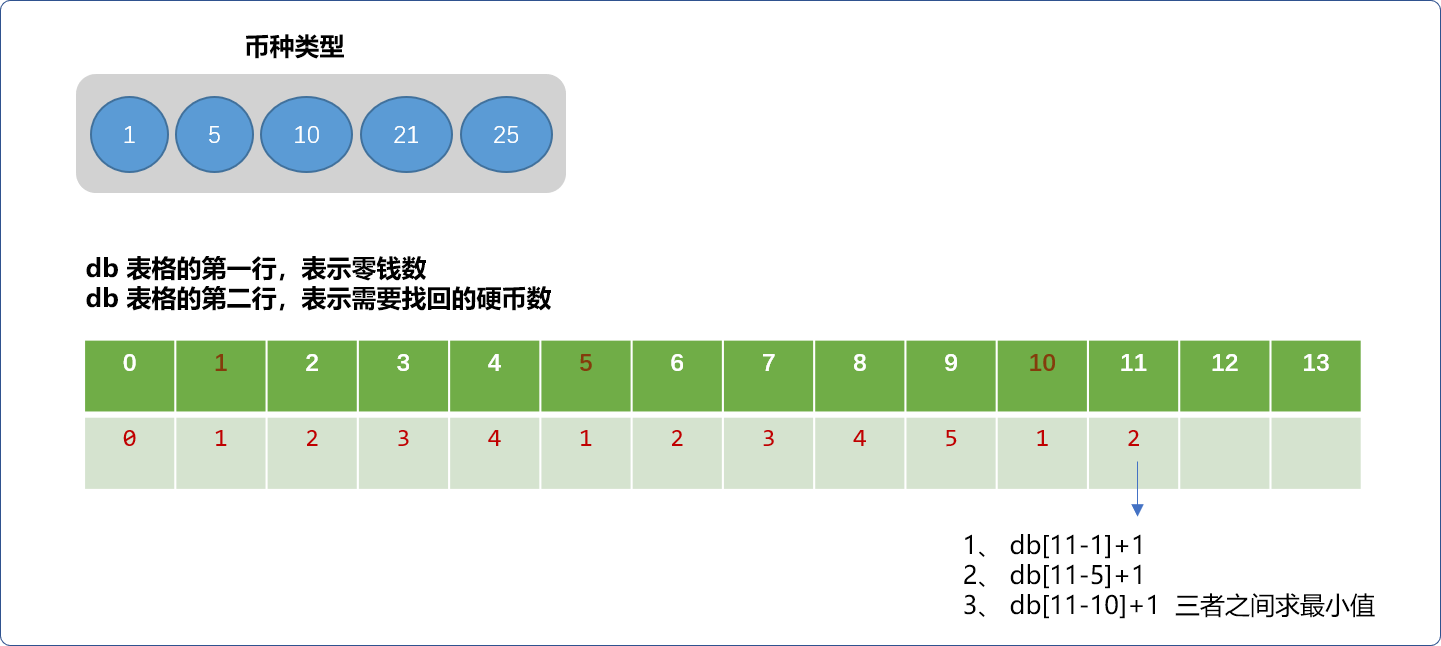
当找零为 11 时，则会有 3 种方案，可以得到一个结论，方案的多少由小于此零钱的币种数决定。原理很简单，对于 11 分钱的零钱而言，可以先拿出一枚 1分的硬币，也可以先拿出一枚5分的硬币，或者是拿出一枚 10分的硬币，然后再计算剩下的钱需要找回多少硬币。

2.2.3 编码实现

#include <iostream>
#include <vector>
using namespace std;
int main(int argc, char** argv) {
	int money=0;
	cout<<"请输入零钱数:"<<endl;
	cin>>money;
	//硬币类型
    int coins[5]= {1,5,10,21,25};
	//状态数组，零钱需要找回的硬币数
	vector<int> dp(money+1, money+1);
	dp[0]=0;
	for(int i=1; i<=money; i++) {
		for(int j=0; i>=coins[j]; j++) {
             //求最小值            
			dp[i]=dp[i] < dp[ i-coins[j] ]+1 ? dp[i] : dp[ i-coins[j] ]+1;	    	
		}
	}
	cout<<dp[money]<<"\t";
	return 0;
}

输出结果：

2.3 背包问题

2.3.1 问题描述

有一个可装载重量为W的背包和N个物品，每个物品有重量和价值两个属性。其中第i个物品的重量为wt[i]，价值为val[i]，现在用这个背包装物品，最多能装的价值是多少？

Tips： 题目中的物品不可以分割，要么装进包里，要么不装，不能切成两块装一半。

如输入如下数据：

N = 3, W = 6
wt = [ 1,2,7 ]
val = [4,3,2 ]

可以选择前两件物品装进背包，总重量 3 小于W，可以获得最大的价值是 7。

本题依然使用动态规划算法解决。

2.3.2 问题分析

从本文上面 2 道题目的解决过程可知，解决问题不是一趋而蹴，总是从一个很小的问题开始进行推导。本题一样，可以先简化问题，一旦找到问题的规律后，便可放大问题。

背包问题，有 2 个状态值，背包的容量和可选择的物品。

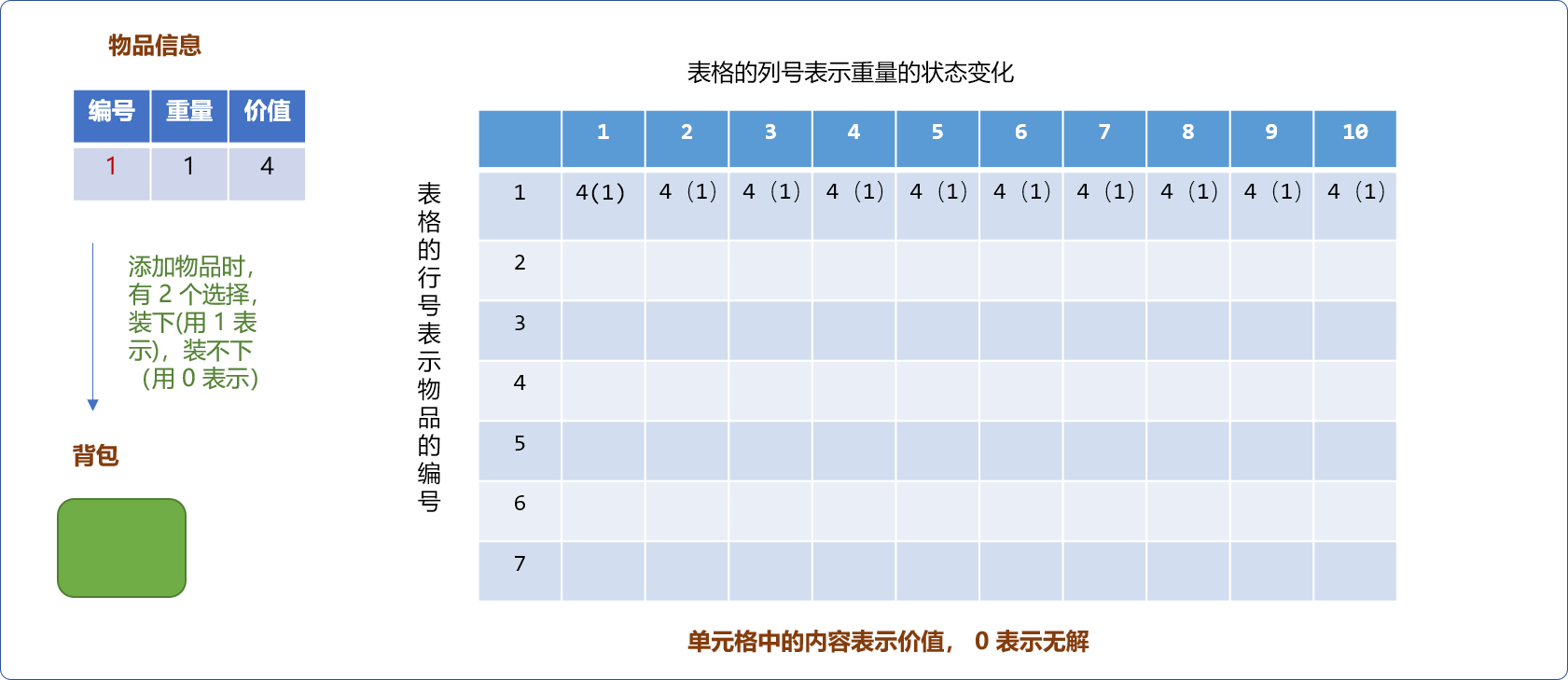
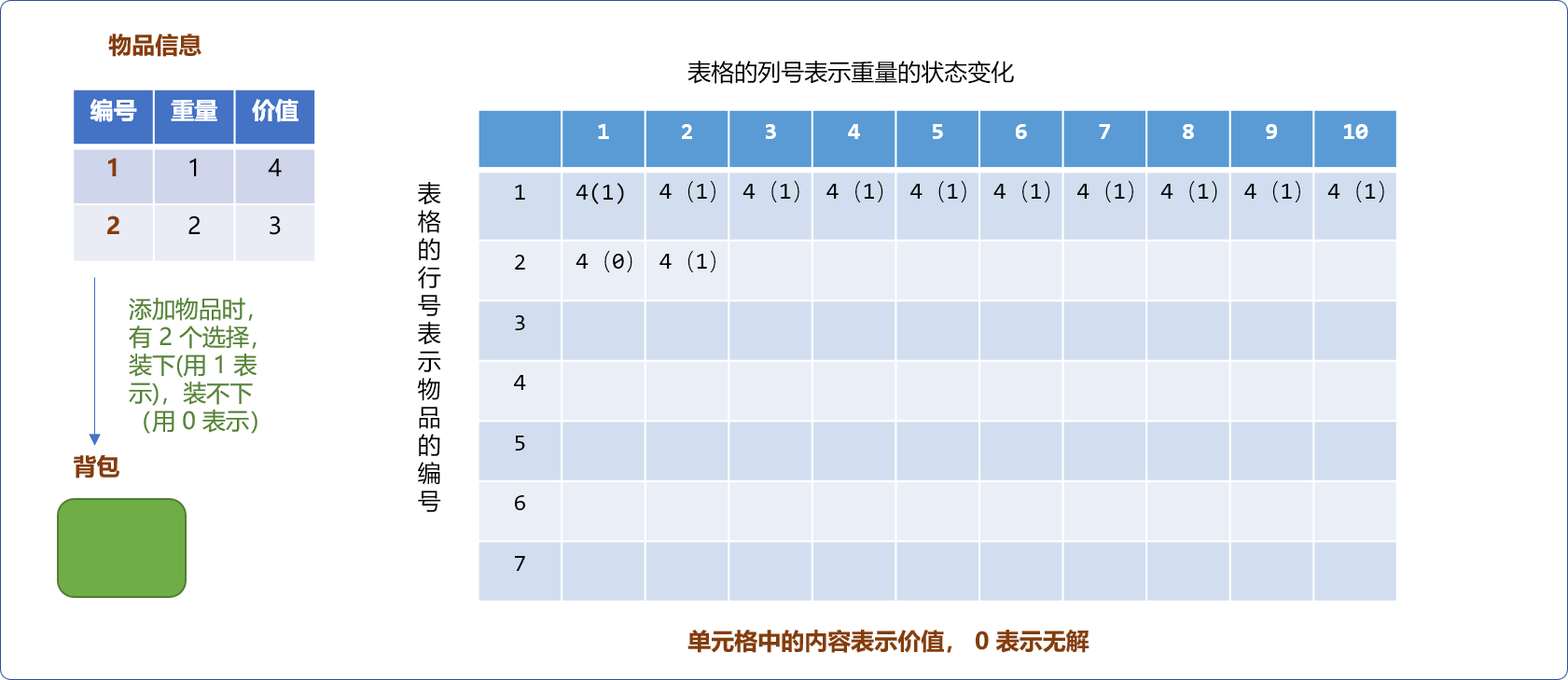
物品对于背包而言，只有 2 种选择，要么装下物品，要么装不下，如下图所示，表格的行号表示物品编号，列号表示背包的重量。单元格中的数字表示背包中最大价值。当物品只有一件时，当物品重量大于背包容量，不能装下，反之，能装下。如下图，物品重量为 1。无论何种规格容量的背包都能装下（假设背包的容量至少为 1）。

如下图，当增加重量为 2 的物品后，当背包的容量为 1 时，不能装下物品，则最大值为同容量背包中已经有的最大值。

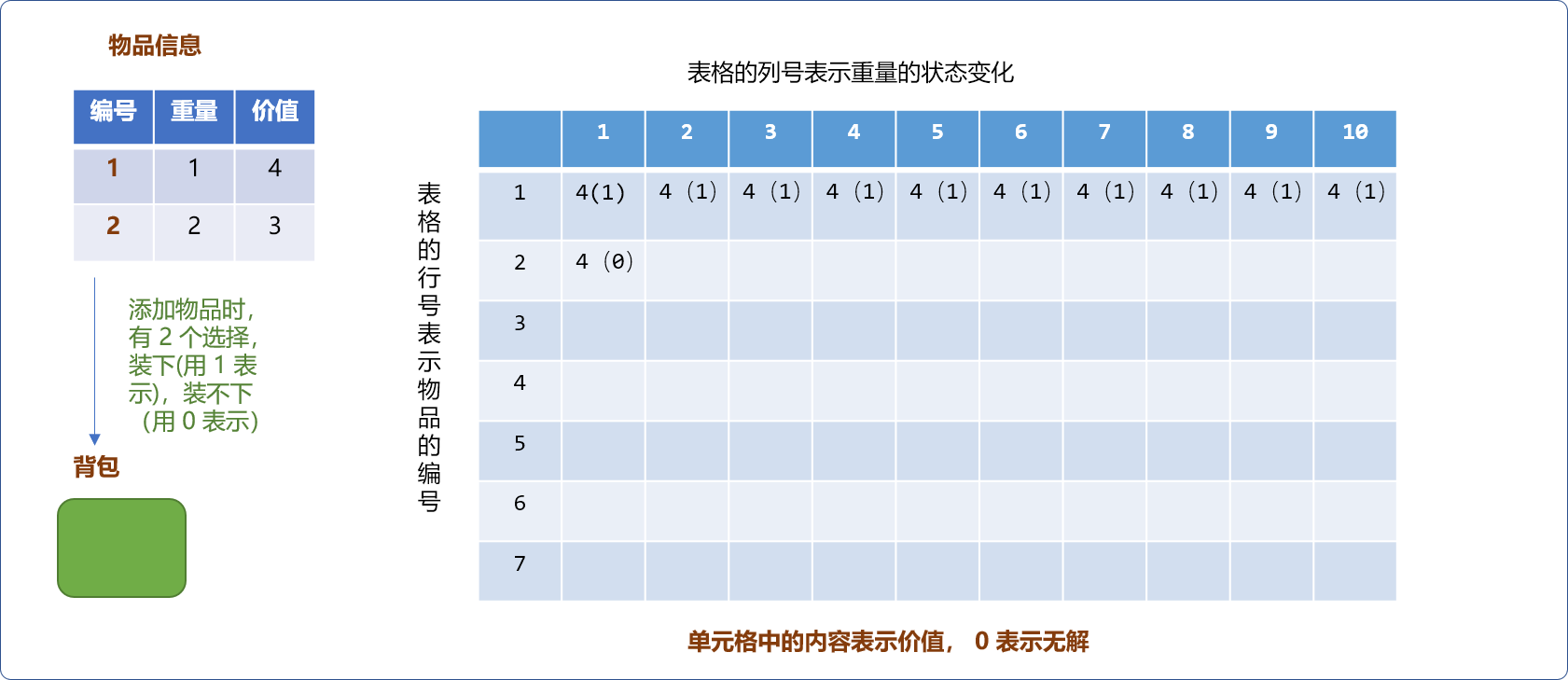
但对容量为 2的背包而言，恰好可以放入新物品，此时背包中的最大价值就会有 2 个选择，一是把物品 2 放进去，背包中的价值为 3。二是保留背包已有的价值4。然后，在两者中选择最大值 4。

当背包容量是 3时，物品2也是可以放进去的。此时背包的价值可以是当前物品的价值 3加上背包剩余容量3-2=1能存放的最大价值4，计算后值为 7。要把此值和不把物品放进去时原来的价值 4 之间进行最大值选择。

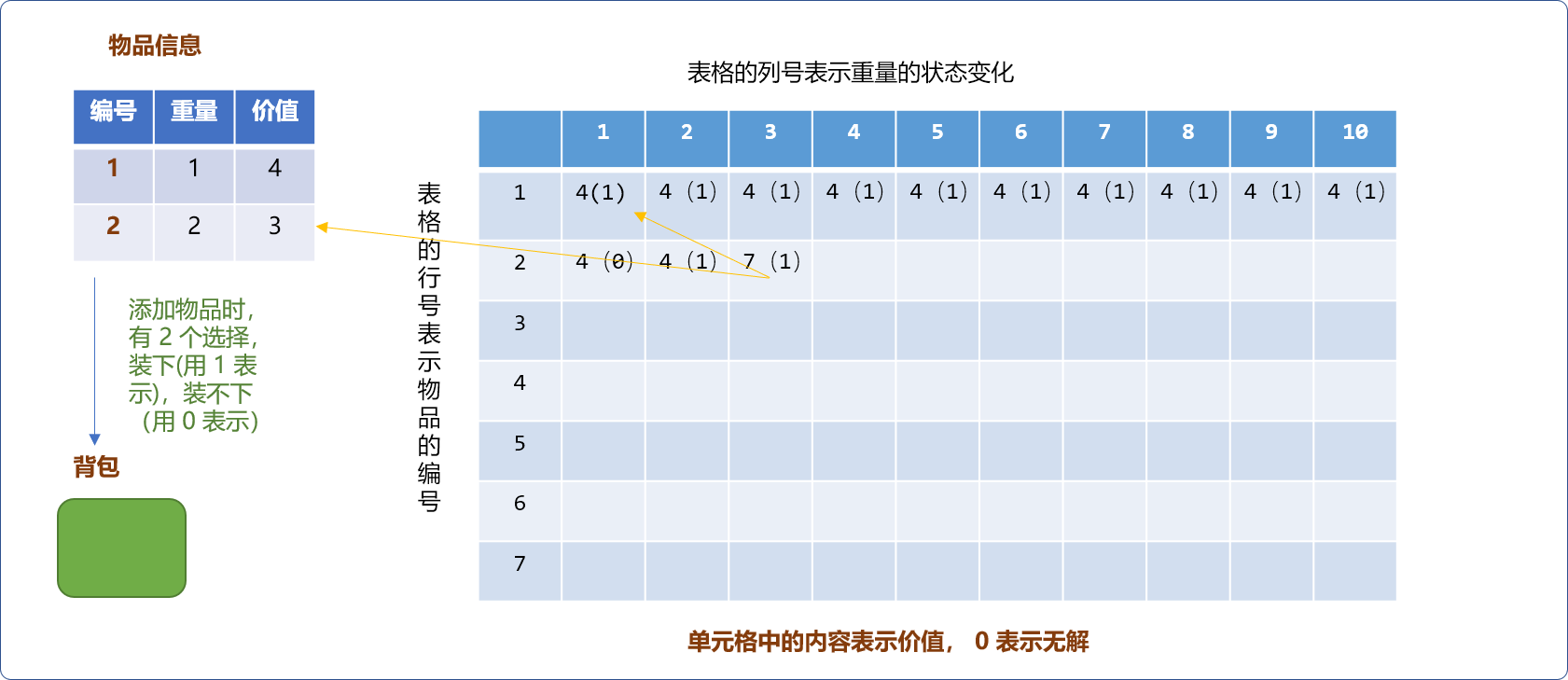
所以，对于背包问题，核心思想就是：

如果物品能放进背包：则先计算出物品的价值加上剩余容量能存储的最大价值之和，再找到不把物品放进背包时背包中原有价值。最后在两者之间进行最大值选择。
当物品不能放进背包：显然，保留背包中原来的最大价值信息。

2.3.3 编码实现

#include <iostream>
#include <vector>
using namespace std;
int main(int argc, char** argv) {
	//物品信息
	int goods[3][3]= { {1,4},{2,3} };
	//背包容量
	int bagWeight=0;
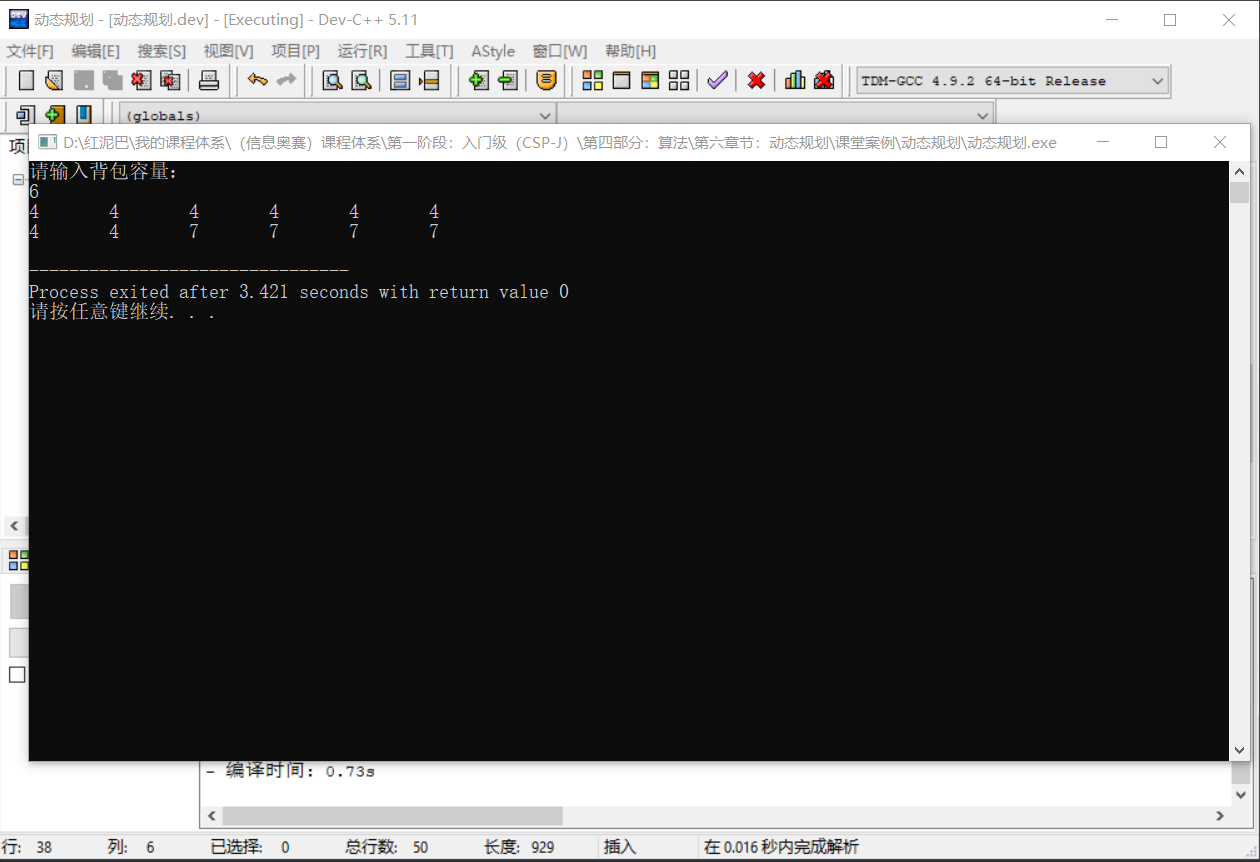
	cout<<"请输入背包容量："<<endl;
	cin>>bagWeight;
	//状态表
	int db[4][bagWeight+1]= {0};
	for(int i=0; i<4; i++) {
		for(int j=0; j<bagWeight+1; j++) {
			db[i][j]=0;
		}
	}
	for(int w=1; w<4; w++) {
		for(int wt=1; wt<=bagWeight; wt++) {
			if( goods[w-1][0]>wt ) {
				//如果背包不能装下物品，保留背包上一次的结果
				db[w][wt]=db[w-1][wt];
			} else {
				//能装下,计算本物品价值和剩余容量的最大价值
				int val=goods[w-1][1] + db[w-1][ wt- goods[w-1][0] ];
				//背包原来的价值
				int val_= db[w-1][wt];
				//计算最大值
				db[w][wt]=val>val_?val:val_;
			}
		}
	}
	for(int i=1; i<3; i++) {
		for(int j=1; j<=bagWeight; j++) {
			cout<<db[i][j]<<"\t";
		}
		cout<<endl;
	}
	return 0;
}

输出结果：