聚类概念

聚类是一种无监督的机器学习方法，它主要是通过在数据集中找到相似的样本并将它们分组来发现数据中的模式和结构。聚类算法可以将数据分成具有相似特征的组，每个组被称为一个簇。

常见的聚类算法有以下几种：

K-means聚类算法：它是最常见的聚类算法之一，它的目标是将数据集分为K个簇，使得每个簇内的数据点相似度最高，不同簇之间的差异最大。
层次聚类算法：该算法将数据集中的样本逐渐合并到一起，直到形成一个完整的聚类结构，从而形成一颗聚类树。
密度聚类算法：它是一种基于数据点密度的聚类算法，它将数据点分为密集的区域和稀疏的区域，并将密集区域看作是一个簇。
均值漂移聚类算法：该算法使用核密度估计来找到数据点的局部最大值，以确定簇的质心。
DBSCAN聚类算法：它基于在数据集中的密度来确定簇的个数和形状，它可以识别任意形状的簇。

K-means简介

K-means是一种基于距离度量的聚类算法，其主要思想是将数据集分成K个簇，每个簇包含距离最近的K个数据点。该算法通过迭代优化簇的中心点，来不断调整簇的划分，最终得到一组最优的簇划分结果。

通俗来说，K-means算法就像是一位假设聪明的小学生在玩“猜数字”游戏。他会先猜一个数字，然后根据猜测与正确答案的距离（越接近答案距离越小），将答案所在的数字范围分成两个区域。接着，他会重复这个过程，直到将数字范围分成了K个区域为止，并记录下每个区域的中心点。最后，他会告诉你每个数字应该属于哪个区域（或者说簇），并告诉你每个区域的中心点。

在K-means算法中，我们需要指定簇的个数K，然后随机选择K个数据点作为初始中心点。接着，我们计算每个数据点距离各个中心点的距离，并将其归入距离最近的簇中。然后，重新计算每个簇的中心点，并重复上述过程（在计算每个点到新中心的举例重新归类到簇），直到簇的中心点不再发生变化为止。最终，我们将得到K个簇，每个簇包含一组距离最近的数据点，并且每个数据点只属于一个簇。

需要注意的是，由于K-means算法的初始中心点是随机选择的，因此可能会得到不同的簇划分结果。为了获得更好的结果，可以多次运行算法，并选择最优的簇划分结果。

K-means和KNN区别

K-Means和K-NN是两种不同的机器学习算法，其区别如下：

K-Means是一种聚类算法，它将数据集划分为K个簇，并将每个数据点分配到其最近的簇中心。K-NN是一种分类算法，它根据最近邻居的标签来预测新数据点的标签。
K-Means需要指定簇的数量K，而K-NN不需要。
K-Means是一种无监督学习算法，它不需要标记数据，而K-NN是一种监督学习算法，需要标记数据。
K-Means使用欧几里得距离来计算数据点之间的相似度，而K-NN可以使用不同的距离度量，如曼哈顿距离、余弦相似度等。
K-Means在处理大规模数据时可能会遇到性能问题，而K-NN可以轻松处理大规模数据。

总的来说，K-Means和K-NN是两种不同的机器学习算法，适用于不同的问题和数据集。

Kmeans的计算过程

（1）适当选择c个类的初始中心；
（2）在k次迭代中，对任意一个样本，求其到c各中心的距离（欧式距离），将该样本归到距离更短的中心所在的类；
（3）利用均值等方法更新该类的中心值；
（4）对于所有的c个聚类中心，如果利用（2）（3）的迭代法更新后，值保持不变，则迭代结束，否则继续迭代。

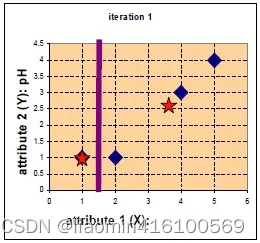
假设现在有4组数据，每组数据有2个维度，对其进行聚类分为2类，将其可视化一下。
$A = (1, 1), B = (2, 1), C = (4, 3), D = (5, 4)$
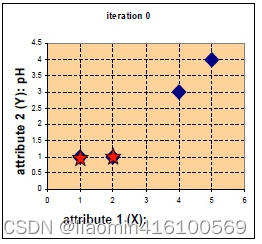
在这里插入图片描述
假设选取两个星的位置为初始中心 $c_1=(1,1),c_2=(2,1)$ ，计算每个点到初始中心的距离，使用欧式距离得到4个点分别距离两个初始中心的距离，归于最近的类：

$D^0第一行表示ABCD四个点到c1的举例，第二行表示ABCD四个点到c2的举例，举例使用欧氏距离公式计算出来，以C为例，到c1这一组的举例是3.61,到c2这一组的举例是2.83说明第一次迭代C是属于group-2$

通过比较，将其进行归类。并使用平均法更新中心位置。
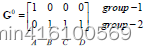
在这里插入图片描述
由于归于group1的只有一个点，一次更新后的中心位置 $c_1=(1,1)$ ，而 $c_{2} = (\frac{11}{3}, \frac{8}{3})$

group2的新中心点也就是 $x={(x1+x2+x3)\over 3} ={(2+4+5)\over3}={11\over3}$
$y={(y1+y2+y3)\over 3} ={(1+3+4)\over3}={8\over3}$

再次计算每个点与更新后的位置中心的距离

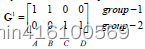
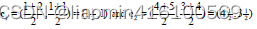
在这里插入图片描述

继续迭代下去，

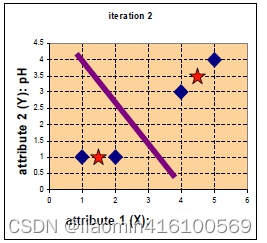
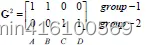
此时，与上一次的类别标记无变化，即可停止。

Kmeans的编程实现

#%%

from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

# 生成随机数据
X, y = make_blobs(n_samples=300, centers=4, random_state=42)

# 使用KMeans算法进行聚类
kmeans = KMeans(n_clusters=4, random_state=42)
kmeans.fit(X)

# 绘制聚类结果
plt.scatter(X[:, 0], X[:, 1], c=kmeans.labels_, cmap='viridis')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], marker='*', s=150, color='red')
plt.show()

在这里插入图片描述