堆是什么？

1. 堆是一种特殊的完全二叉树。
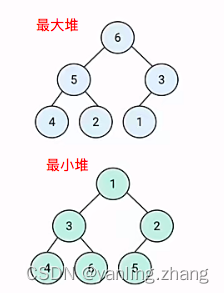
   完全二叉树：每层节点都完全填满，最后一层若是没填满，则只缺少右边的节点。
2. 所有的节点都大于等于（最大堆）或小于等于（最小堆）它的子节点。
3. javascript中通常使用数据表示堆。
4. 左侧节点的位置是： 2 * index + 1, 右侧节点的位置： 2 * index + 2
5. 父节点的位置：(index - 1) / 2

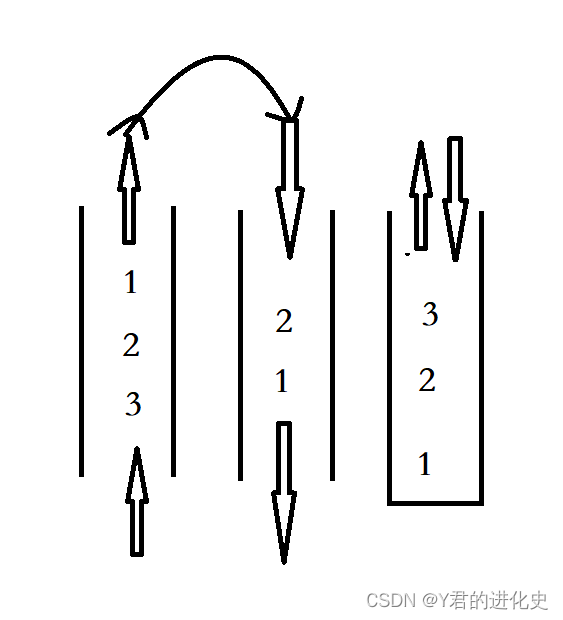
堆如下图：

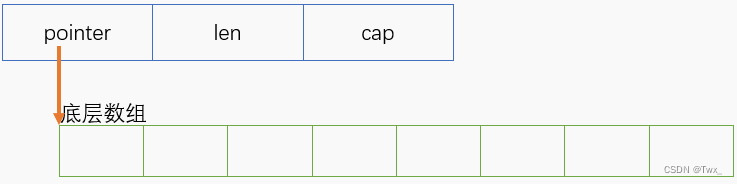
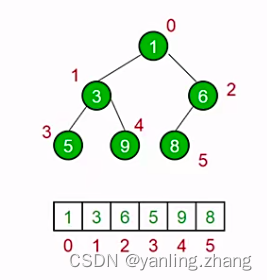
js中的堆：

堆的应用：

1. 高效快速的找出最大值，最小值。（时间复杂度 O(1)）
2. 找出第k个最大元素。
   

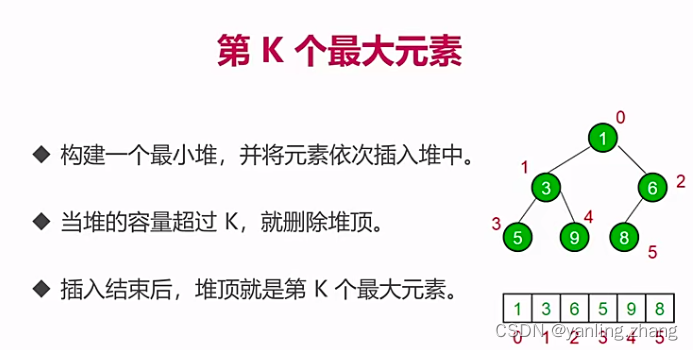
实现最小堆类

1. 在类里，声明一个数组，用来装元素。
2. 主要方法：插入，删除堆顶，获取堆顶，获取堆的大小。

插入：将值插入堆的底部，即数组的尾部。然后上移，将这个值和它的节点进行交换，直到父节点小于等于这个插入的值。

大小为k的堆中插入元素的时间复杂度为O(logk)

class MinHeap {
      constructor() {
        // 构建的堆
        this.heap = []
      }
      // 获取父节点
      getParentIndex(i) {
        return i - 1 >> 1
      }
		// 获取左子节点
		getLeftIndex() {
			return i * 2 + 1
		}
		// 获取右子节点
		getRightIndex() {
			return i * 2 + 2
		}
      // 交换2个节点的值
      swap(i1, i2) {
        const temp = this.heap[i1]
        this.heap[i1] = this.heap[i2]
        this.heap[i2] = temp
      }
      // 插入
      insert(value) {
        this.heap.push(value)
        this.shiftUp(this.heap.length - 1)
      }
      // 上移
      shiftUp(index) {
        if (index == 0) return
        const parentIndex = this.getParentIndex(index)
        // 如果父节点的值 大于 当前节点的值
        if (this.heap[parentIndex] > this.heap[index]) {
          // 交换两个节点的值
          this.swap(parentIndex, index)
        }
      }
		
		// 删除数组的最后一个元素，并且返回
		pop() {
			this.heap[0] = this.heap.pop()
			this.shiftDown(0)
		}
		
		// 下移
		shiftDown(index) {
			const leftIndex = this.	getLeftIndex(index)
			const rightIndex = this.getRightIndex(index)
			// 左侧节点的值 < 当前节点的值
			if (this.heap[leftIndex] < this.heap[index]) {
				this.swap(leftIndex, index)
				this.shiftDown(leftIndex)
			}
			if (this.heap[rightIndex] < this.heap[index]) {
				this.swap(rightIndex, index)
				this.shiftDown(rightIndex)
			}
		}
		// 获取堆顶
		peek() {
			return this.heap[0]
		}
		// 获取堆的大小
		size() {
			return this.heap.length
		}
    }


    const h = new MinHeap()
    h.insert(3)
    h.insert(2)
    h.insert(1)
    console.log(h.heap) // [1,3, 2]

删除堆顶：

1. 用数组尾部元素替换堆顶，（直接删除堆顶回破坏堆结构）
2. 然后下移：将新堆顶和它的子节点进行交换，直到子节点大于等于这个新堆顶。
3. 大小为k的堆中插入元素的时间复杂度为O(logk)

获取堆顶和堆的大小：
获取堆顶：直接返回数组的头部。
获取堆的大小：返回数组的长度。

leetCode 215.数组中的第k个最大元素

在未排序的数组中找到第k个最大的元素。请注意，你需要找的是数组排序后的第k个最大的元素，而不是第k个不同的元素。

var findKthLargest = function (nums, k) {
	const h = new MinHeap()
	nums.forEach((n) => {
		h.insert(n)
		// 当堆的大小超过k，就开始删除堆顶元素
		if (h.size() > k) {
			h.pop()
		}
	})
	// 堆顶元素就是第k个最大元素
	return h.peek()
}

leetCode 347.前k个高频元素

给定一个非空的整数数组，返回其中出现频率前k高的元素。

方法1:使用字典数据结构

const topK = function (nums, k) {
	const map = new Map()
	nums.foeEach((n) => {
		// 统计每个元素出现的频率
		map.set(n, map.has(n)?map.get(n) + 1, 1)
	})
	// 降序排序
	const list = Array.from(map).sort((a, b) => b[1] - a[1])
	
	// 返回前k个元素 
	return list.slice(0, k).map(n => n[0])
}	

方法2:

const topK = function (nums, k) {
}

leetCode 23.合并k个排序链表