一、线性
1、多项式
corrcoef函数
corrcoef函数用来计算矩阵相关系数。
(1)、corrcoef(x):若x为一个矩阵,返回的则是一个相关系数矩阵。
(2)、corrcoef(x,y):计算列向量x、y的相关系数,要求x、y具有相等的元素个数。如果x、y是矩阵,那么corrcoef函数会将其转换为列向量,相当于corrcoef([x(:),y(:)])。
p=polyfit(x,y,n)
[p,s]= polyfit(x,y,n)
说明:x,y为数据点,n为多项式阶数,返回p为幂次从高到低的多项式系数向量p。x必须是单调的。矩阵s用于生成预测值的误差估计。
多项式曲线求值函数:polyval( )
调用格式: y=polyval(p,x)
[y,DELTA]=polyval(p,x,s)
说明:y=polyval(p,x)为返回对应自变量x在给定系数P的多项式的值。
[y,DELTA]=polyval(p,x,s) 使用polyfit函数的选项输出s得出误差估计Y DELTA。它假设polyfit函数数据输入的误差是独立正态的,并且方差为常数。则Y DELTA将至少包含50%的预测值
利用matlab实现非线性拟合(三维、高维、参数方程)_matlab多元非线性拟合_hyhhyh21的博客-CSDN博客
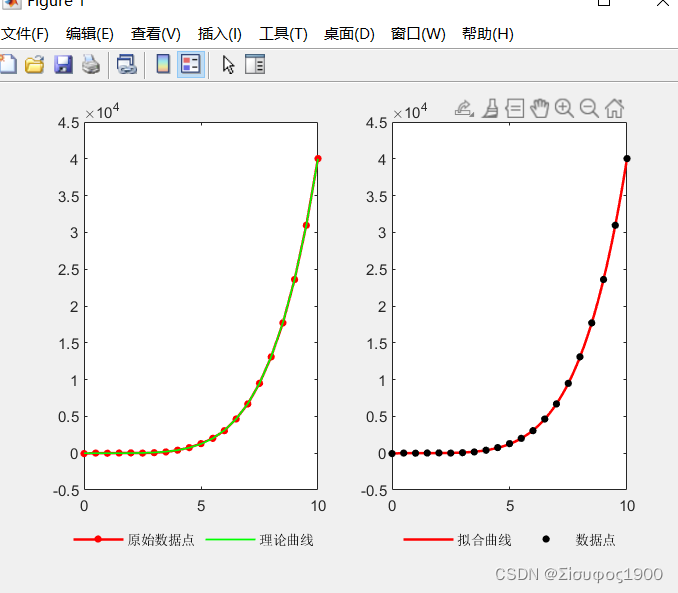
eg1:
y=0.4*x.^5+0.03*x.^4-0.5*x.^3+2.0*x.^2-0*x-4+100*(rand(size(x))-0.5); 原始函数
x=0:0.5:10;
y=0.4*x.^5+0.03*x.^4-0.5*x.^3+2.0*x.^2-0*x-4+100*(rand(size(x))-0.5); % 定义一个5阶的函数
p=polyfit(x,y,5); % 多项式拟合P的结果是系数 y=ax^5+bx^4+cx^3+dx^2 +ex+f n 表示的是阶数p =a b c d e f
x2=0:0.05:10;
y2=polyval(p,x2); % 将x 带入到polyfit 的系数中,计算出新的点
figure();
subplot(1,2,1)
hold on
plot(x,y,'linewidth',1.5,'MarkerSize',15,'Marker','.','color','r')
plot(x,0.4*x.^5+0.03*x.^4-0.5*x.^3+2.0*x.^2-0*x-4,'linewidth',1,'color','g')
hold off
legend('原始数据点','理论曲线','Location','southoutside','Orientation','horizontal')
legend('boxoff')
box on
subplot(1,2,2)
hold on
plot(x2,y2,'-','linewidth',1.5,'color','r')
plot(x,y,'LineStyle','none','MarkerSize',15,'Marker','.','color','k')
hold off
box on
legend('拟合曲线','数据点','Location','southoutside','Orientation','horizontal')
legend('boxoff')
eg2:
>> x = [0 10 20 30 40 50 60 70 80 90 100 110 120];
y = [5 1 7.5 3 4.5 8.8 15.5 6.5 -5 -10 -2 4.5 7 ];
>> matlab 9阶
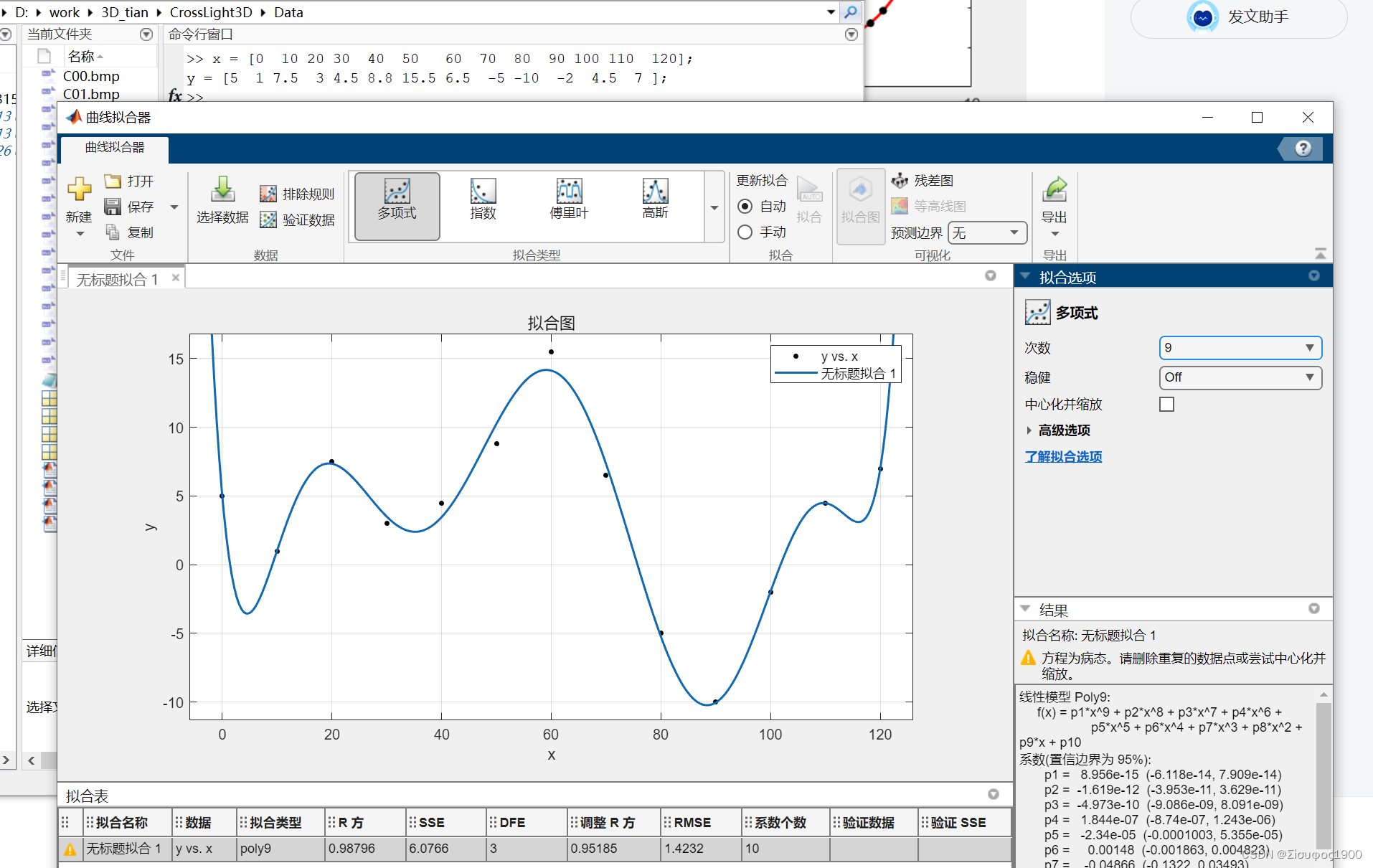
5阶
2、线性
Matlab 曲线拟合之 polyfit 、polyval、poly2str 函数_matlab poly2str_草帽当家de的博客-CSDN博客
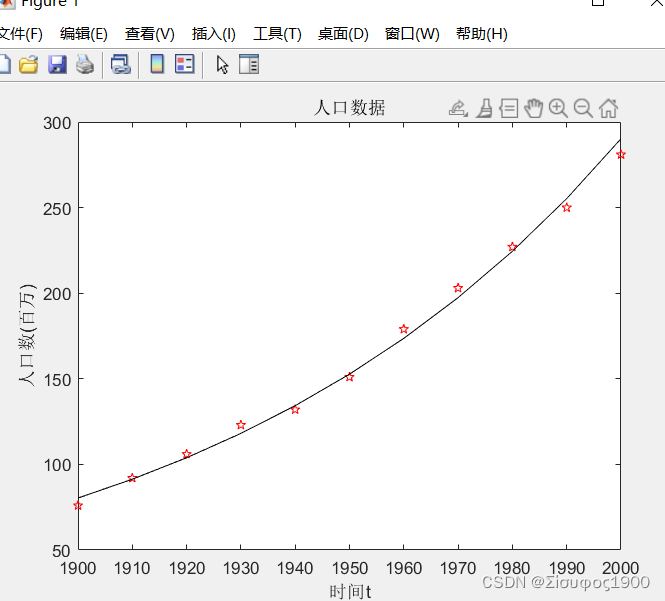
%线性
t = 1900:10:2000; %时间t
y = [76 92 106 123 132 151 179 203 227 250 281]; %人口y
yy = log(y); %指数基尼必需的线性化变形
p2 = polyfit(t,yy,1);% y=kx+b
b = p2(1);
a = exp(p2(2));
y2 = a * exp(b*t); %指数拟合函数式
plot(t,y,'rp',t,y2,'k-');
grid off;
xlabel('时间t');
ylabel('人口数(百万)');
title('人口数据');