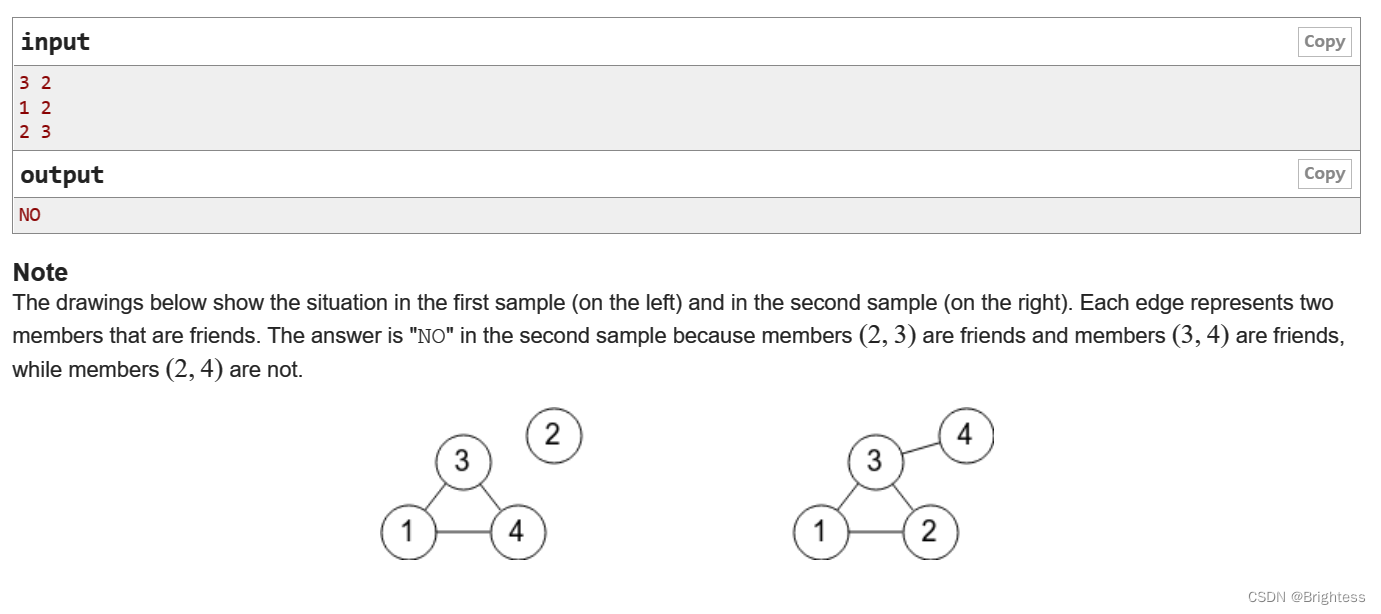
题目大意：

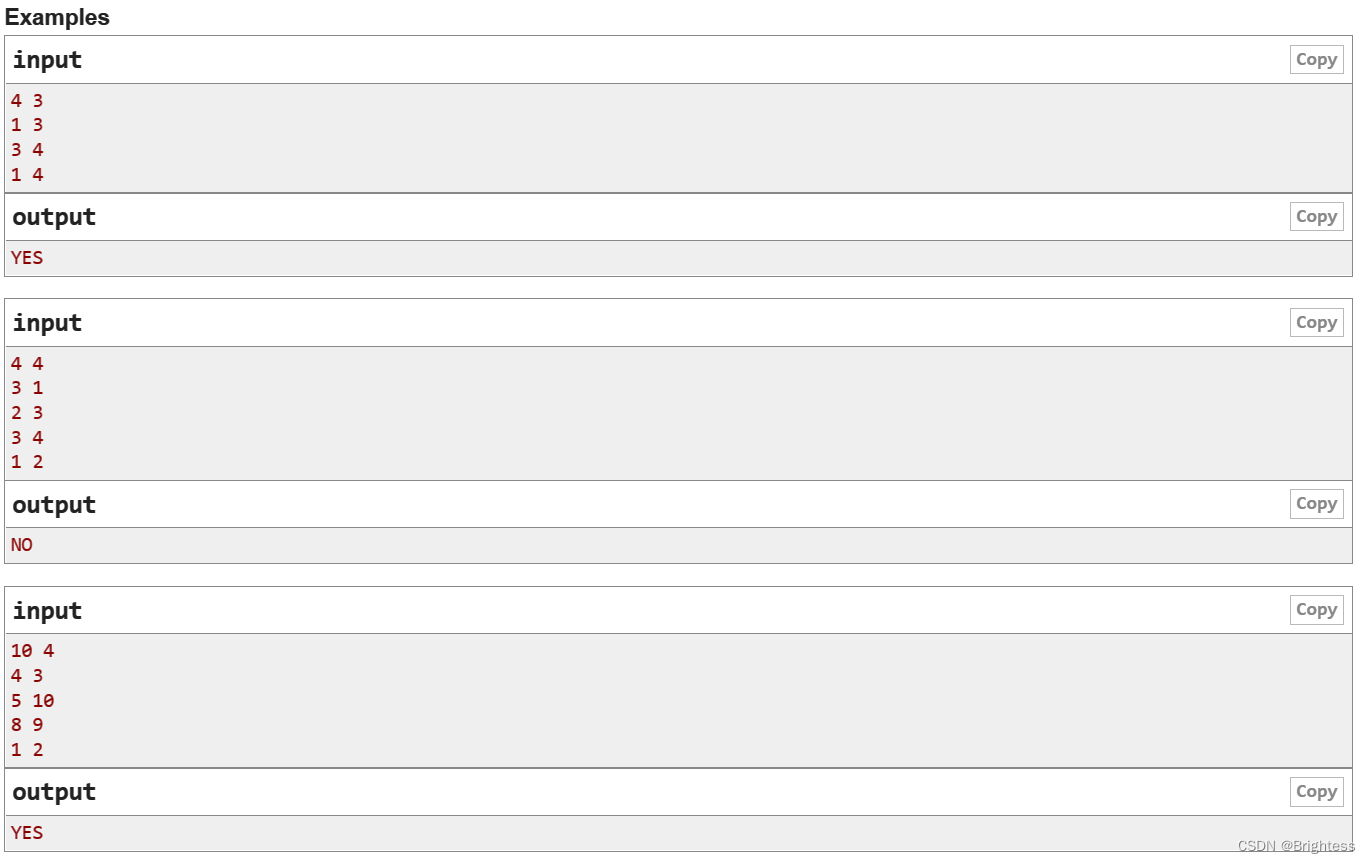
给你一些n个点m条边，如果三个点（a,b,c）是合法的，当且仅当 a-b,b-c,c-a都有一条边，问你这个图是否合法，如果有一个或两个点视为合法

思路

考虑什么图才是个合法图：除了点数小于 3 的图一定合法外，必须是完全图才合法，假设完全图有 n 个点，则它的边数为：(n - 1) * n / 2。

用并查集分割为若干个集合，dfs 遍历每个集合，判断每个大小大于2的图是否是完全图即可。

这里积累个小技巧，用set存图，每次操作 logn，方便统计图的边数，具体看代码。

时间复杂度：$O(nlogn)$

代码：

#include<bits/stdc++.h>

using namespace std;
#define int long long
const int N = 1.5e5 + 10;
int n, m;
int p[N], siz[N];
set<int> g[N];
int edge = 0;
bool vis[N];

int Find(int x) {
	if (p[x] != x) {
		p[x] = Find(p[x]);
	}
	return p[x];
}

void dfs(int u)
{
	vis[u] = true;
	edge += g[u].size();
	for (auto son : g[u]) {
		g[son].erase(u);
	}
	for (auto son : g[u]) {
		if (vis[son]) continue;
		dfs(son);
	}
}

signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	cin >> n >> m;
	for (int i = 1; i <= n; ++i) {
		p[i] = i;
		siz[i] = 1;
	}
	for (int i = 0; i < m; ++i) {
		int a, b; cin >> a >> b;
		g[a].insert(b);
		g[b].insert(a);
		int pa = Find(a), pb = Find(b);
		if (pa != pb) {
			siz[pb] += siz[pa];
			p[pa] = pb;
		}
	}
	for (int i = 1; i <= n; ++i) {
		p[i] = Find(i);
	}
	for (int i = 1; i <= n; ++i) {
		if (p[i] != i || siz[i] <= 2) continue;
		edge = 0;
		dfs(i);
		if (edge != siz[i] * (siz[i] - 1) / 2) {
			cout << "NO" << '\n';
			return 0;
		}
	}

	cout << "YES" << '\n';

	return 0;
}