2D-2D匹配: 对极几何
SLAM十四讲笔记1
1.1 对极几何數學模型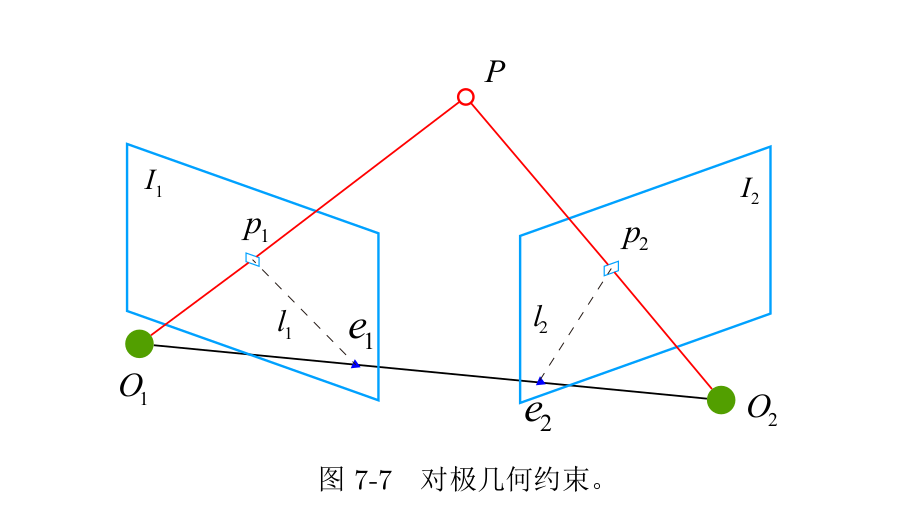
考虑从两张图像上观测到了同一个3D点,如图所示**。**我们希望可以求解相机两个时刻的运动 R , t R,t R,t。
假设我们要求取两帧图像 I 1 , I 2 I_1,I_2 I1,I2之间的运动,设第一帧到第二帧的运动为R ,t,两个相机中心分别为 O 1 , O 2 O_1,O_2 O1,O2.考虑 I 1 I_1 I1中有一个特征点 p 1 p_1 p1,它在 I 2 I_2 I2中对应着特征点 p 2 p_2 p2.连线$\overrightarrow{O_1 p_1} 和 和 和\overrightarrow{O_2 p_2}$ 在三维空间中交于点P,这时点 O 1 , O 2 , P O_1 ,O_2,P O1,O2,P三个点可以确定一个平面,为极平面. O 1 , O 2 O_1,O_2 O1,O2连线与像平面 I 1 , I 2 I_1,I_2 I1,I2的交点分别为 e 1 , e 2 e_1,e_2 e1,e2, e 1 , e 2 e_1,e_2 e1,e2称为极点, O 1 O 2 O_1O_2 O1O2称为基线,极平面与两个像平面 I 1 , I 2 I_1,I_2 I1,I2之间的相交线 l 1 , l 2 l_1,l_2 l1,l2称为极线.
P
P
P在
I
1
I_1
I1下的线号机坐标为
P
=
[
X
,
Y
,
Z
]
T
P=[X,Y,Z]^{T}
P=[X,Y,Z]T,两个投影像素点
p
1
,
p
2
p_1,p_2
p1,p2 的像素位置满足如下公式:
{
s
1
p
1
=
K
P
s
2
p
2
=
K
(
R
P
+
t
)
\left\{ \begin{aligned}s_1p_1 =KP\\ s_2p_2=K(RP+t)\\ \end{aligned} \right. \\\\
{s1p1=KPs2p2=K(RP+t)
取
p
1
,
p
2
p_1,p_2
p1,p2 的归一化坐标
{
x
1
=
K
−
1
p
1
x
2
=
K
−
1
p
2
\left\{\begin{aligned} x_{1} =K^{-1}p_1\\ x_{2} =K^{-1}p_2\\ \end{aligned}\right.
{x1=K−1p1x2=K−1p2
x 1 , x 2 x_1,x_2 x1,x2是两个像素归一化平面上的坐标。代入上式,得到 x 2 = R x 1 + t x_2=Rx_1 +t x2=Rx1+t
同时左乘
t
∧
t^{ ∧ }
t∧可得:
t
∧
x
2
=
t
∧
R
x
1
t^{ ∧ }x_2=t^{ ∧ }Rx_1
t∧x2=t∧Rx1
同时左乘
x
2
T
x^{T}_2
x2T,可得
x
2
T
t
∧
x
2
=
x
2
T
t
∧
R
x
1
x^{T}_2t^{ ∧ }x_2=x^{T}_2t^{ ∧ }Rx_1
x2Tt∧x2=x2Tt∧Rx1
可得
x
2
T
t
∧
R
x
1
=
0
x^{T}_2t^{ ∧ }Rx_1=0
x2Tt∧Rx1=0
重新带入
p
1
,
p
2
p_1,p_2
p1,p2,可得:
p
2
T
K
−
T
t
∧
R
K
−
1
p
1
=
0
p_2^{T}K^{-T}t^{ ∧ }RK^{-1}p_1=0
p2TK−Tt∧RK−1p1=0
以上俩个式子称为对极约束,定义基础矩阵F和本质矩阵E,可以进一步简化对极约束:
E
=
t
∧
R
F
=
K
−
T
E
K
−
1
x
2
T
E
x
1
=
p
2
T
F
p
1
=
0
E=t^{ ∧ }R \quad \quad \quad F=K^{-T}EK^{-1}\quad \quad \quad x^{T}_2Ex_1=p_2^{T}Fp_1=0
E=t∧RF=K−TEK−1x2TEx1=p2TFp1=0
本质矩阵E 的求解
考虑到E 的尺度等价性,可以用8对点来估计E,是为八点法.
对于一对匹配点,其归一化坐标
x
1
=
[
u
1
,
v
1
,
1
]
,
x
2
=
[
u
2
,
v
2
,
1
]
x_1=[u_1,v_1,1],x_2=[u_2,v_2,1]
x1=[u1,v1,1],x2=[u2,v2,1]根据对极约束,有
(
u
1
,
v
1
,
1
)
[
e
1
e
2
e
3
e
4
e
5
e
6
e
7
e
8
e
9
]
[
u
2
v
2
1
]
=
0
(u_1,v_1,1)\left[ \begin{matrix} e_1 &e_2 &e_3\\e_4 &e_5 &e_6 \\e_7 &e_8 &e_9 \end{matrix} \right]\left[ \begin{matrix} u_2\\v_2\\1\end{matrix} \right]=0
(u1,v1,1)
e1e4e7e2e5e8e3e6e9
u2v21
=0
把矩阵E展开为向量
[
e
1
e
2
e
3
e
4
e
5
e
6
e
7
e
8
e
9
]
T
\left[ \begin{matrix} e_1 &e_2 &e_3 &e_4 &e_5 &e_6 &e_7 &e_8 &e_9 \end{matrix} \right]^{T}
[e1e2e3e4e5e6e7e8e9]T ,对极约束可以写成与e ee有关的线性形式:
[
u
1
u
2
,
u
1
v
2
,
u
1
,
v
1
u
2
,
v
1
v
2
,
v
1
,
u
2
,
v
2
,
1
]
T
.
e
=
0
[u_1u_2,u_1v_2,u_1,v_1u_2,v_1v_2,v_1,u_2,v_2,1]^{T}.e=0
[u1u2,u1v2,u1,v1u2,v1v2,v1,u2,v2,1]T.e=0
把八对点对应的
x
1
,
x
2
x_1,x_2
x1,x2分别代入方程中,得到线性方程组:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-K9n4lOEh-1629730544222)(../AppData/Roaming/Typora/typora-user-images/1629650165462.png)]](https://img-blog.csdnimg.cn/f19e881aa226443cabb74e9d48548d2a.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0RhcmxpbmdxaWFuZw==,size_16,color_FFFFFF,t_70)
求得E后,对E进行SVD分解以求取R,t :设E的SVD分解为
E
=
U
∑
V
T
E=U \sum V^T
E=U∑VT则对应的R ,t 分别为:
t
∧
=
U
R
Z
(
π
2
)
∑
U
T
R
=
U
R
Z
T
(
π
2
)
∑
V
T
t^{∧} =U R_Z(\frac{\pi}{2})\sum U^T \quad \quad R=U R^{T}_Z(\frac{\pi}{2})\sum V^T
t∧=URZ(2π)∑UTR=URZT(2π)∑VT
其中
R
Z
(
π
2
)
R_Z(\frac{\pi}{2})
RZ(2π)表示沿Z轴旋转90°得到的旋转矩阵.
1.2 对极几何讨论
对极几何的讨论:
-
-
尺度不确定性: 2D图像不具有深度信息,这导致了单目视觉的尺度不确定性. 实践中设t 为单位1,计算相机运动和和特征点的3D位置,这被称为单目SLAM的初始化.
-
退化问题:当特征的共面或者相机发生纯旋转时,基础矩阵的自由度下降,就出现所谓的退化。实际中数据总是包含一些噪声,这时候继续使用八点法求解基础矩阵,基础矩阵多余出来的自由度将会主要由噪声决定。
为了可以避免退化现象造成的影响,通常在估计基础矩阵F的同时会求解单应矩阵H,选择重投影误差比较小的那个作为最终的运动估计矩阵。
-
初始化的纯旋转问题: 若相机发生纯旋转,导致t 为零,得到的E也将为零,会导致我们无从求解R.因此单目初始化不能只有纯旋转,必须要有一定程度的平移.
-
多于8对点的情况:
对于八点法,有 A e = 0 Ae=0 Ae=0,其中A为一个8×9的矩阵.
若匹配点的个数多于8个,A的尺寸变化,上述方程不成立.因此转而求取最小化二次型
m i n e ∣ ∣ A e ∣ ∣ 2 2 = m i n e e T A T A e min_e||Ae||^2_2=min_e e^TA^TAe mine∣∣Ae∣∣22=mineeTATAe
是为最小二乘意义下的E矩阵.1.3 E/F的意义
基础矩阵F描述了三维空间点P在摄像机不同方位下成像得到的投影像素点之间的关系。
本质矩阵E描述 相邻图像上对应像素归一化平面上的,估计相机在两个位置的相对运动。
-
1.4 SVD(奇异值分解)是一种常用的矩阵分解方法,其特点包括:
可以将任何矩阵分解成三个部分:左奇异矩阵、右奇异矩阵和奇异值矩阵。
-
奇异值矩阵是一个对角矩阵,其中的元素称为奇异值。奇异值是非负实数,代表着矩阵在每个主方向上的“重要程度”。
-
左奇异矩阵和右奇异矩阵都是正交矩阵。这意味着它们的转置矩阵等于它们的逆矩阵,所以可以用于矩阵的变换和逆变换。
-
SVD 分解可以用于数据降维、噪声滤波、图像压缩等领域,具有广泛的应用价值。
-
对于奇异值较小的部分可以进行截断操作,这可以有效地减少数据的维度并去除噪声。
-
SVD 分解是一种数值稳定的算法,能够处理大部分类型的矩阵并且不容易出现数值不稳定的情况。