人脸识别算法--非深度方法

在前深度学习时代，非深度的方法探索了不同的人脸识别算法。

先考虑一下非深度学习时代，人脸识别难在哪？或者说目标识别的难点在哪？

图像是一个高度冗余的数据。

* 图像数据中包含大量与语义无关的内容

* 图像数据中还包含大量噪声

所有的图像识别算法，都是在解决这个问题。

也就是说，如何从冗余的数据中，提取出关键的信息。

深度学习通过不断的卷积，越来越多的通道数量，以及大量的参数解决这个问题。

非深度方法如何处理？

PCA(主成分分析)

**动机**：

- 将高维特征映射到低维特征，减少计算复杂度和存储空间
- 从数据中提取最相关信息

**问题定义**：

将一个n维数据，映射到k维上。

**基本思想**：

什么才是最不冗余的坐标轴？

只有正交的坐标轴，才是最不冗余的。

因此，PCA的工作就是从原始空间中，顺序的找到一组组正交的坐标轴

例如，第一个坐标轴的选择，是原始数据中，方差最大的方向；

第二个坐标轴是与第一个坐标轴正交的平面中，方差最大的；依次类推。

最终，可以得到n个坐标轴。

我们可以发现一个问题：大部分的方差都集中在某几个维度中，其余维度的方差几乎没有。

因此，舍弃m个轴，保留方差最大的k个轴，从而实现对数据的降维。
**问题**：

如何得到包含最大差异的主成分方向？

**协方差矩阵**

协方差矩阵中，对角线位置是描述了每个维度本身的数据差异程度，而其余点则描述了不同维度之间的数据差异程度。
那么回顾一下我们的问题：如何找出数据的最大方差的方向？

也就是说，我们要把协方差矩阵进行降复杂度，也就是说，我们把里面一些数据轴删除以后(值为零)，这个矩阵和原来看起来差距不大。
**特征值分解**

特征值越大，重建出的矩阵为第一大主成分

**实现特征值分解：SVD**

PCA的直观感受

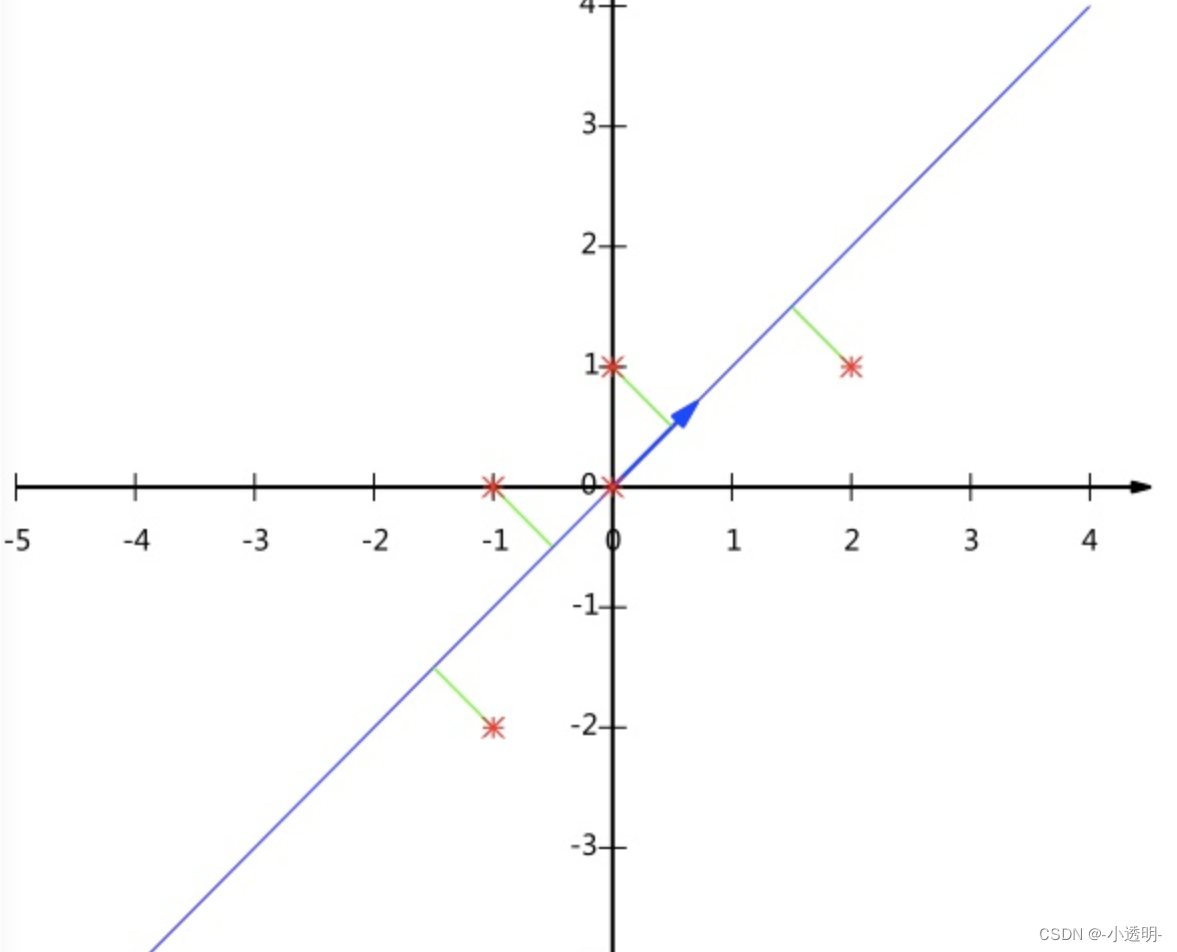
PCA的代码实现

import numpy as np

X = np.array([[-1, 1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
n_samples, n_features = X.shape
mean=np.array([np.mean(X[:,i]) for i in range(n_features)])
norm_X=X-mean
scatter_matrix=np.dot(np.transpose(norm_X),norm_X)
eig_val, eig_vec = np.linalg.eig(scatter_matrix)

print(eig_val)
print()
print(eig_vec)
eig_pairs = [(np.abs(eig_val[i]), eig_vec[:,i]) for i in range(n_features)]
eig_pairs.sort(reverse=True)
feature=np.array([ele[1] for ele in eig_pairs[:1]])
print(feature)
data=np.dot(norm_X,np.transpose(feature))
print(data)