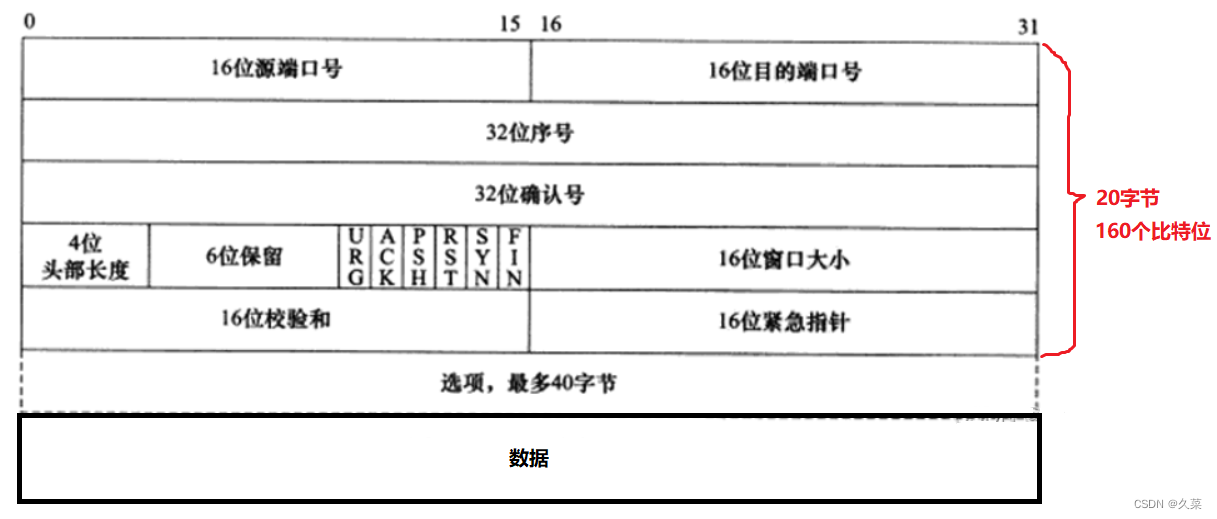
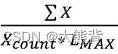问题描述：

迪杰斯特拉算法
Time Limit: 2000 MS		Memory Limit: 5000 KB

Description

给定n(n<=500)个顶点,以及E(E<=10000)条边，使用迪杰斯特拉算法计算顶点s到顶点t的最短路径.

Input

第一行输入T表示有T组数据。每组数据第一行输入n、E、s、t，分别表示顶点数、边数、顶点s以及顶点t. 接下来
输入E行每行三个正整数u(1<=u<=n)、v(1<=v<=n)、w，表示顶点u到顶点v之间无向边长度w（可能有重边）。

Output

输出T行正整数，第i行表示第i组数据s到达t的最短路径长度。若s无法到达t国，输出-1.

Sample Input

Sample Output

1
-1
2

问题分析：

狄克斯特拉算法 是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。

可以使用两个数组，一个记录是否已经找到最短路径，另一个用于记录找到的最短路径值，

代码示例：

#include <iostream>
#include <cstring>
using namespace std;

const int N = 510, M = 10010, INF = 0x3f3f3f3f;

int n, m, s, t;
int h[N], e[M], w[M], ne[M], idx; // 邻接表存储图
int dist[N]; // dist[i] 表示起点到 i 的最短距离
bool st[N]; // st[i] 表示 i 是否已经确定了最短路

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++; // 添加一条从 a 到 b 权值为 c 的边
}

int dijkstra() {
    memset(dist, 0x3f, sizeof dist); // 将 dist 数组全部初始化为 INF，表示起点到所有点的距离都未知
    dist[s] = 0; // 起点到自身的距离为 0
    for (int i = 0; i < n; i++) { // 迭代 n 次，每次确定一个最短路
        int t = -1; // t 记录还未确定最短路的点中，离起点最近的点
        for (int j = 1; j <= n; j++) // 找离起点最近的点
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
        st[t] = true; // 标记 t 已经确定了最短路
        for (int j = h[t]; ~j; j = ne[j]) { // 用 t 更新其他点的距离
            int k = e[j];
            if (dist[k] > dist[t] + w[j])
                dist[k] = dist[t] + w[j];
        }
    }
    if (dist[t] == INF) return -1; // t 不可达，返回 -1
    else return dist[t]; // 返回起点到 t 的最短距离
}

int main() {
    int T;
    cin >> T;
    while (T--) {
        cin >> n >> m >> s >> t;
        memset(h, -1, sizeof h);
        idx = 0;
        for (int i = 0; i < m; i++) {
            int a, b, c;
            cin >> a >> b >> c;
            add(a, b, c), add(b, a, c); // 添加一条无向边
        }
        cout << dijkstra() << endl;
    }
    return 0;
}