前言

Sqrt Decomposition 是一种数据结构，能够在O(1)时间复杂度内完成数组元素值的查询和更新，在$O(\sqrt{n})$ 时间复杂度内完成数组某个区间属性值的查询和批量更新某个区间的值。这里的属性 可以是区间的和、最小值、最大值等。

说到区间的和，你可能会想到前缀和，能够在O(1)时间复杂度内查询区间的和，明显比本文要说的Sqrt Decomposition 更快。但是它不支持数据的更新，因为更新后需要重新计算前缀和。

Sqrt Decomposition 来自于分块思想的启发，把数组分成若干的长度相等的区块（最后一块除外）。区块长度可以任取，但一般为数组长度取根号。 假设我们有一个数组$a[\mathrm{0...}n-1]$, 那么区块长度$s=\lceil \sqrt{n}\rceil$。如图：

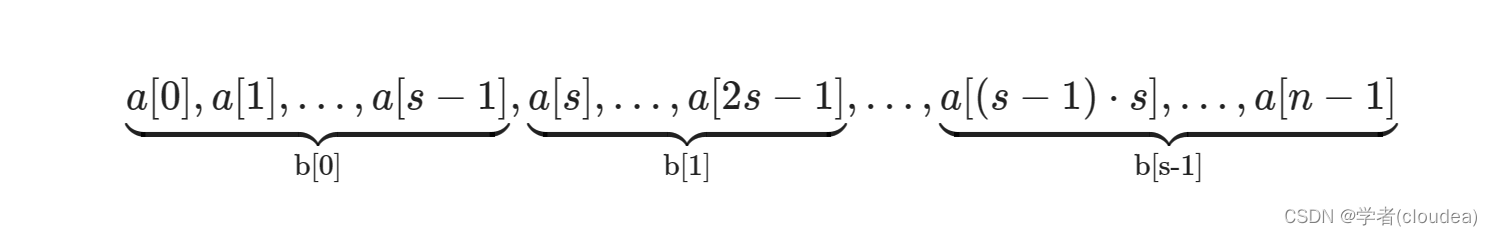
以计算区间和为例。引入数组$b[\mathrm{0...}s-1]$ ，其中$b[j]$表示第$j$个区块的和。这时：

• 当获取数组位置$i$某个值时，直接读取$a[i]$即可。
• 当设置数组位置$i$某个值$v$时，更新$b[j]=b[j]+v-a[i]$，再直接设置$a[i]$即可。
• 查询区间$[l,r]$的和时，区间被分为三个部分：
  • 对于开头不完整区块，逐个累加。
  • 对于中间完整区块，累加对应b中的值
  • 对于结尾不完整区块，逐个累加。

对于前两种操作，显然$O(1)$时间即可完成。
对于最后一种操作，时间复杂度计算如下：
$$\begin{array}{rl}T(n)& =左区间累加次数+中间完整区间数+右区间累加次数\\ & \le s+s+s\\ & =O(\sqrt{n})\end{array}$$

到目前为上，还不支持区间的批量更新。即把区间的值同时加上某一个值，例如[l, r]范围内的值，同时加上5。如果把批量更新拆解成对数组a中[l, r]范围内每个元素的更新，则复杂度为O(n), 太高了。因此需要额外引入数组$c[\mathrm{0...}s-1]$记录区间的更新。更新过程如下，依然是把区间分为三个部分：

• 对于开头不完整区块，逐个更新值到数组a
• 对于中间完整区块，把更新记录对应区块中的c中的值
• 对于结尾不完整区块，逐个更新值到数组a。

与计算区间和方法一样，可以计算这样操作的时间复杂度为$O(\sqrt{n})$。

因为有部分更新是记录到c中，所以逻辑上数组第$i$个位置的值应由a和c共同组成。即 $data[i]=a[i]+c[j]/s$ 。其中$j$表示数组第$i$个位置对应的区块索引号。

参考：
https://cp-algorithms.com/data_structures/sqrt_decomposition.html#description

实现

以go语言，实现上述区间和的例子。

package main

import (
	"fmt"
	"math"
)

type SqrtDecomposition struct {
	a []int
	s int   // 区间长度
	b []int // 区间和
	c []int // 区间delta。data[i] = a[i] + c[j] / s
}

func NewSqrtDecomposition(data []int) *SqrtDecomposition {
	// 初始化分区大小
	s := 2
	if len(data) > 4 {
		s = int(math.Ceil(math.Sqrt(float64(len(data)))))
	}
	// 分区个数
	count := 1 + (len(data)-1)/s

	// 计算b[i] 和 c[i]值
	// b[i] 即表示小区间的和。遍历相加即可
	// c[i] 初始值为0
	b := make([]int, count)
	c := make([]int, count)
	for i := 0; i < len(data); i++ {
		b[i/s] += data[i]
	}

	// 计算c[i] 值
	return &SqrtDecomposition{
		a: data,
		s: s,
		b: b,
		c: c,
	}
}

/*
*
获取某个位置的区间号和区间长度
*/
func (receiver *SqrtDecomposition) getInfo(p int) (int, int) {
	le := receiver.s
	no := p / le
	if no == len(receiver.b)-1 {
		le = len(receiver.a) - no*le
	}
	return no, le
}

/*
*
获取数组长度
*/
func (receiver *SqrtDecomposition) Size() int {
	return len(receiver.a)
}

/*
*
获取范围内的和
*/
func (receiver *SqrtDecomposition) GetRange(l int, r int) int {
	sum := 0
	i := l
	for i <= r {
		if i%receiver.s == 0 && (i+receiver.s-1) <= r {
			no, _ := receiver.getInfo(i)
			sum += receiver.b[no]
			i += receiver.s
		} else {
			sum += receiver.Get(i)
			i += 1
		}
	}
	return sum
}

/*
*
获取第p个位置的值
*/
func (receiver *SqrtDecomposition) Get(p int) int {
	no, le := receiver.getInfo(p)
	return receiver.a[p] + receiver.c[no]/le
}

/*
*
设置第p个位置的值
*/
func (receiver *SqrtDecomposition) Set(p int, v int) {
	no, le := receiver.getInfo(p)
	newAi := v - receiver.c[no]/le
	receiver.b[no] += newAi - receiver.a[p]
	receiver.a[p] = newAi
}

/*
*
给一定范围内的值增加一个变化
*/
func (receiver *SqrtDecomposition) SetRange(l int, r int, d int) {
	i := l
	for i <= r {
		if i%receiver.s == 0 && (i+receiver.s-1) <= r {
			no, _ := receiver.getInfo(i)
			receiver.c[no] += d * receiver.s
			receiver.b[no] += d * receiver.s
			i += receiver.s
		} else {
			receiver.Set(i, receiver.Get(i)+d)
			i += 1
		}
	}
}

测试

对各个功能进行了测试，测试结果与代码如下：

func main() {
	structure := NewSqrtDecomposition([]int{
		1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
	})

	//get
	fmt.Println("【初始值】")
	fmt.Print("值：")
	for i := 0; i < structure.Size(); i++ {
		fmt.Print(structure.Get(i), " ")
	}
	fmt.Println()
	fmt.Print("和：")
	for i := 0; i < len(structure.b); i++ {
		fmt.Print(structure.b[i], " ")
	}
	fmt.Println()

	// set
	for i := 0; i < structure.Size(); i++ {
		structure.Set(i, structure.Size()-i)
	}
	fmt.Println("【设置后的值】")
	fmt.Print("值：")
	for i := 0; i < structure.Size(); i++ {
		fmt.Print(structure.Get(i), " ")
	}
	fmt.Println()
	fmt.Print("和：")
	for i := 0; i < len(structure.b); i++ {
		fmt.Print(structure.b[i], " ")
	}
	fmt.Println()

	// get range
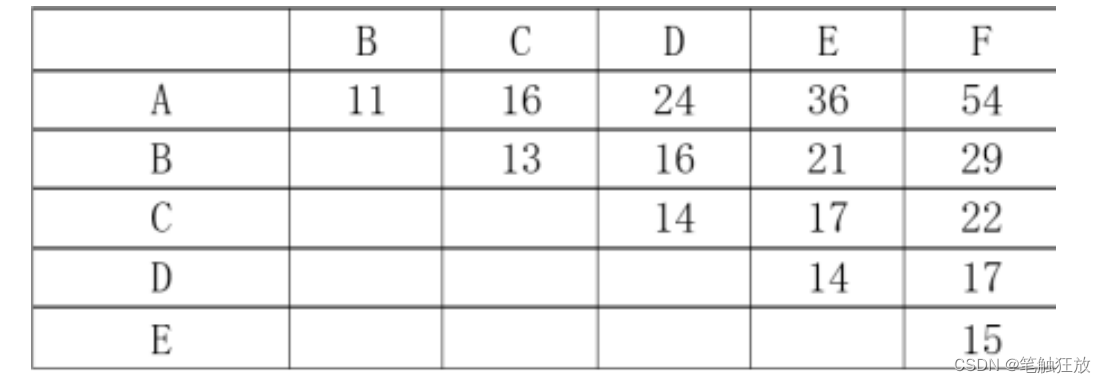
	fmt.Println("【获取范围】")
	for i := 0; i < structure.Size(); i++ {
		for j := 0; j < structure.Size(); j++ {
			if j >= i {
				fmt.Print(structure.GetRange(i, j), "\t")
			} else {
				fmt.Print("-", "\t")
			}
		}
		fmt.Println()
	}

	// set range
	structure.SetRange(1, 8, 2)
	structure.SetRange(5, 9, -3)

	fmt.Println("【设置范围】")
	fmt.Print("值：")
	for i := 0; i < structure.Size(); i++ {
		fmt.Print(structure.Get(i), " ")
	}
	fmt.Println()
	fmt.Print("和：")
	for i := 0; i < len(structure.b); i++ {
		fmt.Print(structure.b[i], " ")
	}
	fmt.Println()
	for i := 0; i < structure.Size(); i++ {
		for j := 0; j < structure.Size(); j++ {
			if j >= i {
				fmt.Print(structure.GetRange(i, j), "\t")
			} else {
				fmt.Print("-", "\t")
			}
		}
		fmt.Println()
	}
	fmt.Println()
}