文章目录
- 说明
- day41 顺序查找与折半查找
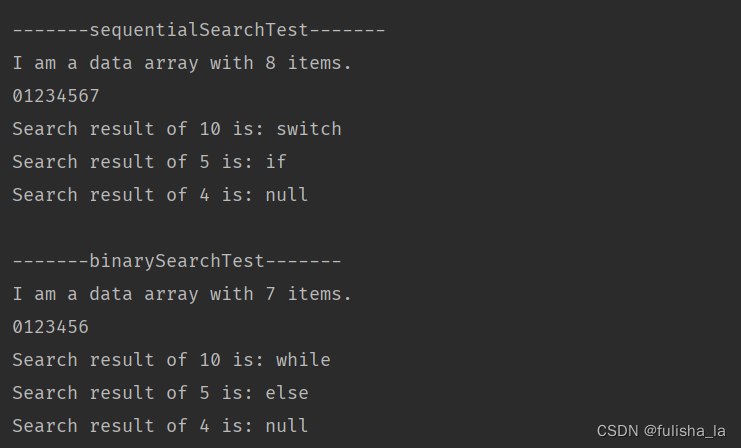
- 1.顺序查找
- 2.折半查找
- 3.代码
说明
闵老师的文章链接: 日撸 Java 三百行(总述)_minfanphd的博客-CSDN博客
自己也把手敲的代码放在了github上维护:https://github.com/fulisha-ok/sampledata
day41 顺序查找与折半查找
1.顺序查找
从线性表的一边开始,逐个检查每个关键字是否满足条件。在顺序查中,引入了一个哨兵,他的作用:在数组0索引处存放我们需要查询的数据,引入哨兵的好处是在循环的过程中不用判断数组是否越界,因为当i==0时,循环一定会跳出。哨兵主要作用就是可以避免我们进行不必要的判断,借助这个思想在其他算法中也可以引入哨兵。
时间复杂度
- 最好情况
若第一个数据就是我们要查找的数据,则时间复杂度可以是O(1) - 最坏情况
若最后一个数据或者我们查找的数据没在数组中,则需要遍历所以数据(一个for循环), 则时间复杂度可以是O(n) - 平均
综合最好和最坏,则时间复杂度是O(n)
2.折半查找
一般的顺序查找是无序的,而折半查找 他主要适用的是有序的顺序查找,
思路:(假设顺序有升序排列)
- 1.key值和中间位置的关键字比较,若相等查找成功
- 2.若不相等,key值大于中间元素关键字,则查找元素可能在后半部分;若key值小于中间元素,则查找元素可能在前半部分。则缩小范围内查询
- 对于折半查找我让我联想的到二叉排序树,二叉排序树的查找和二分查找很相似,但是二分查找他适用于有序的顺序表,而二叉排序树是树,有顺序存储和链式存储,之前在day22中给出的一种存储是压缩存储,所以二叉排序树的查找与二分查找的实现,还是要结合具体的存储结构
时间复杂度
- 最好情况
若第一个数据就是我们要查找的数据,则时间复杂度可以是O(1) - 最坏情况
若最后一个数据或者我们查找的数据没在数组中,则需要需要进行 log n 次比较。所以折半查找的最坏时间复杂度为 O(log n)。 - 平均
综合最好和最坏,则时间复杂度是 O(log n)
顺序查找在最坏情况下需要将数组中所有的数据都遍历完,而折半查找每一次查找都会将待查找的元素范围缩小到一半,所以折半查找的时间复杂度要比顺序查找低。
3.代码
package graph;
import datastructure.queue.CircleObjectQueue;
import datastructure.stack.ObjectStack;
public class AdjacencyList {
/**
* An inner class for adjacent node.
*/
class AdjacencyNode {
/**
* The column index.
*/
int column;
/**
* The next adjacent node.
*/
AdjacencyNode next;
/**
* The first constructor.
*
* @param paraColumn
*/
public AdjacencyNode(int paraColumn) {
column = paraColumn;
next = null;
}
}
int numNodes;
AdjacencyNode[] headers;
public AdjacencyList(int[][] paraMatrix) {
numNodes = paraMatrix.length;
// Step 1. Initialize. The data in the headers are not meaningful.
AdjacencyNode tempPreviousNode, tempNode;
headers = new AdjacencyNode[numNodes];
for (int i = 0; i < numNodes; i++) {
headers[i] = new AdjacencyNode(-1);
tempPreviousNode = headers[i];
for (int j = 0; j < numNodes; j++) {
if (paraMatrix[i][j] == 0) {
continue;
}
tempNode = new AdjacencyNode(j);
tempPreviousNode.next = tempNode;
tempPreviousNode = tempNode;
}
}
}
@Override
public String toString() {
String resultString = "";
AdjacencyNode tempNode;
for (int i = 0; i < numNodes; i++) {
tempNode = headers[i].next;
while (tempNode != null) {
resultString += " (" + i + ", " + tempNode.column + ")";
tempNode = tempNode.next;
} // Of while
resultString += "\r\n";
}
return resultString;
}
boolean[] tempVisitedArray;
String resultString = "";
public String breadthFirstTraversal(int paraStartIndex) {
CircleObjectQueue tempQueue = new CircleObjectQueue();
String resultString = "";
tempVisitedArray = new boolean[numNodes];
tempVisitedArray[paraStartIndex] = true;
// Initialize the queue.
// Visit before enqueue.
tempVisitedArray[paraStartIndex] = true;
resultString += paraStartIndex;
tempQueue.enqueue(new Integer(paraStartIndex));
// Now visit the rest of the graph.
int tempIndex;
Integer tempInteger = (Integer) tempQueue.dequeue();
AdjacencyNode tempNode;
while (tempInteger != null) {
tempIndex = tempInteger.intValue();
// Enqueue all its unvisited neighbors. The neighbors are linked
// already.
tempNode = headers[tempIndex].next;
while (tempNode != null) {
if (!tempVisitedArray[tempNode.column]) {
// Visit before enqueue.
tempVisitedArray[tempNode.column] = true;
resultString += tempNode.column;
tempQueue.enqueue(new Integer(tempNode.column));
} // Of if
tempNode = tempNode.next;
} // Of for i
// Take out one from the head.
tempInteger = (Integer) tempQueue.dequeue();
} // Of while
return resultString;
}
public String depthFirstTraversal(int paraStartIndex) {
ObjectStack tempStack = new ObjectStack();
resultString = "";
tempVisitedArray = new boolean[numNodes];
tempVisitedArray[paraStartIndex] = true;
resultString += paraStartIndex;
tempStack.push(new Integer(paraStartIndex));
System.out.println("Push " + paraStartIndex);
System.out.println("Visited " + resultString);
int tempIndex = paraStartIndex;
int tempNext;
Integer tempInteger;
AdjacencyNode tempNode;
while (true) {
tempNext = -1;
// Find an unvisited neighbor and push
tempNode = headers[tempIndex].next;
while (tempNode != null) {
if (!tempVisitedArray[tempNode.column]) {
// Visit before enqueue.
tempVisitedArray[tempNode.column] = true;
resultString += tempNode.column;
tempStack.push(new Integer(tempNode.column));
System.out.println("Push " + tempNode.column);
tempNext = tempNode.column;
break;
} // Of if
tempNode = tempNode.next;
}
if (tempNext == -1) {
//there is no neighbor node, pop
tempInteger = (Integer) tempStack.pop();
System.out.println("Pop " + tempInteger);
if (tempStack.isEmpty()) {
//No unvisited neighbor。Backtracking to the last one stored in the stack
break;
} else {
tempInteger = (Integer) tempStack.pop();
tempIndex = tempInteger.intValue();
tempStack.push(tempInteger);
}
} else {
tempIndex = tempNext;
}
}
return resultString;
}
public boolean breadthTraversal(int paraStartIndex) {
tempVisitedArray = new boolean[numNodes];
resultString = "";
breadthFirstTraversal(paraStartIndex);
for (int i = 0; i < numNodes; i++){
if (!tempVisitedArray[i]){
breadthFirstTraversal(i);
return false;
}
}
return true;
}
public boolean depthTraversal(int paraStartIndex){
tempVisitedArray = new boolean[numNodes];
resultString = "";
depthFirstTraversal(paraStartIndex);
for (int i = 0; i < numNodes; i++){
if (!tempVisitedArray[i]){
depthFirstTraversal(i);
return false;
}
}
return true;
}
public static void breadthFirstTraversalTest() {
// Test an undirected graph.
//int[][] tempMatrix = { { 0, 1, 1, 0 }, { 1, 0, 0, 1 }, { 1, 0, 0, 0}, { 0, 1, 0, 0} };
//int[][] tempMatrix = { { 0, 1, 1, 0 , 0}, { 1, 0, 0, 1, 0 }, { 1, 0, 0, 1, 0}, { 0, 1, 1, 0, 0}, { 0, 0, 0, 0, 0} };
int[][] tempMatrix = { { 0, 1, 1, 0 , 0, 0, 0}, { 1, 0, 0, 1, 0, 0, 0 }, { 1, 0, 0, 1, 0, 0, 0}, { 0, 1, 1, 0, 0, 0, 0}, { 0, 0, 0, 0, 0, 1, 1}, { 0, 0, 0, 0, 1, 0, 0}, { 0, 0, 0, 0, 0, 0, 0} };
Graph tempGraph = new Graph(tempMatrix);
System.out.println(tempGraph);
AdjacencyList tempAdjList = new AdjacencyList(tempMatrix);
String tempSequence = "";
try {
// tempSequence = tempAdjList.breadthFirstTraversal(2);
tempGraph.breadthTraversal(0);
} catch (Exception ee) {
System.out.println(ee);
} // Of try.
System.out.println("The breadth first order of visit: " + tempGraph.resultString);
}
public static void depthFirstTraversalTest() {
// Test an undirected graph.
//int[][] tempMatrix = { { 0, 1, 1, 0 }, { 1, 0, 0, 1 }, { 1, 0, 0, 0}, { 0, 1, 0, 0} };
// int[][] tempMatrix = { { 0, 1, 1, 0 , 0}, { 1, 0, 0, 1, 0 }, { 1, 0, 0, 1, 0}, { 0, 1, 1, 0, 0}, { 0, 0, 0, 0, 0} };
int[][] tempMatrix = { { 0, 1, 1, 0 , 0, 0, 0}, { 1, 0, 0, 1, 0, 0, 0 }, { 1, 0, 0, 1, 0, 0, 0}, { 0, 1, 1, 0, 0, 0, 0}, { 0, 0, 0, 0, 0, 1, 1}, { 0, 0, 0, 0, 1, 0, 0}, { 0, 0, 0, 0, 0, 0, 0} };
Graph tempGraph = new Graph(tempMatrix);
System.out.println(tempGraph);
AdjacencyList tempAdjList = new AdjacencyList(tempMatrix);
String tempSequence = "";
try {
tempGraph.depthTraversal(0);
// tempSequence = tempAdjList.depthFirstTraversal(2);
} catch (Exception ee) {
System.out.println(ee);
} // Of try.
System.out.println("The depth first order of visit: " + tempGraph.resultString);
}
public static void main(String args[]) {
int[][] tempMatrix = { { 0, 1, 0 }, { 1, 0, 1 }, { 0, 1, 0 } };
AdjacencyList tempTable = new AdjacencyList(tempMatrix);
System.out.println("The data are:\r\n" + tempTable);
breadthFirstTraversalTest();
depthFirstTraversalTest();
}
}