一、题目
1、题目描述
给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
示例1:
输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出:6
解释:最大矩形如上图所示。
示例2:
输入:matrix = []
输出:0
示例3:
输入:matrix = [["0"]]
输出:0
示例4:
输入:matrix = [["1"]]
输出:1
示例5:
输入:matrix = [["0","0"]]
输出:0
2、基础框架
class Solution {
public:
int maximalRectangle(vector<vector<char>>& matrix) {
}
};
3、原题链接
Leetcode 85. 最大矩形
二、解题报告
1、思路分析
(1)暴力解法
n
∗
n
n*n
n∗n 的矩阵中的子矩阵个数为
n
4
n ^4
n4,因为在
n
∗
n
n * n
n∗n 的矩阵中,随便选择一个点作为点 A 的选法有
n
2
n ^2
n2 种,随便选择一个点作为点 B 的选法有
n
2
n ^2
n2 种,而 A 和 B 一个作为左上角,一个作为右下角,可以得到一个矩形,可能有重复的,但是没有关系,所以得到子矩阵的个数为
n
2
∗
n
2
=
n
4
n ^ 2 * n^2 = n ^4
n2∗n2=n4 。
暴力解就是 4 重 for 循环枚举出每个子矩阵,然后再 2 重 for 循环验证该子矩阵中是不是每个位置都是 1,所以总的时间复杂度是 O ( n 6 ) O(n ^6) O(n6)。
(2)非暴力解法
例子:
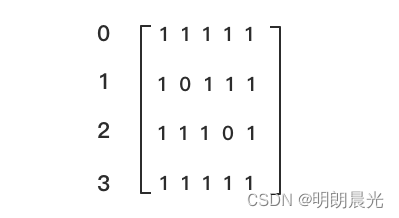
先求子矩阵必须以第 0 行作为地基的情况下,哪个子矩阵包含的 1 最多,即将其作为直方图考虑

然后求必须以第 1 行作为地基,第 1 行的高度压到第 0 行上,遇到 0 的情况,将高度处理为0。这是数组压缩 技巧:
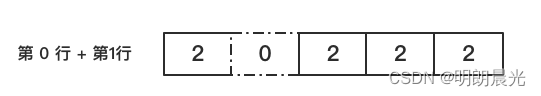
然后求必须以第 2 行作为地基,第 2 行压到之前的高度上,同样地,遇到 0 时,将高度处理为 0,将得到如下的结果:

最后必须以第 3 行作为地基,第 3 行压到之前的高度上:

这就得到了必须以第 3 行作为地基的情况下的子数组。
客观上,最大矩形肯定是以某一行作为地基的,上面的流程就列举了所有的可能性。
每一行处理都需要用到单调栈:压缩后的数组以每个位置为矩形的高度可能扩充的范围。
每一行处理的时间复杂度为 O ( n ) O(n) O(n),一共 n n n 行需要处理,所以总的时间复杂度就是 O ( n 2 ) O(n^2) O(n2)。
2、时间复杂度
O ( n 2 ) O(n^2) O(n2)
3、代码详解
C++ 版
- 不使用系统stack版
class Solution {
public:
int maximalRectangle(vector<vector<char>>& matrix) {
if (matrix.size() == 0 || matrix[0].size() == 0)
return 0;
//压缩数组得到直方图数组
int row = matrix.size();
int col = matrix[0].size();
int heights[col];
memset(heights, 0, sizeof(heights));
int ans = 0;
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
heights[j] = matrix[i][j] == '0' ? 0 : heights[j] + 1;
}
ans = max(ans, maxRectangle(heights, col));
}
return ans;
}
//对每一行处理得到的直方图都用单调栈求解最大矩形
int maxRectangle(int *heights, int col) {
int _stack[col];
memset(_stack, 0, sizeof(_stack));
int si = -1;
int ans = 0;
for (int i = 0; i < col; i++) {
while (si != -1 && heights[_stack[si]] >= heights[i]) {
int cur = heights[_stack[si--]];
int left = si == -1 ? -1 : _stack[si];
int area = cur * (i - left - 1);
ans = max(ans, area);
}
_stack[++si] = i;
}
while (si != -1) {
int cur = heights[_stack[si--]];
int left = si == -1 ? -1 : _stack[si];
int area = cur * (col - left - 1);
ans = max(ans, area);
}
return ans;
}
};
- 使用系统stack版
class Solution {
public:
int maximalRectangle(vector<vector<char>>& matrix) {
if (matrix.size() == 0 || matrix[0].size() == 0) return 0;
int row = matrix.size();
int col = matrix[0].size();
int ans = 0;
//准备一个直方图数组
int heights[col];
memset(heights, 0, sizeof(heights));
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
heights[j] = matrix[i][j] == '0' ? 0 : heights[j] + 1;
}
ans = max(ans, maxRecFromBottom(heights, col));
}
return ans;
}
int maxRecFromBottom(int *heights, int len) {
if (len == 0) return 0;
int area = 0;
stack<int> sta;
for (int i = 0; i < len; i++) {
while (!sta.empty() && heights[sta.top()] >= heights[i]) {
int j = sta.top();
sta.pop();
int k = sta.empty() ? -1 : sta.top();
area = max(area, (i - k - 1) * heights[j]);
}
sta.push(i);
}
while (!sta.empty()) {
int j = sta.top();
sta.pop();
int k = sta.empty() ? -1 : sta.top();
int curArea = (len - k - 1) * heights[j];
area = max(area, curArea);
}
return area;
}
};
Java 版
public class Code04_MaximalRectangle {
public static int maximalRectangle(char[][] map) {
if (map == null || map.length == 0 || map[0].length == 0) {
return 0;
}
int maxArea = 0;
int[] height = new int[map[0].length]; //准备一个直方图数组
//处理得到直方图数组
for (int i = 0; i < map.length; i++) {
for (int j = 0; j < map[0].length; j++) {
height[j] = map[i][j] == '0' ? 0 : height[j] + 1;
}
maxArea = Math.max(maxRecFromBottom(height), maxArea); //对每一行处理得到的直方图都用单调栈求解
}
return maxArea;
}
// height是直方图数组
public static int maxRecFromBottom(int[] height) {
if (height == null || height.length == 0) {
return 0;
}
int maxArea = 0;
Stack<Integer> stack = new Stack<Integer>();
for (int i = 0; i < height.length; i++) {
while (!stack.isEmpty() && height[i] <= height[stack.peek()]) {
int j = stack.pop();
int k = stack.isEmpty() ? -1 : stack.peek();
int curArea = (i - k - 1) * height[j];
maxArea = Math.max(maxArea, curArea);
}
stack.push(i);
}
while (!stack.isEmpty()) {
int j = stack.pop();
int k = stack.isEmpty() ? -1 : stack.peek();
int curArea = (height.length - k - 1) * height[j];
maxArea = Math.max(maxArea, curArea);
}
return maxArea;
}
}











![[附源码]计算机毕业设计springboot课室预约系统](https://img-blog.csdnimg.cn/2237d3eec6c243ea81843afe77282265.png)