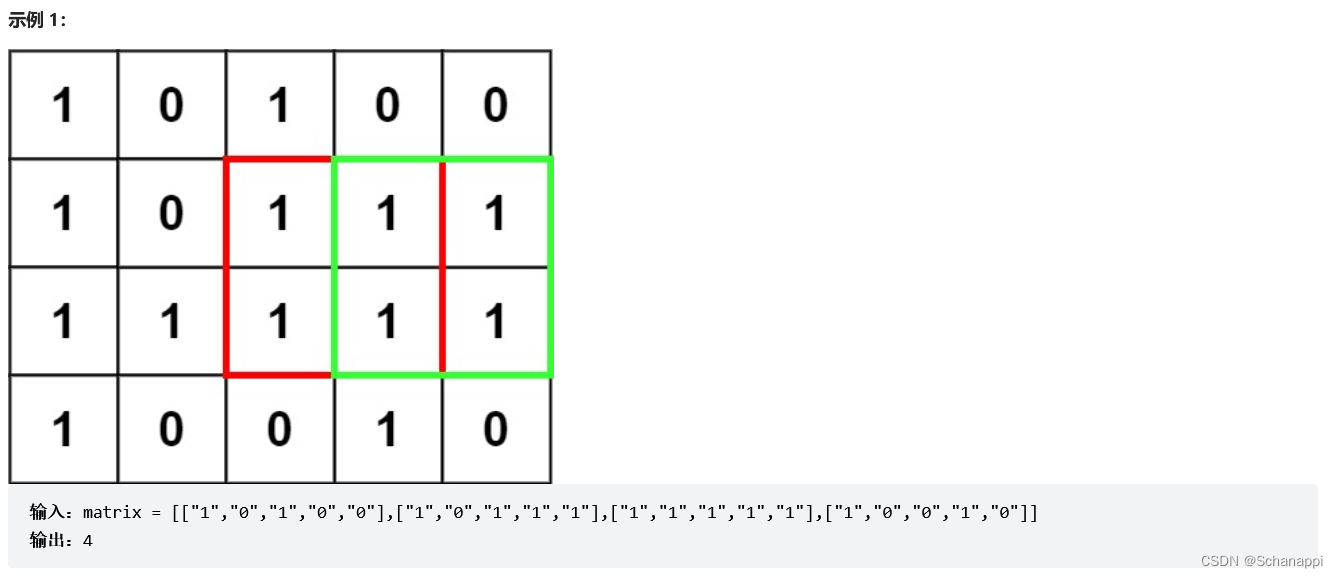
221.最大正方形（中等）

1. 题解

   • 对于在矩阵内搜索正方形或长方形的题型，一种常见的做法是：定义一个二维 dp 数组，其中 dp[i][j] 表示满足题目条件的、以（i,j）为右下角的正方形或长方形属性。
   • 在本题中，dp[i][j] 表示以（i,j）右下角的全由 1 构成的最大正方形边长。
   • 如果 matrix[i][j] == '1' ，那么该位置的正方形边长至少为 1 ，即 dp[i][j] = 1 ，接着考虑它是否能和左边、上边、左上角的元素构成更大的正方形。如果其他三个元素在 matrix 中也都为 1，则说明可以构成更大的正方形。
   • 假设 dp[i][j] = k ，其充分条件是 dp[i-1][j] 、dp[i-1][j-1]、dp[i][j-1] 的值必须都不小于 k -1， 否则 （i,j）位置不可能构成面积为 k² 的正方形。同理，如果这三个值中的最小值为 k-1 ，那么（i,j）位置一定能构成面积为 k² 的正方形。因此边长就可以更新为 dp[i][j] = min(min(dp[i-1][j],dp[i][j-1]), dp[i-1][j-1]) + 1;

2. 代码

   class Solution {
   public:
       int maximalSquare(vector<vector<char>>& matrix) {
           int m = matrix.size(), n = matrix[0].size();
           int ans = 0;
           vector<vector<int>> dp(m+1 , vector<int>(n+1, 0));
           for(int i=0; i<m; ++i){
               for(int j=0; j<n; ++j){
                   if(matrix[i][j] == '1'){
                       dp[i][j] = 1;
                       if(i>0 && j>0){
                           char x = matrix[i-1][j], y = matrix[i][j-1], l = matrix[i-1][j-1];
                           if(x == '1' && y == '1' && l == '1'){
                               dp[i][j] = min(min(dp[i-1][j],dp[i][j-1]), dp[i-1][j-1]) + 1;
                           }
                       }
                   }
                   ans = max(ans, dp[i][j]);
               }
           }
   
           return ans * ans;
       }
   };
   
   

3. 收获

   • 这道题是自己想出来的，一开始想把 dp中的第一行和第一列都置为 0，这样就不用考虑下标越界了，但是发现这样的话，我容易混淆 matrix[i-1][j-1] 和 dp[i][j] ，就还是将 dp 和 matrix 的元素一一对应，然后判断边界是否在合理的范围内。
   • 第二，我将 dp[i][j] 定义为 以（i,j）右下角的全由 1 构成的最大正方形面积，在计算时稍有些繁琐，题解是定义为边长，方便很多。