646. 最长数对链（中等）

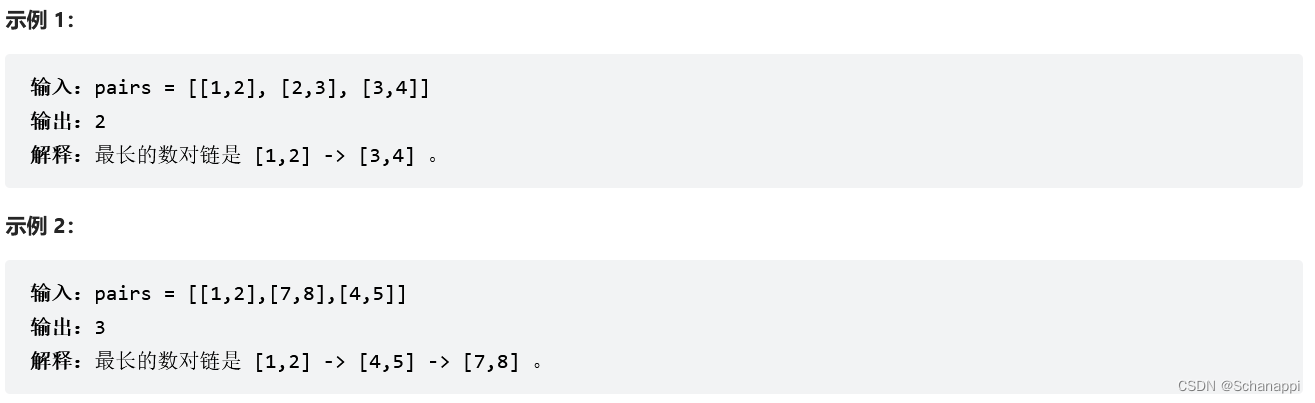
思路

这道题和 300. 最长递增子序列 类似，我们可以定义 dp 数组，其中 dp[i] 表示以 i 结尾的子序列的性质。在处理好每个位置后，统计一遍各个位置的结果即可得到题目要求的结果。

但是题目中强调了 “任何顺序选择其中的一些数对来构造”，因此我们可以先按照 right_i 对数对进行升序排序，这样能够快速判断相邻数对是否构成数对链。

状态定义

对于这道题，我们可以定义 dp[i] 为以 i 结尾的最长数对链的长度。

状态转移方程

对于每个位置 i ，如果其之前的位置 j 所对应的数对和位置 i 的数对可以构成数对链，那么我们就可以获得一个以 pairs[i] 结尾、长度为 dp[j] + 1 的更长的数对链。

初始化

对于pairs[0] ，它可以自己形成长度为 1 的数对链，所以 dp[0] = 1;。

最终的返回结果

由于 dp[i] 存储的是以 i 结尾的最长数对链的长度，而整个数对中最长数对链可能以任意其中一个元素作为结尾，所以需要遍历 dp 数组，得到最长的数对链。

即 *max_element(dp.begin(), dp.end());

代码

class Solution {
public:
    static bool cmp(vector<int>& a, vector<int>& b){
        return a[1] < b[1];
    }
    int findLongestChain(vector<vector<int>>& pairs) {
        int n = pairs.size();
        vector<int> dp(n, 0);

        sort(pairs.begin(), pairs.end(), cmp);
        // 初始化
        dp[0] = 1;

        // 状态转移方程
        for(int i=1; i<n; ++i){
            for(int j=0; j<=i; ++j){
                if(pairs[i][0] > pairs[j][1]){
                    dp[i] = max(dp[i], dp[j] + 1);
                }
                else dp[i] = max(dp[i] , 1);
            }
        }
        return *max_element(dp.begin(), dp.end());
    }
};