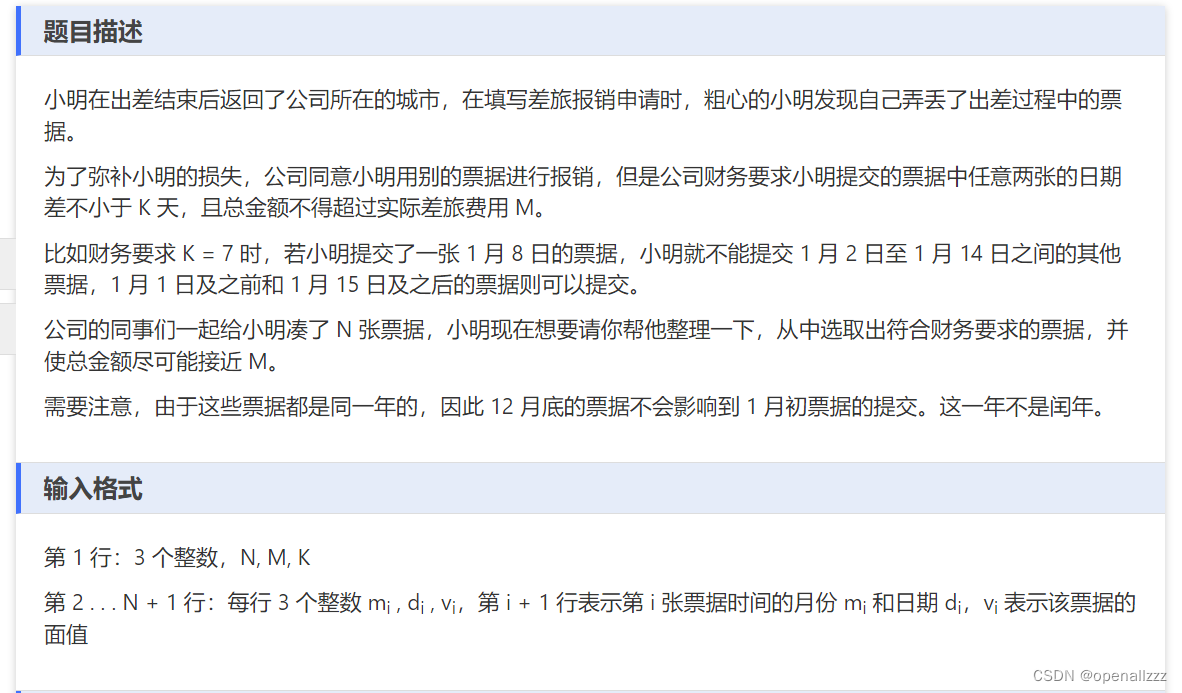
题目链接：https://www.dotcpp.com/oj/problem2696.html

思路

读完题，再看一眼数据范围，这道题的做法也就确定了——DP。

DP的题目往往很容易辨识出来，所以我们就往DP上想了，第一要素是选出的所有票据里面，任意两个票据之间相隔的天数（根据日期判断）不能小于k，这样就很直接了，我们对这些票据进行排序，根据的是它们的日期谁更小，具体的是当前日期是这一年的第x天（本年是闰年），x越小则排在越前面，这样排完序后，我们就可以进行按顺序的选取了，具体的，如果当前枚举票据i时，我们定义一个last = i - 1,这代表着：在i左边最近的满足相隔的天数不小于k的票据索引。

我们定义状态数组f[1010][5050]，f[i][j]：从前i个票据中选取若干个是否存在能凑成价值为j的方案，这样的话状态计算的就很直接了

• f[i][j] = f[i - 1][j] || (f[last][j - p[i].v])减去票据i的价值p[i].v是因为票据i在后者的表达式中代表着一定选择了第i个票据，而前者则代表着第i个票据一定不选。

思路中夹杂了代码中的变量，最好和下面的代码一起理解。

代码（C++）

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1010, M = 5010;

int days[13] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};

int get(int m, int d) {
    int res = 0;
    for(int i = 1; i < m; i ++) res += days[i];
    return res + d;
}

int n, m, k;
struct e { // 票据
    int m, d, v;
    bool operator<(e w) const {
        return get(m, d) < get(w.m, w.d);
    }
}p[N];
bool f[N][M]; // f[i][j]: 从前i个票据中选取若干个是否存在能凑成价值为j的方案

int main() {
    cin >> n >> m >> k;
    for(int i = 1; i <= n; i ++) cin >> p[i].m >> p[i].d >> p[i].v;

    sort(p + 1, p + n + 1);

    f[0][0] = true;
    for(int i = 1; i <= n; i ++) {
        int last = i - 1;
        while(last > 0 && get(p[i].m, p[i].d) - get(p[last].m, p[last].d) < k) last -- ;
        for(int j = 0; j <= m; j ++) {
            f[i][j] = f[i - 1][j];
            if(j >= p[i].v) f[i][j] |= f[last][j - p[i].v];
        }
    }

    int res = 0;
    for(int i = m; i >= 0; i --) {
        if(f[n][i]) {
            res = i;
            break;
        }
    }

    cout << res << "\n";
    return 0;
}