🔗 运行环境:matlab
🚩 撰写作者:左手の明天
🥇 精选专栏:《python》
🔥 推荐专栏:《算法研究》
#### 防伪水印——左手の明天 ####
💗 大家好🤗🤗🤗,我是左手の明天!好久不见💗
💗今天开启新的系列——重新定义matlab强大系列💗
📆 最近更新:2023 年 05 月 03 日,左手の明天的第 281 篇原创博客
📚 更新于专栏:matlab
#### 防伪水印——左手の明天 ####
目录
函数语法
B = filloutliers(A,fillmethod )
B = filloutliers(A,fillmethod ,fillmethod )
B = filloutliers(A,fillmethod ,"percentiles",threshold )
B = filloutliers(A,fillmethod ,movmethod,window)
B = filloutliers(___,dim)
B = filloutliers(___,Name,Value)
示例
在向量中对离群值进行插值
使用均值检测和最邻近值填充方法
使用移窗检测法
填充矩阵行中的离群值
指定离群值位置
返回离群值阈值
函数语法
B = filloutliers(A,fillmethod )
查找 A 中的离群值并根据 fillmethod 替换它们。例如,filloutliers(A,"previous") 将离群值替换为上一个非离群值元素。
-
如果
A是矩阵,则filloutliers分别对A的每列进行运算。 -
如果
A是多维数组,则filloutliers沿A的大小不等于 1 的第一个维度进行运算。 -
如果
A是表或时间表,则filloutliers分别对A的每个变量进行运算。
默认情况下,离群值是指与中位数相差超过三倍经过换算的 中位数绝对偏差(MAD)的值。
B = filloutliers(A,fillmethod ,fillmethod )
指定检测离群值的方法。例如,filloutliers(A,"previous","mean") 将 A 中与均值相差超过三倍标准差的元素定义为离群值。
B = filloutliers(A,fillmethod ,"percentiles",threshold )
将离群值定义为 threshold 所指定的百分位数以外的点。threshold 参数是包含上下百分位数阈值的二元素行向量,例如 [10 90]。
B = filloutliers(A,fillmethod ,movmethod,window)
使用窗长度为 window 的移动窗均值或中位数来检测局部离群值。例如,filloutliers(A,"previous","movmean",5) 将包含五个元素的窗口中与局部均值相差超过三倍局部标准差的元素标识为离群值。
B = filloutliers(___,dim)
指定 A 的运算维度。例如,filloutliers(A,"linear",2) 沿矩阵 A 的每一行运算。
B = filloutliers(___,Name,Value)
使用一个或多个名称-值参数指定用来检测和替换离群值的其他参数。例如,filloutliers(A,"previous","SamplePoints",t) 相对于时间向量 t 中的对应元素检测 A 中的离群值。
示例
在向量中对离群值进行插值
使用 "linear" 方法填充数据向量中的离群值,并可视化填充的数据。
创建一个包含两个离群值的数据向量。
A = [57 59 60 100 59 58 57 58 300 61 62 60 62 58 57];使用线性插值替换离群值。
B = filloutliers(A,"linear");绘制原始数据和填充了离群值的数据。
plot(A)
hold on
plot(B,"o-")
legend("Original Data","Filled Data")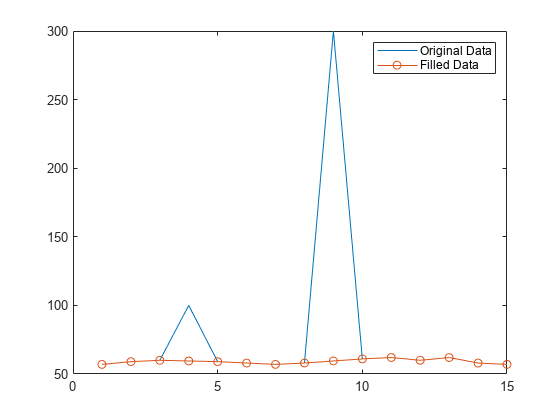
使用均值检测和最邻近值填充方法
识别数据表中的潜在离群值,使用 "nearest" 填充方法填充任何离群值,并可视化清洗后的数据。
创建一个数据时间表,并可视化数据以检测潜在的离群值。
T = hours(1:15);
V = [57 59 60 100 59 58 57 58 300 61 62 60 62 58 57];
A = timetable(T',V');
plot(A.Time,A.Var1)填充数据中的离群值,其中离群值定义为偏离均值超过三倍标准差的值。将离群值替换为最接近的非离群值元素。
B = filloutliers(A,"nearest","mean")B=15×1 timetable
Time Var1
_____ ____
1 hr 57
2 hr 59
3 hr 60
4 hr 100
5 hr 59
6 hr 58
7 hr 57
8 hr 58
9 hr 61
10 hr 61
11 hr 62
12 hr 60
13 hr 62
14 hr 58
15 hr 57
在同一个图中,绘制原始数据和填充了离群值的数据。
hold on
plot(B.Time,B.Var1,"o-")
legend("Original Data","Filled Data")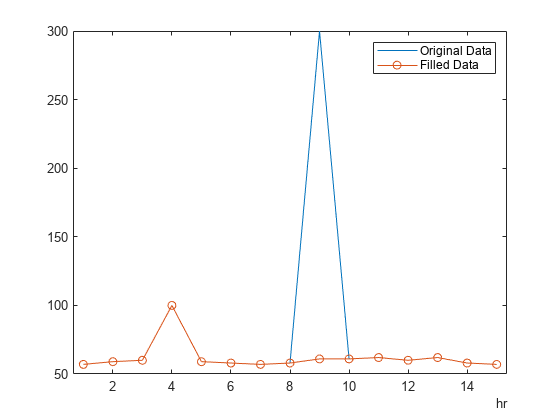
使用移窗检测法
使用移动中位数,检测并填充与时间向量对应的正弦波内的局部离群值。
创建包含一个局部离群值的数据向量。
x = -2*pi:0.1:2*pi;
A = sin(x);
A(47) = 0;创建与 A 中的数据对应的时间向量。
t = datetime(2017,1,1,0,0,0) + hours(0:length(x)-1);将离群值定义为滑动窗内与局部中位数相差超过三倍局部换算 MAD 的点。在 A 中查找与 t 中的点对应的离群值的位置,窗口大小为 5 小时。使用 "clip" 方法,用计算的阈值填充离群值。
[B,TF,L,U,C] = filloutliers(A,"clip","movmedian",hours(5),"SamplePoints",t);绘制原始数据和填充了离群值的数据。
plot(t,A)
hold on
plot(t,B,"o-")
legend("Original Data","Filled Data")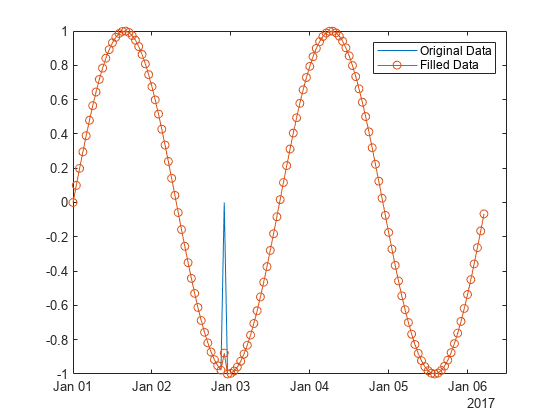
填充矩阵行中的离群值
创建一个数据矩阵,其对角线上包含离群值。
A = randn(5,5) + diag(1000*ones(1,5))A = 5×5
103 ×
1.0005 -0.0013 -0.0013 -0.0002 0.0007
0.0018 0.9996 0.0030 -0.0001 -0.0012
-0.0023 0.0003 1.0007 0.0015 0.0007
0.0009 0.0036 -0.0001 1.0014 0.0016
0.0003 0.0028 0.0007 0.0014 1.0005
基于每一行中的数据用零填充替换离群值,然后显示新值。
[B,TF] = filloutliers(A,0,2);
BB = 5×5
0 -1.3077 -1.3499 -0.2050 0.6715
1.8339 0 3.0349 -0.1241 -1.2075
-2.2588 0.3426 0 1.4897 0.7172
0.8622 3.5784 -0.0631 0 1.6302
0.3188 2.7694 0.7147 1.4172 0
可以使用 TF 作为索引向量,访问检测到的离群值及其填充的值。
[A(TF) B(TF)]ans = 5×2
103 ×
1.0005 0
0.9996 0
1.0007 0
1.0014 0
1.0005 0
指定离群值位置
创建一个包含两个离群值的向量,并检测这些离群值的位置。
A = [57 59 60 100 59 58 57 58 300 61 62 60 62 58 57];
detect = isoutlier(A)detect = 1x15 logical array 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0
使用 "nearest" 方法填充离群值。不使用检测方法,而是提供由 isoutlier 检测到的离群值位置。
B = filloutliers(A,"nearest","OutlierLocations",detect)B = 1×15
57 59 60 59 59 58 57 58 61 61 62 60 62 58 57
返回离群值阈值
使用 "clip" 填充方法替换数据向量中的离群值。
创建一个包含一个离群值的数据向量。
A = [60 59 49 49 58 100 61 57 48 58];使用默认方法 "median" 检测离群值,使用 "clip" 填充方法用上阈值替换该离群值。
[B,TF,L,U,C] = filloutliers(A,"clip");绘制原始数据、填充了离群值的数据以及由离群值检测方法确定的阈值和中心值。中心值是数据的中位数,上阈值和下阈值分别高于和低于中位数三倍换算 MAD。
plot(A)
hold on
plot(B,"o-")
yline([L U C],":",["Lower Threshold","Upper Threshold","Center Value"])
legend("Original Data","Filled Data")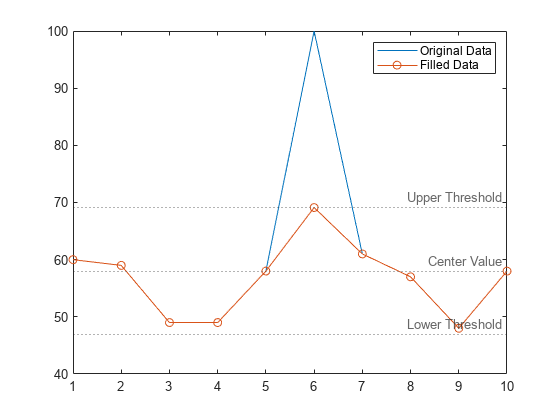
#### 防伪水印——左手の明天 ####
💗 大家好🤗🤗🤗,我是左手の明天!好久不见💗
💗今天开启新的系列——重新定义matlab强大系列💗
📆 最近更新:2023 年 05 月 03 日,左手の明天的第 281 篇原创博客
📚 更新于专栏:matlab
#### 防伪水印——左手の明天 ####