回溯
回溯是 DFS 中的一种技巧。回溯法采用 试错 的思想,它尝试分步的去解决一个问题。在分步解决问题的过程中,当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候,它将取消上一步甚至是上几步的计算,再通过其它的可能的分步解答再次尝试寻找问题的答案。
通俗上讲,回溯是一种走不通就回头的算法。
回溯的本质是穷举所有可能,尽管有时候可以通过剪枝去除一些根本不可能是答案的分支, 但是从本质上讲,仍然是一种暴力枚举算法。
回溯法可以抽象为树形结构,并且是是一颗高度有限的树(N 叉树)。回溯法解决的都是在集合中查找子集,集合的大小就是树的叉树,递归的深度,构成树的高度。
以求数组 [1,2,3] 的子集为例:
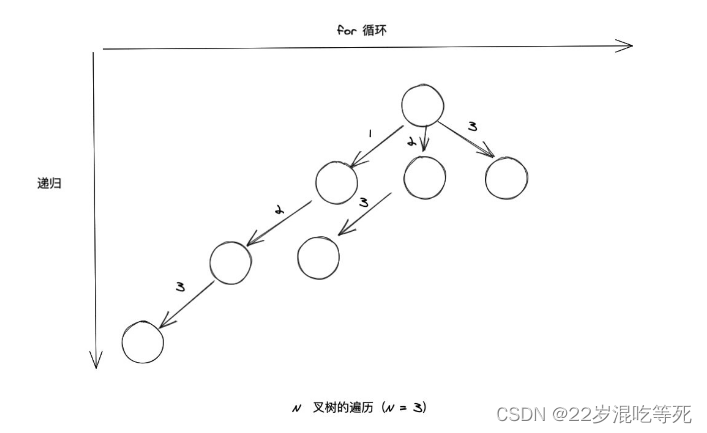
for 循环用来枚举分割点,其实区间 dp 分割区间就是类似的做法
以上图来说, 我们会在每一个节点进行加入到结果集这一次操作。
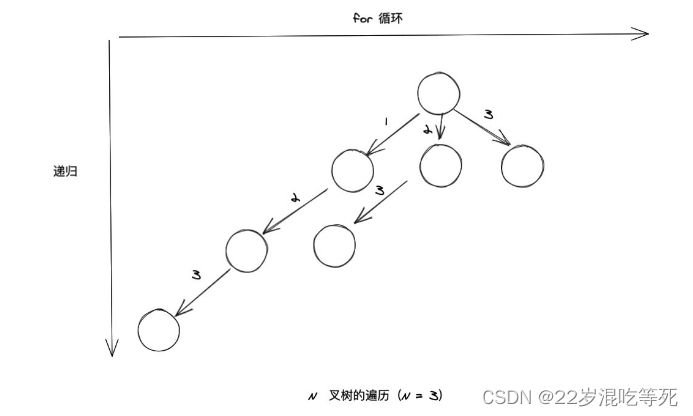
对于上面的灰色节点, 加入结果集就是 [1]。
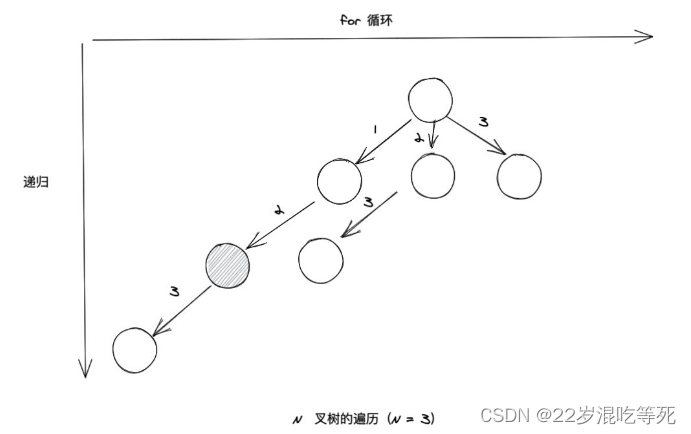
这个加入结果集就是 [1,2]。
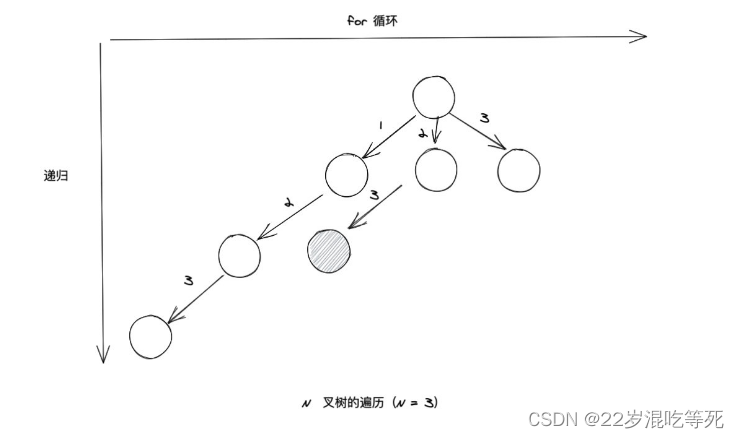
而对于全排列问题则会在叶子节点加入到结果集,不过这都是细节问题。掌握了思想之后, 大家再去学习细节就会事半功倍。
下面我们来看下具体代码怎么写。
算法流程
伪代码:
const visited = {}
function dfs(i) {
if (满足特定条件){
// 返回结果 or 退出搜索空间
}
visited[i] = true // 将当前状态标为已搜索
dosomething(i) // 对i做一些操作
for (根据i能到达的下个状态j) {
if (!visited[j]) { // 如果状态j没有被搜索过
dfs(j)
}
}
undo(i) // 恢复i
}
剪枝
回溯题目的另外一个考点是剪枝, 通过恰当地剪枝,可以有效减少时间,比如我通过剪枝操作将石子游戏 V的时间从 900 多 ms 优化到了 500 多 ms。
剪枝在每道题的技巧都是不一样的, 不过一个简单的原则就是避免根本不可能是答案的递归。
举个例子: 842. 将数组拆分成斐波那契序列
题目描述:
给定一个数字字符串 S,比如 S = "123456579",
我们可以将它分成斐波那契式的序列 [123, 456, 579]。
形式上,斐波那契式序列是一个非负整数列表 F,且满足:
0 <= F[i] <= 2^31 - 1,(也就是说,每个整数都符合 32 位有符号整数类型);
F.length >= 3;
对于所有的0 <= i < F.length - 2,都有 F[i] + F[i+1] = F[i+2] 成立。
另外,请注意,将字符串拆分成小块时,每个块的数字一定不要以零开头,除非这个块是数字 0 本身。
返回从 S 拆分出来的任意一组斐波那契式的序列块,如果不能拆分则返回 []。
示例 1:
输入:"123456579"
输出:[123,456,579]
示例 2:
输入: "11235813"
输出: [1,1,2,3,5,8,13]
示例 3:
输入: "112358130"
输出: []
解释: 这项任务无法完成。
示例 4:
输入:"0123"
输出:[]
解释:每个块的数字不能以零开头,因此 "01","2","3" 不是有效答案。
示例 5:
输入: "1101111"
输出: [110, 1, 111]
解释: 输出 [11,0,11,11] 也同样被接受。
提示:
1 <= S.length <= 200
字符串 S 中只含有数字。
还是直接套回溯模板即可解决。但是如果不进行合适地剪枝,很容易超时,这里我进行了四个剪枝操作,具体看代码。
class Solution:
def splitIntoFibonacci(self, S: str) -> List[int]:
def backtrack(start, path):
# 剪枝1
if len(path) > 2 and path[-1] != path[-2] + path[-3]:
return []
if start >= len(S):
if len(path) > 2:
return path
return []
cur = 0
ans = []
# 枚举分割点
for i in range(start, len(S)):
# 剪枝2
if i > start and S[start] == '0':
return []
cur = cur * 10 + int(S[i])
# 剪枝3
if cur > 2**31 - 1:
return []
path.append(cur)
ans = backtrack(i + 1, path)
# 剪枝 4
if len(ans) > 2:
return ans
path.pop()
return ans
return backtrack(0, [])
剪枝过程用图表示就是这样的:
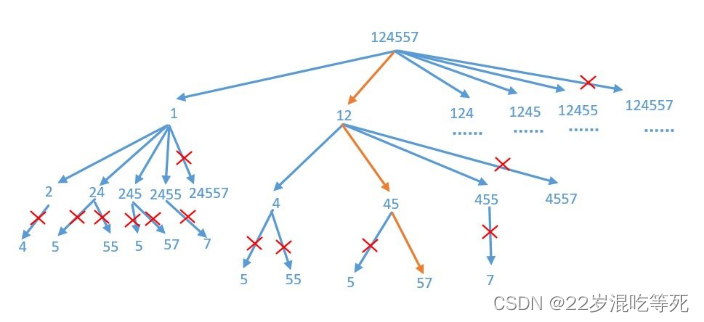
剪枝算法回溯的一大考点,大家一定要掌握。
笛卡尔积
一些回溯的题目,我们仍然也可以采用笛卡尔积的方式,将结果保存在返回值而不是路径中,这样就避免了回溯状态,并且由于结果在返回值中,因此可以使用记忆化递归, 进而优化为动态规划形式。
参考题目:

这类问题不同于子集和全排列,其组合是有规律的,我们可以使用笛卡尔积公式,将两个或更多子集联合起来。
经典题目

总结
回溯的本质就是暴力枚举所有可能。要注意的是,由于回溯通常结果集都记录在回溯树的路径上,因此如果不进行撤销操作, 则可能在回溯后状态不正确导致结果有差异, 因此需要在递归到底部往上冒泡的时候进行撤销状态。
如果你每次递归的过程都拷贝了一份数据,那么就不需要撤销状态,相对地空间复杂度会有所增加。