激活函数
作用
f(*)称为激活函数或激励函数(Activation Function),激活函数的主要作用是完成数据的非线性变换,解决线性模型的表达、分类能力不足的问题;如果网络中都是线性变换,则多层网络可以通过矩阵变换,直接转换成一层神经网络。所以激活函数的存在使得神经网络的多层可以学习更加复杂的东西,以及表示输入与输出之间的非线性的复杂任意函数映射。
激活函数另外一个作用是执行数据归一化,将输入数据映射到某个范围内再往下传递,这样可以限制数据扩张防止数据过大导致溢出。
性质
激活函数需要具有哪些性质呢?
- 1.可微性
当优化方法基于梯度的时候,这个性质是必须的
- 2.单调性
当激活函数是单调的时候,单层网络能保证是凸函数
- 3.输出值的范围
当激活函数输出值是有限的时候,基于梯度的优化方法会更加稳定,因为特征的表示受到有限权值的影响更为显著;
当激活函数的输出是无限的时候,模型的训练会更加高效,不过这种情况一般需要更小的learning rate。
从目前来看,常见的激活函数多为分段线性和具有指数形状的非线性函数。
常见激活函数
激活函数可以分为两大类:
- 饱和激活函数:sigmoid、tanh
- 非饱和激活函数:ReLU、Leaky Relu、ELU(指数线性单元)、PReLU(参数化的ReLU)、RReLU(随机ReLU)
相对于饱和函数,非饱和激活函数的优势在于: - 非饱和激活函数才能解决很多深度神经网络(网络层数巨多)的梯度消失问题,浅层网络才能用sigmoid作为激活函数(三五层)。
- 加快收敛速度
在深度学习中,比较常用的激活函数主要有:sigmoid函数、tanh函数、ReLU函数和softmax函数。
sigmoid函数
原函数:
f
(
x
)
=
1
1
+
e
−
x
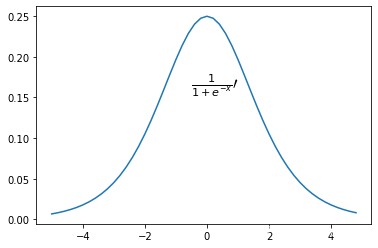
f(x)=\frac{1}{1+e^{-x}}
f(x)=1+e−x1
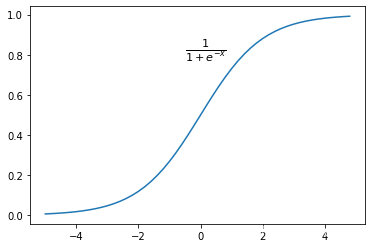
sigmoid函数导数:
f
′
(
x
)
=
(
1
1
+
e
−
x
)
′
=
e
−
x
(
1
+
e
−
x
)
2
=
e
−
x
−
1
(
1
+
e
−
x
)
2
=
(
1
1
+
e
−
x
)
(
1
−
1
1
+
e
−
x
)
=
f
(
x
)
(
1
−
f
(
x
)
)
\begin{align} f\prime(x)&=(\frac{1}{1+e^{-x}})\prime \\ &=\frac{e^{-x}}{(1+e^{-x})^{2}}\\ &=\frac{e^{-x}-1}{(1+e^{-x})^2}\\ &=(\frac{1}{1+e^{-x}})(1-\frac{1}{1+e^{-x}}) &=f(x)(1-f(x)) \end{align}
f′(x)=(1+e−x1)′=(1+e−x)2e−x=(1+e−x)2e−x−1=(1+e−x1)(1−1+e−x1)=f(x)(1−f(x))
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1/(1+np.exp(-x))
def sigmoid_prime(x):
return(sigmoid(x)*(1-sigmoid(x)))
x = np.arange(-5., 5., 0.2)
y = sigmoid(x)
plt.text(-0.5,0.8,r'$\frac{1}{1+e^{-x}}$',fontdict={'size':'16','color':'black'})
plt.plot(x, y)
y2=sigmoid_prime(x)
plt.text(-0.5,0.16,r'$\frac{1}{1+e^{-x}}\prime$',fontdict={'size':'16','color':'black'})
plt.plot(x, y2)
作用
Sigmoid 是以前最常用的非线性的激活函数,它能够是把输入的 (-∞,+∞)范围内 连续实值变换为0和1之间的输出,特别的,如果是非常大的负数,那么输出就是0;如果是非常大的正数,输出就是1。
优点
- 1.输出范围有限,数据传递过程中不容易发散
- 2.导数容易计算
缺点 - 1.输出范围有限也会导致饱和的时候梯度太小
- 2.深度神经网络中梯度反向传递时导致梯度爆炸或梯度小时,其中梯度爆炸发现概率较小,梯度消失发生概率较大
- 3.sigmoid的output不是0均值(zero-centered),这会导致后一层的神经元得到上一层输出的非零均值的信号作为输入
- 解析式中含有幂运算,计算机求解相对耗时
优点
- 在特征相差明显的情况下效果会很好,因为该激活函数会在循环过程中不断扩大特征效果
tanh函数
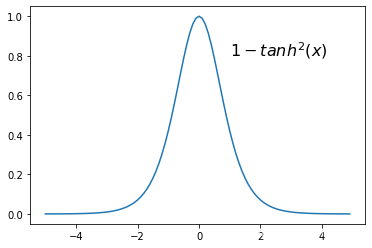
双曲正切函数(Hyperbolic tangent function),将一个 (-∞,+∞)范围内 实值输入压缩至 [-1, 1]的范围,这类函数具有平滑和渐近性,并保持单调性。
它解决了Sigmoid函数的不是zero-centered输出问题,与sigmoid相比,它的输出均值是0,使得其收敛速度要比sigmoid快,减少迭代次数,然而,梯度消失(gradient vanishing)的问题和幂运算的问题仍然存在。
tanh函数本质上是sigmoid函数的变形: t a n h ( x ) = 2 S i g m o i d ( 2 x ) − 1 tanh(x)=2Sigmoid(2x)-1 tanh(x)=2Sigmoid(2x)−1
原函数:
t
a
n
h
(
x
)
=
2
S
i
g
m
o
i
d
(
2
x
)
−
1
=
s
i
n
h
x
c
o
u
s
h
x
=
e
x
−
e
−
x
e
x
+
e
−
x
\begin{align} tanh(x)&=2Sigmoid(2x)-1\\ &=\frac{sinhx}{coushx}\\ &=\frac{e^x-e^{-x}}{e^x+e^{-x}} \end{align}
tanh(x)=2Sigmoid(2x)−1=coushxsinhx=ex+e−xex−e−x
原函数求导:
首先
:
(
e
x
)
′
=
e
x
,
(
e
−
x
)
′
=
−
e
−
x
其次
:
(
u
v
)
′
=
u
′
v
−
u
v
′
v
2
t
a
n
h
(
x
)
′
=
(
e
x
+
e
−
x
)
(
e
x
−
e
−
x
)
−
(
e
x
−
e
−
x
)
(
e
x
−
e
−
x
)
(
e
x
+
e
−
x
)
2
=
1
−
(
e
x
−
e
−
x
)
2
(
e
x
+
e
−
x
)
2
=
1
−
t
a
n
h
2
(
x
)
\begin{align} 首先&:(e^x)\prime=e^x,(e^{-x})\prime=-e^{-x}\\ 其次&: \left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime} v-u v^{\prime}}{v^{2}} \\ tanh(x)\prime&=\frac{(e^x+e^{-x})(e^x-e^{-x})-(e^x-e^{-x})(e^x-e^{-x})}{(e^x+e^{-x})^{2}}\\ &=1-\frac{(e^x-e^{-x})^2}{(e^x+e^{-x})^{2}}\\ &=1-tanh^2(x) \end{align}
首先其次tanh(x)′:(ex)′=ex,(e−x)′=−e−x:(vu)′=v2u′v−uv′=(ex+e−x)2(ex+e−x)(ex−e−x)−(ex−e−x)(ex−e−x)=1−(ex+e−x)2(ex−e−x)2=1−tanh2(x)
![[attachments/tanh导数函数图像.png]]
import numpy as np
import matplotlib.pyplot as plt
def tanh(x):
return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
def tanh_prime(x):
return 1-tanh(x)*tanh(x)
x = np.arange(-5., 5., 0.1)
y = tanh(x)
plt.text(-0.5,0.8,r'$\frac{e^x-e^{-x}}{e^x+e^{-x}}$',fontdict={'size':'16','color':'black'})
plt.plot(x, y)
y2=tanh_prime(x)
plt.text(1,0.8,r'$1-tanh^2(x)$',fontdict={'size':'16','color':'black'})
plt.plot(x, y2)
Relu函数
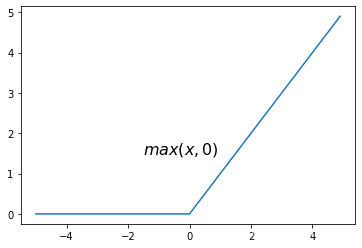
ReLU(Rectified Linear Unit), 修正线性单元- 用于隐层神经元输出, 深度学习目前最常用的激活函数,是一种分段线性函数,弥补了sigmoid函数以及tanh函数的梯度消失问题。
原函数:
ϕ
(
x
)
=
m
a
x
(
0
,
x
)
\phi(x)=max(0,x)
ϕ(x)=max(0,x)
其导函数

def ReLU(x):
x2 = (np.abs(x) + x) / 2.0
return x2
def ReLU_prime(x):
return np.where(x > 0, 1, 0)
x = np.arange(-5., 5., 0.1)
y = [0]*len(x)
print (x)
plt.text(-1.5,1.5,r'$max(x,0)$',fontdict={'size':'16','color':'black'})
Y=ReLU(x)
plt.plot(x, Y)
print(x)
y2=ReLU_prime(x)
plt.text(1,0.8,r'$max(x,0)\prime$',fontdict={'size':'16','color':'black'})
print(y2)
plt.plot(x, y2)
优点
- 在正区间解决了梯度消失(gradient vanishing)问题
- 计算速度快
- 使用梯度下降法的时候收敛速度快
缺点 - 输出不是zero-centered
- Dead ReLU Problem,指的是某些神经元可能永远不会被激活,导致相应的参数永远不能被更新。有两个主要原因可能导致这种情况产生: (1) 非常不幸的参数初始化,这种情况比较少见 (2) learning rate太高导致在训练过程中参数更新太大,不幸使网络进入这种状态。解决方法是可以采用Xavier初始化方法,以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。
Softmax函数
Softmax用于多分类神经网络输出,Softmax可以将数值向量转换成概率分布,Sigmod是Softmax函数的一个特例,Sigmod函数只能预测值为0或者1的二元分类。
原函数:
y
k
=
e
a
k
∑
i
=
1
n
e
a
i
y_k=\frac{e^{a_k}}{\sum\limits_{i=1}^{n}e^{a_i}}
yk=i=1∑neaieak
上式表示假设输出层共有 n 个神经元,计算第 k 个神经元的输出 y k y_{k} yk。如上式所示,softmax 函数的分子是输入信号 a k a_{k} ak的指数函数,分母是所有输入信号的指数函数的和。
@未完
def softmax(x):
return np.exp(x) / np.sum(np.exp(x))
对于长度为 K 的任意实向量,Softmax函数可以将其压缩为长度为 K,值在 [0,1] 范围内,并且向量中元素的总和为 1 的实向量。 Softmax函数与正常的max函数不同:max函数仅输出最大值,但Softmax函数确保较小的值具有较小的概率,并且不会直接丢弃。我们可以认为它是arg max函数的概率版本或“soft”版本。Softmax函数的分母结合了原始输出值的所有因子,这意味着Softmax函数获得的各种概率彼此相关。
特点
- 在零点不可微。
- 负输入的梯度为零,这意味着对于该区域的激活,权重不会在反向传播期间更新,因此会产生永不激活的死亡神经元。
total
| 激活函数 | 特点 | 缺点 | 优点 |
|---|---|---|---|
| Sigmoid | 导数易得,以前常用 | 梯度消失、非零均值、计算耗时 | |
| tanh | 解决了Sigmoid零均值问题 | 梯度消失、计算耗时 | 收敛更快 |
| Relu | 解决了梯度消失问题 | 非零均值、死神经 | 梯度下降收敛快 |
| Softmax | 多分类问题,向量转概率 |
@未完
参考
神经网络中的激活函数有什么作用 - 知乎 (zhihu.com)
神经网络激活函数的作用是什么? - 知乎 (zhihu.com)
谈谈激活函数以零为中心的问题 | 始终 (liam.page)
(30条消息) 【深度学习】:超详细的Softmax求导_BQW_的博客-CSDN博客_softmax的导数
(30条消息) 机器学习中的数学——激活函数(四):Leaky ReLU函数_von Neumann的博客-CSDN博客_leakyrelu激活函数