不确定性

不确定性与理性决策

基本概率符号

先验概率(无条件概率)/后验概率(条件概率)

随机变量

概率密度

联合概率分布

公理

完全联合分布

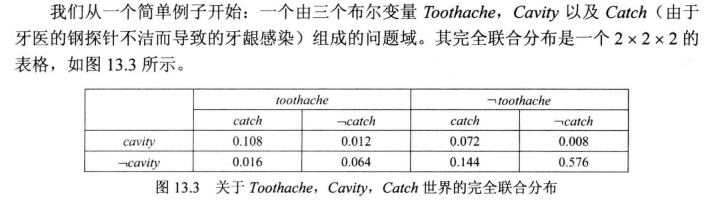
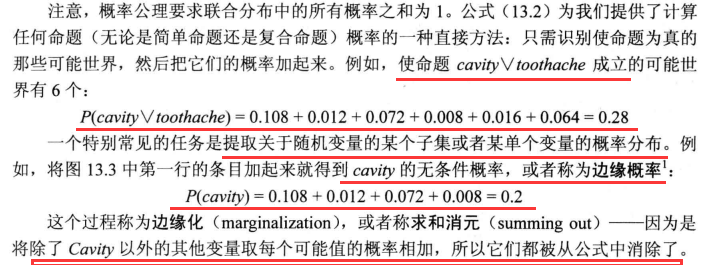
概率演算

独立性

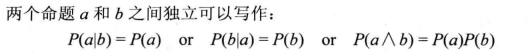
贝叶斯法则

例1

你有两个信封可供选择。一个信封里有一个红球（价值100美元）和一个黑球，另一个信封里有两个黑球（价值为零）。

你随机选择一个信封，然后从该信封中随机取出一个球，结果是黑色的。

此时，你可以选择是否换另一个信封。问题是，你应该换还是不换？

---

E: envelope, 1表示有一个红球的信封，2表示都是黑球的信封$1=(R,B),2=(B,B)$

B: the event of drawing a black ball 拿到一个黑棋的事件

$$\begin{gathered} 贝叶斯法则： \\ P(E|B)=\frac{P(B|E)P(E)}{P(B)} \end{gathered}$$

We want to compare $比较：P(E=1|B)$ vs. $P(E=2|B)$

$$\begin{gathered} 在红球信封拿到黑球：P(B|E=1)=0.5 \\ 在黑球信封拿到黑球：P(B|E=2)=1 \end{gathered}$$

$$拿到1、2信封的概率相同：P(E=1)=P(E=2)=0.5$$

$$\begin{array}{rl}& 抽到黑球的概率：\\ & B在E取值上的边缘概率\\ P(B)& =P(B|E=1)P(E=1)+P(B|E=2)P(E=2)\\ & =(0.5)(0.5)+(1)(0.5)\\ & =0.75\end{array}$$

$$\begin{gathered} 已经抽到一个黑球，此信封是红球信封的概率： \\ P(E=1|B)=\frac{P(B|E=1)P(E=1)}{P(B)}=\frac{(0.5)(0.5)}{(0.75)}=\frac{1}{3} \end{gathered}$$

$$\begin{gathered} 已经抽到一个黑球，此信封是黑球信封的概率： \\ P(E=2|B)=\frac{P(B|E=2)P(E=2)}{P(B)}=\frac{(1)(0.5)}{(0.75)}=\frac{2}{3} \end{gathered}$$
$$\begin{gathered} 通过计算可得，抽到黑球后信封为1的概率为1/3， \\ 信封为2的概率为2/3。因此，更换信封可以提高获得红球的概率。 \end{gathered}$$

---

例2

一位医生进行一项测试，该测试有99%的可靠性，即99%的生病者测试结果为阳性，99%的健康者测试结果为阴性。这位医生估计整个人口中有1%的人是生病的。
因此，对于测试结果为阳性的患者，他是生病的概率是多少呢？

---

我们可以使用贝叶斯定理来计算患者生病的条件概率。设事件 S 表示患者生病，事件 T 表示测试结果为阳性。则所求的条件概率为：

$$P(S|T)=\frac{P(T|S)P(S)}{P(T)}$$

其中，$P(T|S)$ 表示患者生病的条件下，测试结果为阳性的概率，$P(S)$ 表示患者生病的先验概率，$P(T)$ 表示测试结果为阳性的概率。

$$\begin{gathered} 根据题目中给出的数据，我们有： \\ P(T|S)=0.99 \end{gathered}$$
$$P(S)=0.01$$
$$P(T)=P(T|S)P(S)+P(T|\overline{S})P(\overline{S})$$

$$其中，\overline{S}表示患者不生病。$$

$$\begin{gathered} 根据测试的可靠性，我们可以得到 \\ P(T|\overline{S})=1-P(T|S)=0.01 \\ 因此 \\ \begin{array}{rl}P(T)& =P(T|S)P(S)+P(T|\overline{S})P(\overline{S})\\ & =(0.99)(0.01)+(0.01)(0.99)\\ & =0.0198\end{array} \end{gathered}$$

$$\begin{gathered} 代入贝叶斯公式，我们可以计算出患者生病的条件概率： \\ P(S|T)=\frac{(0.99)(0.01)}{0.0198}\approx 0.50 \\ 因此，测试结果为阳性的患者生病的概率约为50 \end{gathered}$$

---

使用贝叶斯规则：合并证据

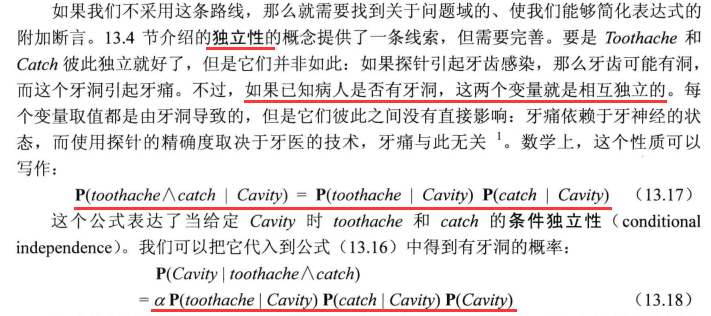
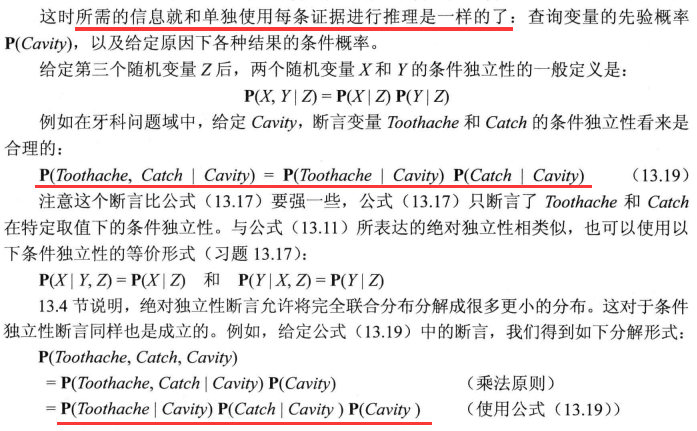
朴素贝叶斯

最大似然估计

最大似然估计（Maximum Likelihood Estimation，简称MLE）是一种常用的参数估计方法，用于根据已知的样本数据来估计模型的参数。它的核心思想是选择能够使观测到的数据出现的概率最大的参数作为估计值。

具体来说，在最大似然估计中，我们假设样本数据来自于某个概率分布，但是该分布的参数是未知的。我们的目标是通过样本数据来估计这些参数，使得该分布能够最好地解释观测到的数据。

假设我们有一个样本集合 $X=x_1,x_2,...,x_n$，每个样本都是来自于某个分布 $f(x|\theta )$ 的观测值，其中 $\theta$ 是分布的参数。我们要找到能够最大化样本集合 $X$ 的联合概率密度函数 $L(X|\theta )$ 的参数值 $\theta$。这个联合概率密度函数可以表示为：

$$L(X|\theta )=\prod _{i=1}^{n}f(x_i|\theta )$$

我们的目标是找到能够最大化 $L(X|\theta )$ 的 $\theta$ 值。因此，最大似然估计的计算可以表示为：

$${\hat{\theta }}_{MLE}=\arg \underset{\theta }{\max }L(X|\theta )$$

有时候我们需要对上式取对数来避免计算机计算下溢，得到的式子为：

$${\hat{\theta }}_{MLE}=\arg \underset{\theta }{\max }\log L(X|\theta )=\arg \underset{\theta }{\max }\sum _{i=1}^n\log f(x_i|\theta )$$

最大似然估计方法是一种常用的参数估计方法，具有计算简单、理论基础好等优点。它在统计学、机器学习、信号处理等领域都得到了广泛应用。

小结

以下是对概率论中重要的公式的整理：

---

1. 条件概率公式：

对于事件 A 和事件 B，其条件概率表示为 $P(A|B)$，表示在事件 B 发生的条件下，事件 A 发生的概率。条件概率公式为：

$$P(A|B)=\frac{P(A,B)}{P(B)}$$

---

2. 乘法规则公式：

对于事件 A 和事件 B，其联合概率表示为 $P(A,B)$，表示事件 A 和事件 B 同时发生的概率。乘法规则公式为：

$$P(A,B)=P(A|B)P(B)$$

---

3. 链式规则公式：

对于多个事件 $A,B,C,D$，其联合概率表示为 $P(A,B,C,D)$，链式规则公式可以表示为：

$$P(A,B,C,D)=P(A|B,C,D)P(B|C,D)P(C|D)P(D)$$

---

4. 条件化的链式规则公式：

对于事件 A 和事件 B，其联合概率表示为 $P(A,B)$，条件化的链式规则公式可以表示为：

$$P(A,B|C)=P(A|B,C)P(B|C)$$

---

5. 贝叶斯定理公式：

贝叶斯定理是根据先验概率和条件概率来计算后验概率的一种方法，可以用于分类、预测等任务。贝叶斯定理公式为：

$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$

---

6. 条件化的贝叶斯定理公式：

对于事件 A 和事件 B，条件化的贝叶斯定理公式可以表示为：

$$P(A|B,C)=\frac{P(B|A,C)P(A|C)}{P(B|C)}$$

---

7. 加法/条件概率公式：

对于事件 A 和事件 B，加法/条件概率公式可以表示为：

$$P(A)=P(A,B)+P(A,\neg B)=P(A|B)P(B)+P(A|\neg B)P(\neg B)$$

---

这些公式在概率论中非常重要，可以应用于统计学、机器学习、信号处理、金融领域、医学领域等各个领域的问题中。熟练掌握这些公式可以帮助我们更好地理解和解决实际问题。