前言
图与图的表示
图是由一些点和一些线构成的,能表示一些实体之间的关系,图中的点就是实体,线就是实体间的关系。如下图,v就是顶点,e是边,u是整张图。attrinbutes是信息的意思,每个点、每条边、每个图都是有信息的。


每个顶点、边和整张图都可以用一个向量来表示,在这个例子中,顶点的向量有六个值,柱体的高矮就表示该值的大小,每条边用一个长为8的向量来表示,全局用一个长为5的向量来表示
转换成图的信息表示


神经网络与图的挑战
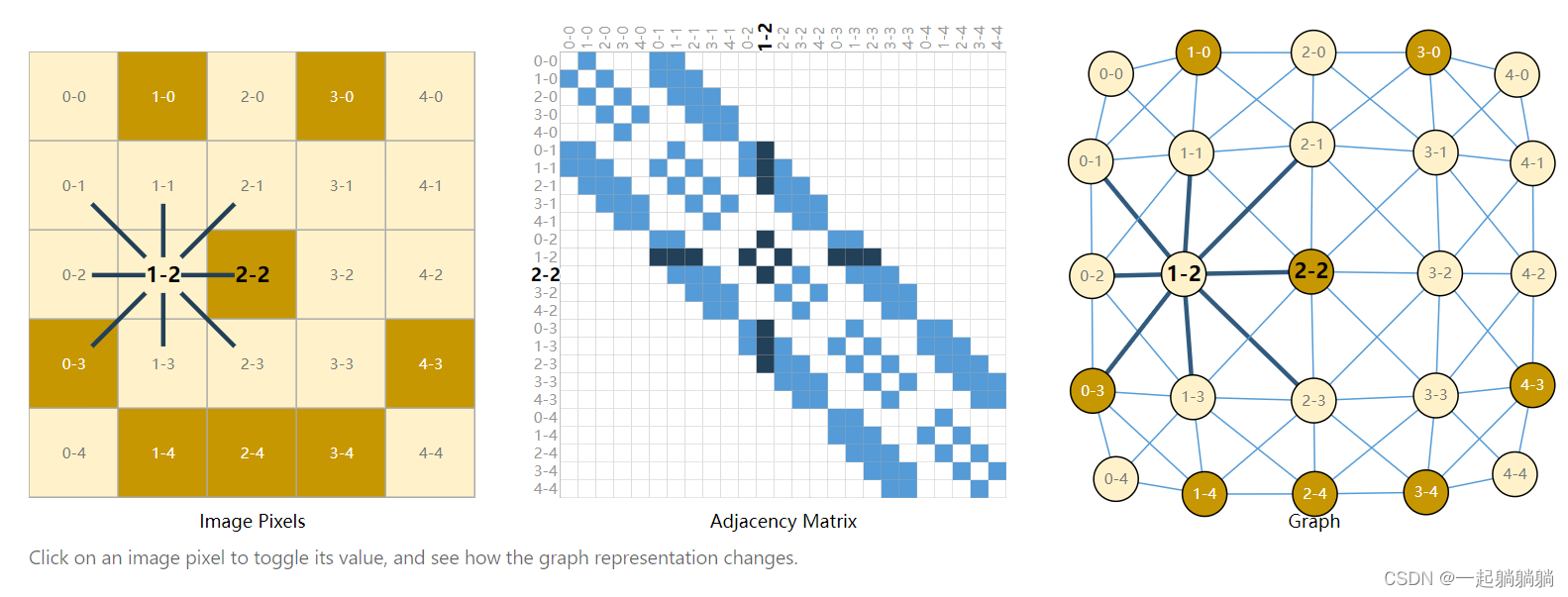
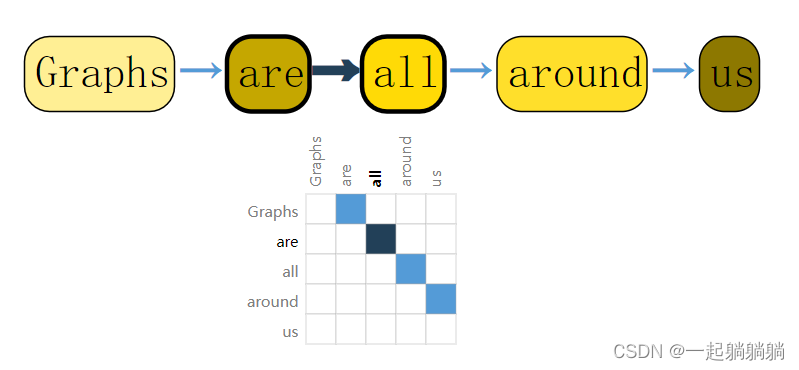
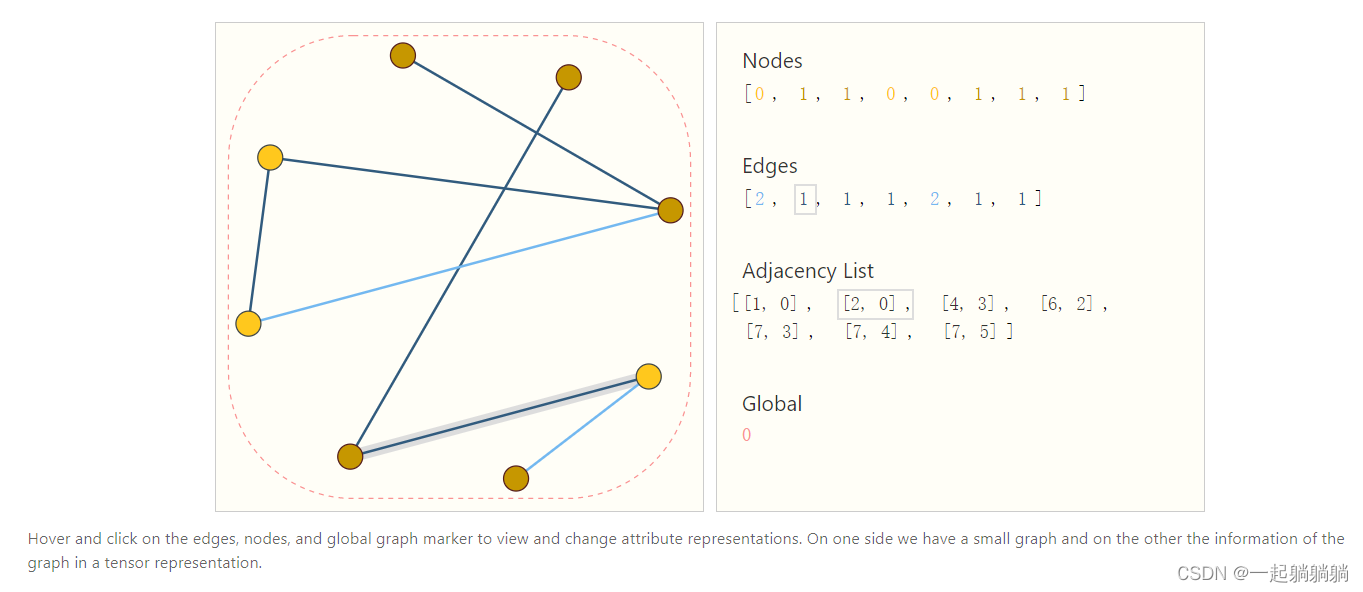
核心问题是怎样表示图才能是和神经网络是兼容的。图上有四种信息:顶点的属性,边的属性,全局信息以及连接性(即为每条边连接的是哪两个顶点)。前三个信息都能用向量来表示,连接性可以用邻接矩阵来表示,该矩阵会是一个方阵,但是有一些问题。这个矩阵可能会非常大而且很稀疏,在空间上效率低下,并且计算比较困难。另外将邻接矩阵的行或列的顺序进行交换不会改变其属性的。 如果既想高效的存储邻接矩阵,又想这个顺序不会影响神经网络的结果,就可以用邻接链表的方式来表示邻接矩阵。

图神经网络 GNN
GNN是对保持图对称性(排列不变性)的图的所有属性(节点、边、全局上下文)的可优化转换。对称信息指的是把这个顶点进行另外一个排序后,整个结果是不会变的。
GNN的理论基础是不动点(the fixed point)理论,这里的不动点理论专指巴拿赫不动点定理(Banach's Fixed Point Theorem)。首先我们用 表示若干个 堆叠得到的一个函数,也称为全局更新函数
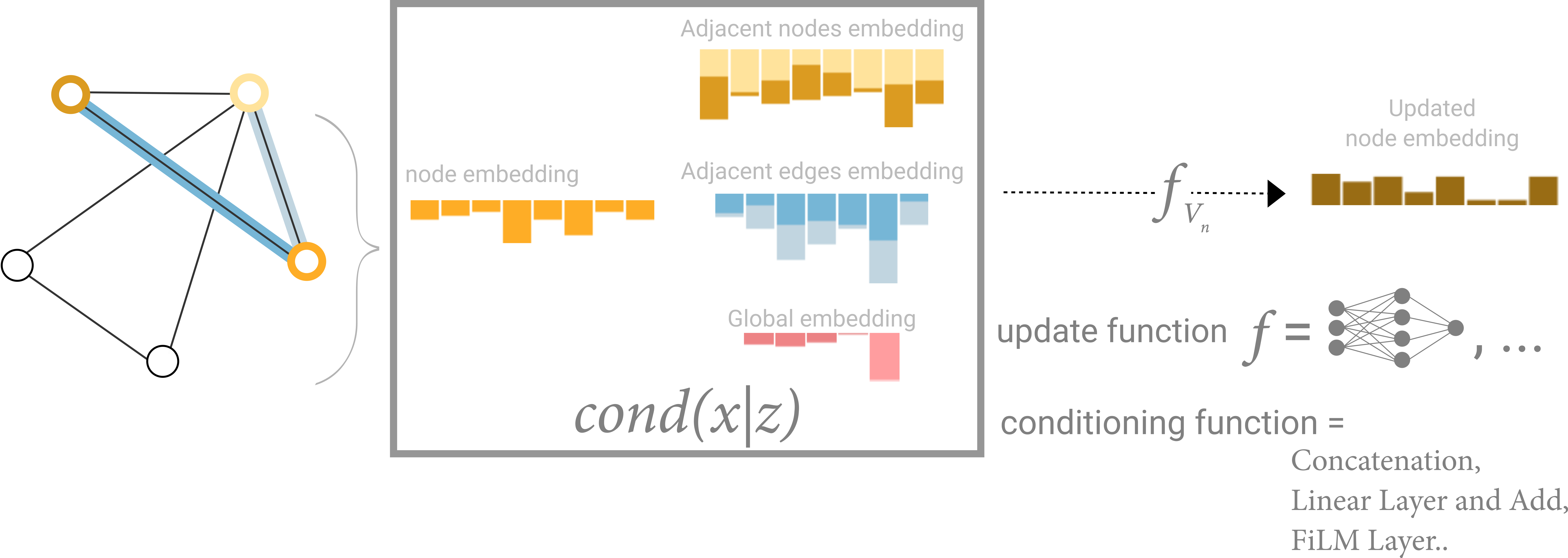
GNN更新方法

- GNN的基础理论是不动点理论,这就意味着GNN沿时间展开的长度是动态的,是根据收敛条件确定。而RNN沿时间展开的长度就等于序列本身的长度
- GNN采用 Almeida-Pineda(AP) 算法反向传播优化,而RNN使用BPTT(Back Propogation Through Time)优化。前者对收敛性有要求,而后者对收敛性是没有要求的。
- GNN循环调用 f 的目标是得到每个结点稳定的隐藏状态,所以只有在隐藏状态收敛后才能输出;而RNN的每个时间步上都可以输出,比如语言模型。
- GNN每次时间步的输入都是所有结点v的特征,而RNN每次时间步的输入是该时刻对应的输入。同时,时间步之间的信息流也不相同,前者由边决定,后者则由序列的读入顺序决定。
GNN局限
初代GNN,也就是基于循环结构的图神经网络的核心是不动点理论。它的核心观点是通过结点信息的传播使整张图达到收敛,在其基础上再进行预测。收敛作为GNN的内核,同样局限了其更广泛的使用,其中最突出的是两个问题:
- GNN只将边作为一种传播手段,但并未区分不同边的功能。虽然我们可以在特征构造阶段为不同类型的边赋予不同的特征,但相比于其他输入,边对结点隐藏状态的影响实在有限。并且GNN没有为边设置独立的可学习参数,也就意味着无法通过模型学习到边的某些特性。
- 如果把GNN应用在图表示的场景中,使用不动点理论并不合适。这主要是因为基于不动点的收敛会导致结点之间的隐藏状态间存在较多信息共享,从而导致结点的状态太过光滑(Over Smooth),并且属于结点自身的特征信息匮乏(Less Informative)。
GCN:图卷积网络(Graph Convolutional Networks)
(半监督)
ViG:Vision GNN(2022)
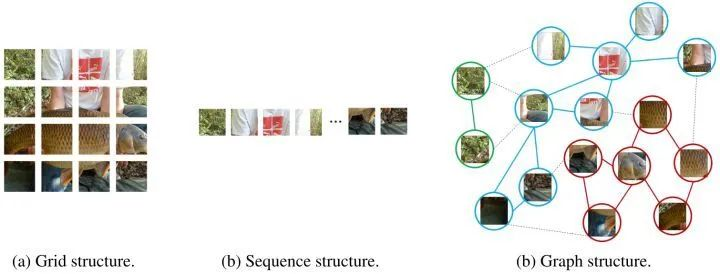
计算机视觉的一个基本任务是识别图像中的物体。由于图片中的物体通常不是形状规则的方形,所以经典的网格表示或者序列表示在处理图片时显得冗余且不够灵活。比如一个对象可以被视为由很多部分的组合:例如,一个人可以粗略地分为头部、上身、手臂和腿,这些由关节连接的部分自然形成一个图结构。
基于把图片视为图表示的观点,本文提出一种基于图表示的新型通用视觉架构 ViG。将输入图像分成许多小块,并将每个小块视为图中的一个节点。在构建好了输入图片的图表征之后,作者使用 ViG 模型在所有节点之间交换信息。ViG 的基本组成单元包括两部分:用于图形信息处理的 GCN (图形卷积网络) 模块和用于节点特征变换的 FFN (前馈网络) 模块。在图像识别,目标检测等视觉任务中证明了该方法的有效性。
图片的图表示 (Graph Representation)
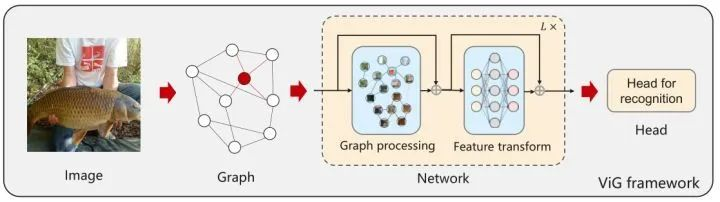
图神经网络学习框架(2020)

图神经网络应用

References
图神经网络简介,什么是图神经网络,GNN_一起躺躺躺的博客-CSDN博客_图神经网络
数学公式:图神经网络GNN教程:7篇带你彻底学习 - 知乎
几种图神经网络方法总结(Graph Neural Network)_图灵的喵的博客-CSDN博客_图神经网络
表示符号和一些模型:【图神经网络综述】一文道尽GNN原理、框架和应用 - 飞桨AI Studio
GNN起源:图系列|从图(Graph)到图卷积(Graph Convolution): 漫谈图神经网络模型(一)